3.2. Классификация типов разрушения.

Как правило, разрушение композиционных материалов инициируется в матрице или на границе раздела «матрица-упрочнитель». По размеру d зоны (3) – (область у вершины трещины, в которой при нагружении силой F, приложенной к берегам трещины, может проявиться пластическая деформация),

Рис. 3.7. Схематические изображения образования зародышевой микротрещины (2).

а – у границы зерна (1),

б – в пересекающихся плоскостях скольжения (5),

в – у вершины дислокационного скопления (6),

3 – скопление дислокаций,

4 – головные дислокации,

Э¹-Э⁷ – экстраплоскости дислокаций,

_с – направление действия сжимающих напряжений.

разрушение матрицы предложено классифицировать по 3 типам (рис.3.8):

1) хрупкое (d=0), характерное для широкого класса керамических материалов;

2) вязкое (d), присущее весьма пластичным металлам, например свинцу, а также некоторым видам пластмасс;

3) квази-хрупкое (d>0; d), относящееся к большинству материалов, которым свойственно проявление какой-либо пластичности. Чем больше размер d указанной зоны, тем в большей степени возможно развитие процесса релаксации напряжений у вершины трещины при нагружении. Материалы с протяженной «зоной пластичности» способны оказывать повышенное сопротивление развитию трещины.

3.3. Энергетическое и силовое условие развития трещины.

Энергетическое условие развития трещины. Для того, чтобы зародившаяся в объеме кристаллического тела трещина стала распространяться, необходимо выполнение некоторого энергетического условия. Рассмотрим вклады энергий, определяющих процесс развития трещины в теле материала. Под действием внешней нагрузки, приложенной к телу, на него воздействует энергия поля приложенных напряжений – U. Если тело способно к упругой деформации, то оно, при этом, может запасать в своем объеме определенную долю энергии упругой деформации – W (это энергия, запасенная в объеме упругодеформированного тела). Сумма энергий U и W – это энергетический потенциал ( или энергетический резервуар), величина (или наполнение) которого определяет возможность (или невозможность) страгивания трещины.

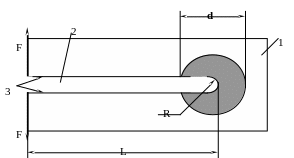
Рис. 3.8. Иллюстрация к классификации типов разрушения.

1 – матрица, 2 – трещина, 3 – берега трещины.

L – длина трещины, R= а₀/2 – радиус кривизны вершины трещины,

а₀ – расстояние между атомами в кристаллической решетке,

F –приложенная нагрузка, d –линейный размер «зоны пластичности»

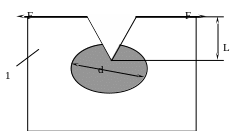
Рис. 3.9. Иллюстрация к записи энергетического условия развития трещины.

1 – матрица, L – длина трещины, F –приложенная нагрузка, d –линейный размер «зоны пластичности».

Какие энергетические составляющие противодействуют движению трещины? Это энергия пластической деформации P, развивающейся в области у вершины трещины (можно полагать, что ее доля пропорциональна размеру «зоны пластичности» - d). А также энергия, которую необходимо затратить на разрыв межатомных связей для образования двух берегов трещины (т.е. двух новых поверхностей), ее называют поверхностной энергией трещины и обозначают - . Сумма энергий Р и  противодействует распространению трещины. С учетом вышесказанного, энергетическое условие развития трещины (рис.3.9) в общем виде может быть записано следующим образом:

d/dl (U+W- Р-  )  0

1) если U+W = Р +  , то такое условие определяет состояние равновесия трещины;

2) если U+W > Р +  , то это условие определяет старт трещины.

Используя представления теории дислокаций, энергетическое условие перехода от стабильной зародышевой микротрещины к непрерывно растущей (рис.3.10) можно записать следующим образом:

n  a    2  

где: n – количество головных дислокаций в скоплении (S); а – межатомное расстояние в плоскости микротрещины (А-А) (величина а пропорциональна вектору Бюргерса n – головных дислокаций в скоплении);  - приложенное напряжение;  - поверхностная энергия

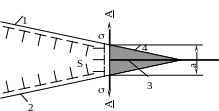
Рис. 3.10 Иллюстрация к записи энергетического условия развития трещины с позиций теории дислокаций.

 - дислокации, 1, 2 – плоскости скольжения дислокаций, 3 – плоскость развития трещины, 4 – зародышевая микротрещина, S – скопление дислокаций, а – межатомное расстояние в плоскости микротрещины (А-А),  - приложенное напряжение.

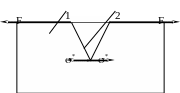
Рис. 3.11. Иллюстрация к записи силового условия развития трещины.

1 – матрица, 2 – трещина, F – приложенная нагрузка, ^* – напряжения у вершины трещины.

трещины. Это условие развития трещины в соответствии с представлениями Коттрелла: развитие трещины становится возможным, если работа, совершаемая при приложении внешнего напряжения, достаточна для создания скопления из n – головных дислокаций (с некоторым критическим значением вектора Бюргерса) и разрыва межатомных связей с образованием двух берегов трещины. Отметим, что в момент старта трещины плотность головных дислокаций достигает максимально возможного значения и появление новых дислокаций в скоплении невозможно, поскольку в данной локальной области материал теряет способность к пластической деформации (он как бы охрупчивается). В этом случае механизм сопротивления разрушению за счет релаксации приложенных напряжений в «зоне пластичности» - исчерпан. Далее приложенное внешнее напряжение будет выполнять работу по разрыву межатомных связей с образованием берегов трещины.

Силовое условие развития трещины. Представим, что некоторое тело содержит трещину (рис.3.11). Если к нему приложить внешнюю нагрузку F, то при определенном условии трещина начнет распространяться. Его можно записать в достаточно простой форме, если понять разницу в распределении напряжений, возникающих от воздействующей внешней нагрузки, в изотропном, сплошном теле и в теле, содержащим концентратор напряжений – трещину. В первом случае напряжения распределяются по всему объему материала, во втором они концентрируются вдоль вершины (кромки) трещины. При этом напряжения, возникающие у вершины трещины - ^, намного превышают номинальные - _ном, рассчитанные при растяжении изотропного, сплошного тела как отношение действующей нагрузки к площади поперечного сечения. Поэтому, исходя из общих соображений, можно записать следующие условия для равновесного состояния трещины и ее развития в тело материала:

^ = _теор. – условие состояния равновесия трещины;

^  _теор. – условие старта трещины;

где _теор. – значение теоретической прочности материала при конкретном виде нагружения (отрыв, сдвиг, кручение).