4. Разработка программы для эвм и моделирование режима работы привода
Созданная модель может быть использована для проведения исследований объекта. Ниже рассмотрен пример моделирования следящего по скорости режима работы исполнительного механизма.
Привод описывается дифференциальным уравнением 1-го порядка:
(4.1)
Для упрощения схемы моделирования вычислим постоянные величины, входящие в дифференциальное уравнение:
;
;
.
Тогда получаем:
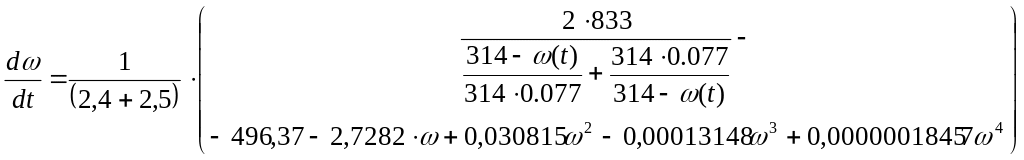(4.2)
Решая данное
нелинейное дифференциальное уравнение
с использованием программы Maple
и учитывая начальные условия
,
получаем зависимость
.
На основе полученного решения дифференциального уравнения смоделируем следящий по скорости режим работы привода.
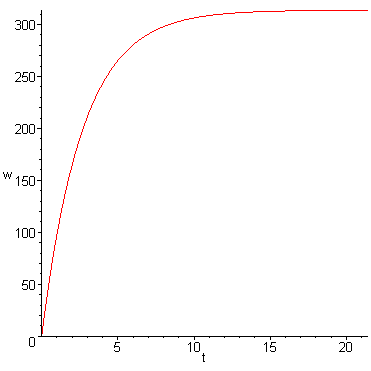
Рисунок 4 - График переходного процесса
Для моделирования
заданного режима работы привода (следящий
по скорости) зададимся значением скорости
.
Для этого в дифференциальное уравнение
математической модели введем приращение
скорости
.
В
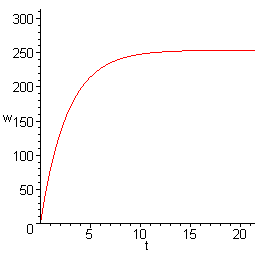
Рисунок 5 - График переходного процесса
При моделировании следящего по скорости режима работы двигателя был разработан следующий алгоритм моделирования.
Рисунок 6 – Схема алгоритма моделирования
5. Выводы и заключение
В данном курсовом проекте был исследован асинхронный двигатель, получена его математическая модель, которая является адекватной. Было произведено моделирование следящего по скорости режима работы двигателя в программе Maple и получен график переходного процесса.
Литература
Справочник по электрическим машинам: В 2 т. / Под ред. И. П. Копылова и Б. К. Клокова. – М.: Энергоатомиздат, 1988.
Ключев В.И. Теория электропривода. Учебник для вузов. – М.: Энергоатомиздат, 1985.
Тихомиров В.Б. Планирование и анализ эксперимента. – М.: Легкая индустрия, 1974.
Дубовец В.С. Методические указания к выполнению курсовой работы. – Витебск: Минобразования РБ, ВГТУ, 1998.
Приложения
Приложение 1
> restart;
M_w:=[
[10, 540.83, 523.6, 509.78],
[20, 536.44, 524.05, 547.35],
[30, 554.89, 573.61, 552.02],
[40, 537.75, 560.94, 553.53],
[50, 575.04, 584.01, 590.29],
[60, 562.24, 547.81, 571.17],
[70, 566.3, 579.66, 591.48],
[80, 571.15, 594.03, 617.4],
[90, 579.05, 553.65, 541.99],
[100, 592.84, 571.99, 559.18],
[110, 563.45, 584.04, 579.38],
[120, 557.43, 535.43, 543.44],
[130, 565.68, 593.7, 600.59],
[140, 570.34, 565.22, 612.2],
[150, 586.14, 584.29, 587.06],
[160, 571.3, 547.51, 543.09],
[170, 602.04, 626.15, 656.11],
[180, 606.75, 598.77, 598.84],
[190, 562.77, 555.3, 578.28],
[200, 581.59, 554.17, 580.06],
[210, 600.61, 593.52, 574.11],
[220, 600.6, 573.35, 574.56],
[230, 599.85, 626.72, 612.46],
[240, 583.65, 555.42, 559.74],
[250, 579.57, 565.75, 551.15],
[260, 598.06, 607.93, 601.39],
[270, 571.82, 592.45, 615.3],
[280, 595.53, 581.94, 594.32],
[290, 590.68, 587.49, 614.75],
[300, 586.73, 595.49, 609.58]
]:
Ms_w:=[seq([M_w[i,1],evalf((M_w[i,2]+M_w[i,3]+M_w[i,4])/3,7)],i=1..30)];
Mtr_w:=sort(evalf(CurveFitting[LeastSquares](Ms_w,w,curve=a4*w^4+a3*w^3+a2*w^2+a1*w+a0),5));
Gr_P:=plot(Ms_w,style=point,symbol=circle,symbolsize=15,color=blue):
Gr_L:=plot(Mtr_w,w=0..300,style=line,thickness=2,color=red):
plots[display](Gr_P,Gr_L,labels=[w,M_tr]);
>
Приложение 2
> restart;with(plots):
Warning, the name changecoords has been redefined
> a := diff(omega(t), t) = (-omega(t)+w0-w0*Mc/Mп)/T[М];
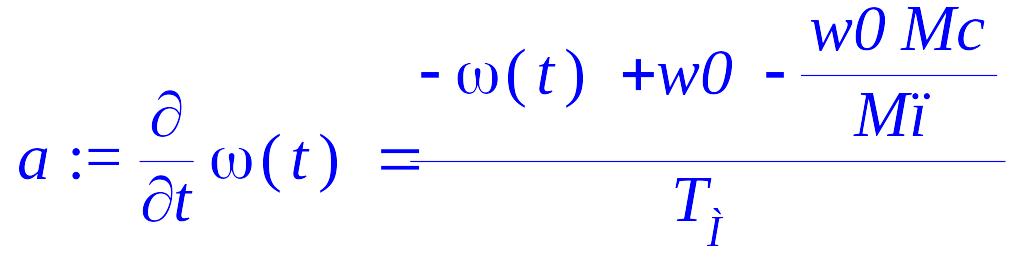
> b := dsolve({a, omega(0) = 0});
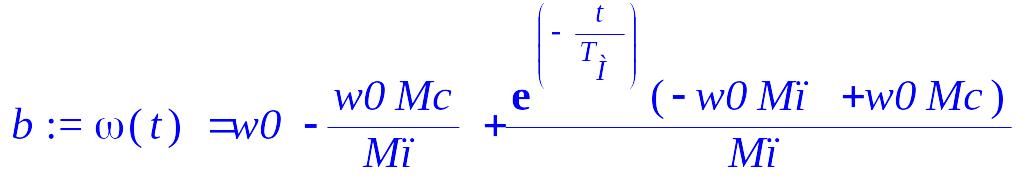
> T[М] := (Jдв+Jин+rho/w0)*w0/Mп;
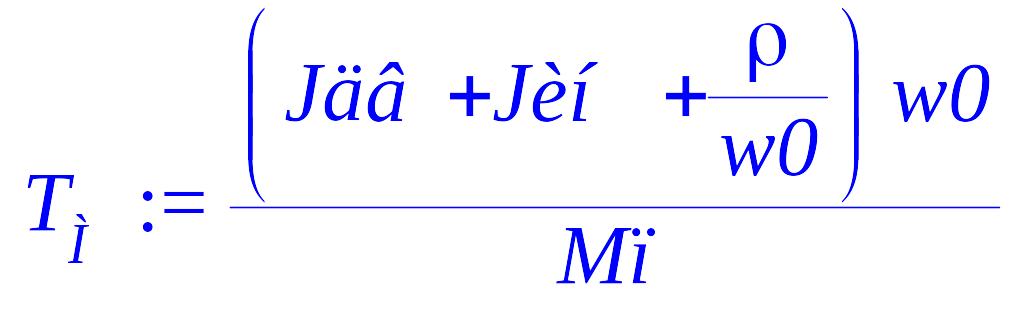
> Jдв := 2.4; Jин := 4.7; rho := .75; w0 := 314; Mc := .61; Mп := 833;
> evalf(T[М]);
> evalf(b);
> z := plot(rhs(b), t = 0 .. 8*T[М], w=0 .. 314):
> display(z);
> restart;with(plots):
Warning, the name changecoords has been redefined
> a := diff(omega(t), t) = (-omega(t)-60+w0-w0*Mc/Mп)/T[М];
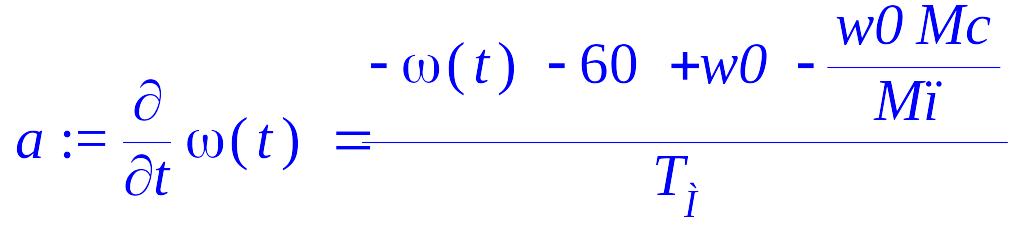
> b := dsolve({a, omega(0) = 0});
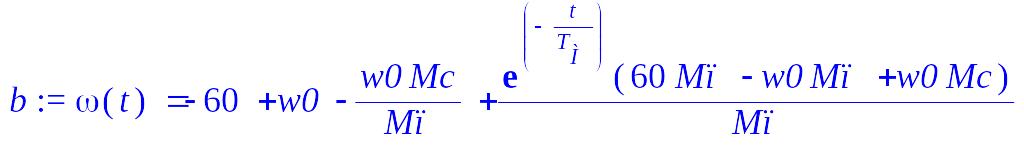
> T[М] := (Jдв+Jин+rho/w0)*w0/Mп;
> Jдв := 2.4; Jин := 4.7; rho := .75; w0 := 314; Mc := .61; Mп := 833;
> evalf(T[М]);
> evalf(b);
> z := plot(rhs(b),t = 0 .. 8*T[М], w=0 .. 314):
> display(z);
>
Подпись