2. Разработка структуры математической модели

Динамические характеристики представляют собой временные зависимости и показатели, определяющие качество работы исполнительных двигателей в переходных режимах: при пуске, торможении, реверсировании и регулировании скорости. К числу важнейших динамических показателей относится быстродействие – способность развивать заданную угловую скорость ротора с минимальным запаздыванием во времени по отношению к соответствующему изменению электрического сигнала.

Как динамическая система асинхронный трехфазный двигатель описывается нелинейным дифференциальным уравнением первого порядка:

, (2.1)

где М - электромагнитный момент, развиваемый двигателем ; М_н - статический момент сопротивления; J - момент инерции вращающихся частей – ротора и нагрузки ; J(dω/dt)=М_дин - динамический момент сопротивления.

; (2.2)

Учитывая, что ω=ω₀·(1-S), получим:

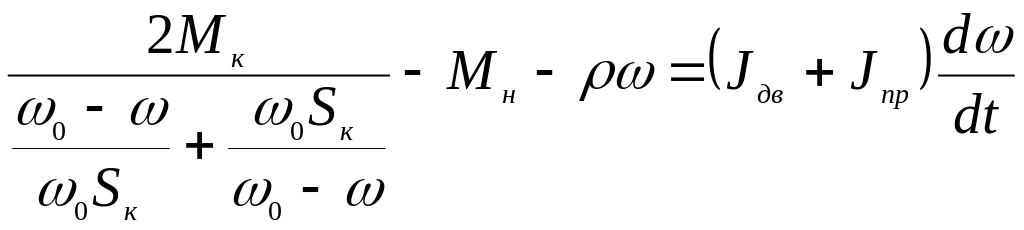(2.3)

Выражение (2.3) представляет собой математическую модель асинхронного двигателя в виде дифференциального уравнения первого порядка.

3. Разработка программы для эвм, идентификация нелинейной механической характеристики нагрузки и статистический анализ результатов

Параметры объекта можно определять как расчётным путём, так и экспериментально. Механическая характеристика нагрузки получена экспериментальным путём. Данные эксперимента приведены в виде таблицы в задании.

Рассмотрим результаты проведённого эксперимента по определению момента нагрузки в зависимости от частоты вращения привода. По заданным значениям, полученным экспериментально, находим среднее арифметическое значение момента нагрузки (Таблица 1).

Таблица 1

w, 1/c	Mн/1000, Нм			Mн ср/ 1000, Нм
10	540,83	523,60	509,78	524,74
20	536,44	524,05	547,35	535,95
30	554,89	573,61	552,02	560,17
40	537,75	560,94	553,53	550,74
50	575,04	584,01	590,29	583,11
60	562,24	547,81	571,17	560,41
70	566,30	579,66	591,48	579,15
80	571,15	594,03	617,40	594,19
90	579,05	553,65	541,99	558,23
100	592,84	571,99	559,18	574,67
110	563,45	584,04	579,38	575,62
120	557,43	535,43	543,44	545,43
130	565,68	593,70	600,59	586,66
140	570,34	565,22	612,20	582,59
150	586,14	584,29	587,06	585,83
160	571,30	547,51	543,09	553,97
170	602,04	626,15	656,11	628,10
180	66,75	598,77	598,84	421,45
190	562,77	555,30	578,28	565,45

Продолжение таблицы 1

w, 1/c	Mн/1000, Нм			Mн ср/ 1000, Нм
200	581,59	554,17	580,06	571,94
210	600,61	593,52	574,11	589,41
220	600,60	573,35	574,56	582,84
230	599,85	626,72	612,46	613,01
240	583,65	555,42	559,74	566,27
250	579,57	565,75	551,15	565,49
260	598,06	607,93	601,39	602,46
270	571,82	592,45	615,30	593,19
280	595,53	581,94	594,32	590,60
290	590,68	587,49	614,75	597,64
300	586,73	595,49	609,58	597,27

Используя усреднённое значение момента нагрузки, можно построить механическую характеристику объекта, т.е. зависимость (Рисунок 2).

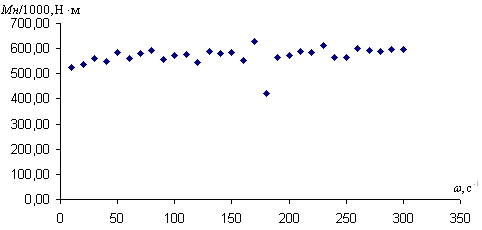
Рисунок 2 – Координаты точек эксперимента

в пространстве параметров

Анализируя полученную зависимость, можно выдвинуть гипотезу о структуре формальной статической макромодели объекта. Эту структуру можно представить в квадратичном виде:

. (3.1)

Используя программу Maple определим структуру математической модели:

> restart;

M_w:=[

[10, 540.83, 523.6, 509.78],

[20, 536.44, 524.05, 547.35],

[30, 554.89, 573.61, 552.02],

[40, 537.75, 560.94, 553.53],

[50, 575.04, 584.01, 590.29],

[60, 562.24, 547.81, 571.17],

[70, 566.3, 579.66, 591.48],

[80, 571.15, 594.03, 617.4],

[90, 579.05, 553.65, 541.99],

[100, 592.84, 571.99, 559.18],

[110, 563.45, 584.04, 579.38],

[120, 557.43, 535.43, 543.44],

[130, 565.68, 593.7, 600.59],

[140, 570.34, 565.22, 612.2],

[150, 586.14, 584.29, 587.06],

[160, 571.3, 547.51, 543.09],

[170, 602.04, 626.15, 656.11],

[180, 66.75, 598.77, 598.84],

[190, 562.77, 555.3, 578.28],

[200, 581.59, 554.17, 580.06],

[210, 600.61, 593.52, 574.11],

[220, 600.6, 573.35, 574.56],

[230, 599.85, 626.72, 612.46],

[240, 583.65, 555.42, 559.74],

[250, 579.57, 565.75, 551.15],

[260, 598.06, 607.93, 601.39],

[270, 571.82, 592.45, 615.3],

[280, 595.53, 581.94, 594.32],

[290, 590.68, 587.49, 614.75],

[300, 586.73, 595.49, 609.58]

]:

Ms_w:=[seq([M_w[i,1],evalf((M_w[i,2]+M_w[i,3]+M_w[i,4])/3,7)],i=1..30)];

Mtr_w:=sort(evalf(CurveFitting[LeastSquares](Ms_w,w,curve=a4*w^4+a3*w^3+a2*w^2+a1*w+a0),5));

Gr_P:=plot(Ms_w,style=point,symbol=circle,symbolsize=15,color=blue):

Gr_L:=plot(Mtr_w,w=0..300,style=line,thickness=2,color=red):

plots[display](Gr_P,Gr_L,labels=[w,M_tr]);

. (3.6)

Строим график по данному уравнению в программе Maple (Рисунок 3).

Рисунок 3 – Механическая характеристика нагрузки

По экспериментальным данным найдём дисперсию отклика:

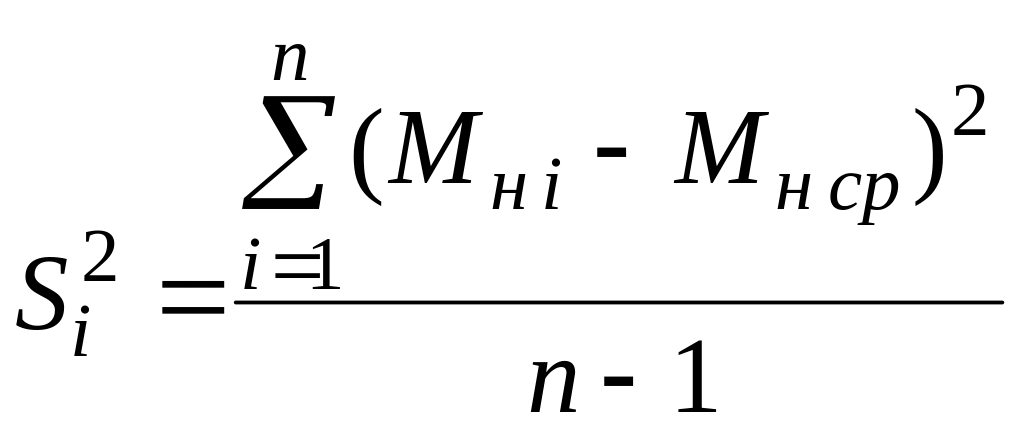, (3.7)

где п- количество повторений в каждой точке опыта (п=3).

После этого вычислим основную характеристику проведенного эксперимента – дисперсию воспроизводимости по формуле:

, (3.8)

где N – количество опытов в эксперименте (N=30).

Несмотря на достигнутое качество проведения опытов, в каждой точке эксперимента дисперсии опытов могут сильно отличаться, то есть быть неоднородными. Этот факт выявляется с помощью критерия однородности дисперсий – критерия Кохрена:

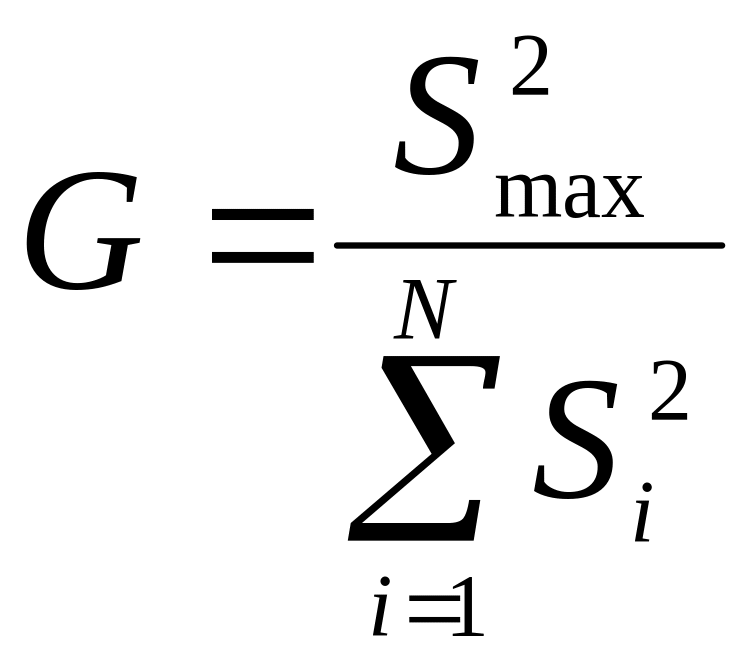, (3.9)

где - максимальное значение из всех дисперсий.

Для проверки адекватности модели найдем значения квадратов невязок в каждой точке эксперимента:

. (3.10)

Определим дисперсию адекватности:

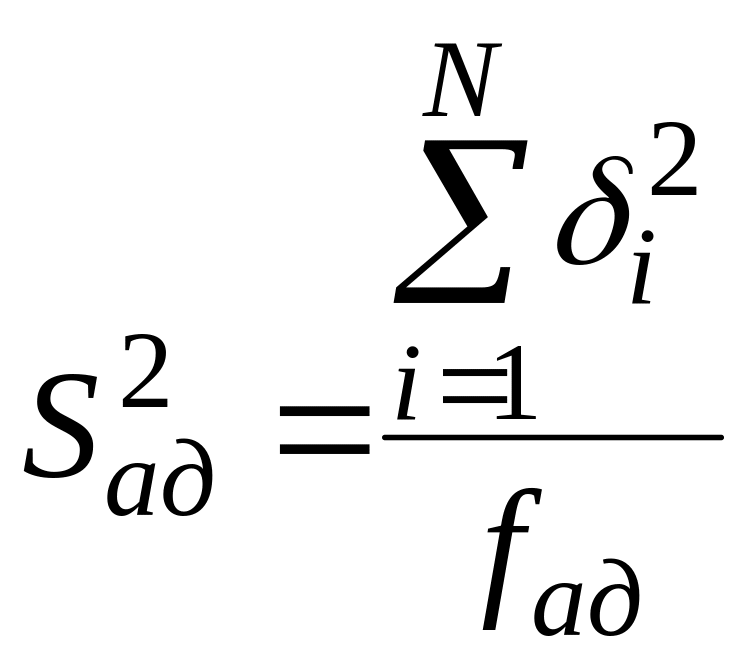, (3.11)

где - число степеней свободы, связанное с адекватностью ( , k – число коэффициентов уравнения модели (k=5)).

Найдём критерий Фишера:

. (3.12)

Все значения параметров, рассчитанные по формулам (3.7) и (3.10), приведены в таблице 2.

Таблица 2

w, 1/с	Мн, 1/1000 Нм			Mн ср, 1/1000 Нм	Дисперсия отклика	Mн', 1/1000 Нм	Квадрат невязки
10	540,83	523,6	509,78	524,7367	241,99463	5,21E+02	16,2936
20	536,44	524,05	547,35	535,9467	135,90503	5,40E+02	13,5692
30	554,89	573,61	552,02	560,1733	137,46723	5,54E+02	39,5688
40	537,75	560,94	553,53	550,7400	140,28210	5,64E+02	179,4587
50	575,04	584,01	590,29	583,1133	58,74363	5,71E+02	146,1535
60	562,24	547,81	571,17	560,4067	138,94323	5,75E+02	216,9430
70	566,3	579,66	591,48	579,1467	158,70573	5,77E+02	4,5371
80	571,15	594,03	617,4	594,1933	534,78563	5,77E+02	289,8697
90	579,05	553,65	541,99	558,2300	359,09320	5,76E+02	317,4021
100	592,84	571,99	559,18	574,6700	288,63570	5,74E+02	0,3684
110	563,45	584,04	579,38	575,6233	116,57143	5,72E+02	16,2881
120	557,43	535,43	543,44	545,4333	123,98003	5,69E+02	552,7047
130	565,68	593,7	600,59	586,6567	341,88343	5,66E+02	409,9671
140	570,34	565,22	612,2	582,5867	664,26573	5,64E+02	337,3084

150	586,14	584,29	587,06	585,8300	1,99030	5,63E+02	541,0770
160	571,3	547,51	543,09	553,9667	230,21743	5,62E+02	58,2721
170	602,04	626,15	656,11	628,1000	733,74310	5,61E+02	4446,6184
180	66,75	598,77	598,84	421,4533	94360,84223	5,62E+02	19775,0597
190	562,77	555,3	578,28	565,4500	137,40690	5,64E+02	3,4434
200	581,59	554,17	580,06	571,9400	237,41490	5,66E+02	36,0240
210	600,61	593,52	574,11	589,4133	188,21103	5,69E+02	415,3499
220	600,6	573,35	574,56	582,8367	237,01803	5,73E+02	101,5243
230	599,85	626,72	612,46	613,0100	180,72610	5,77E+02	1299,8097
240	583,65	555,42	559,74	566,2700	231,21390	5,81E+02	229,3576
250	579,57	565,75	551,15	565,4900	201,97480	5,86E+02	415,7903
260	598,06	607,93	601,39	602,4600	25,21290	5,90E+02	153,7631
270	571,82	592,45	615,3	593,1900	473,03830	5,94E+02	0,1770
280	595,53	581,94	594,32	590,5967	56,56943	5,96E+02	30,8215
290	590,68	587,49	614,75	597,6400	222,10810	5,97E+02	0,1571
300	586,73	595,49	609,58	597,2667	132,89803	5,96E+02	0,7118
				Максимальная дисперсия	Сумма дисперсии		Сумма невязок
				94360,84223	101091,84227		30048,3895

Критерий Кохрена	Дисп.воспр.	Дисп.адекв.	Критерий Фишера
0,93342	3369,72808	1112,903314	0,330265021