Раздел 1. Дифференциальное исчисление Лекция 5. Производная и дифференциал

1. Понятие производной

Рассмотрим график непрерывной функции у=f(x). Возьмем на этом графике точку М₀(x₀, у₀). Определим тангенс угла наклона касательной прямой к графику у=f(х), проведенной в точке М₀ (рис.1).

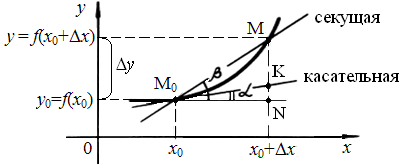
Рис. 1

Точка М₀ имеет координаты х₀, у₀=f(х₀). Дадим переменной х приращение x и переместимся по графику из точки М₀ в точку М с координатами: абсциссой х₀ + х, ординатой у₀ + y = f(х₀ + х). При перемещении из точки М₀ в точку M значение функции изменилось на величину у. Это изменение называется приращением функции и вычисляется так:

y = y – y₀ = f(x₀+x) – f(x₀).

Проведем секущую прямую М₀М. Тангенс угла наклона к оси ОХ (угловой коэффициент) секущей может быть найден из прямоугольного треугольника М₀МN как отношение противолежащего катета |MN| к прилежащему |M₀N|:

.

Когда точка М вдоль кривой будет перемещаться к точке M₀, секущая М₀М будет вращаться вокруг точки M₀ и неограниченно приближаться к некоторой прямой М₀К с углом наклона  (М₀М  М₀К). Это предельное положение секущей является касательной к графику у=f(х) в точке М₀.

В этом случае неограниченно уменьшаются приращение аргумента х (х0) и приращение функции у0 (наша функция непрерывна).

Угол  наклона секущей к положительному направлению оси OX превратится в угол наклона касательной . Тогда угловой коэффициент касательной прямой k получим так:

,

т.е. угловой коэффициент касательной есть предел отношения приращения функции у к приращению аргумента х при стремлении х к нулю.

Определение 1. Производной функции у=f(х) в точке х₀ называется предел отношения приращения функции у = f(х₀+х) – f(x₀) к приращению аргумента х при стремлении х к нулю, если такой предел существует.

.

Другие обозначения производной функции в точке х₀:

у'(х₀), .

Нахождение производной функции называется дифференцированием функции.

Если функция в точке х имеет конечную производную, то функция называется дифференцируемой в этой точке.

Функция, дифференцируемая во всех точках промежутка X, называется дифференцируемой на этом промежутке.

Определение 2. Функция f(х) имеет производную на интервале (a, b), если производная f'(х₀) существует в каждой точке х₀ этого интервала.

Учитывая это, в дальнейшем иногда будем опускать индекс «0» у величины х₀ и записывать производную так: f'(х).

Производную функции f(х) можно вычислять при различных значениях х (не только в точке х₀), т.е. величина производной зависит от значения аргумента х. Поэтому, если функция f(х) имеет производную в каждой точке множества X, то производная f'(x) также является функцией от аргумента х, определенной на множестве Х.

2. Механический, физический и экономический смысл производной

Механический смысл производной: скорость прямолинейного движения материальной точки в момент времени t₀ есть производная от пути по времени:

.

Пусть материальная точка движется по прямой в одном направлении. Обозначим S – путь, пройденный точкой, а t – время. Путь, пройденный точкой за время t, зависит от t и изменяется по некоторому закону S=S(t). Поставим задачу определить скорость материальной точки V₀ в некоторый момент времени t₀. Для этого рассмотрим другой момент времени по прошествии отрезка t, т.е. момент t₀+t. К моменту t₀ пройденный точкой путь составит S(t₀); к моменту t₀+t точка пройдет путь S(t₀+t). За промежуток времени t точка прошла путь S = S(t₀+t) – S(t₀). Средняя скорость движения за время t составит отношение . Эта средняя скорость отличается от мгновенной скорости в момент t₀, и величина V_cp тем ближе к скорости V₀, чем меньше промежуток t. Устремим t к нулю (t0). Тогда предел, к которому стремится средняя скорость, является скоростью точки V₀ в момент t₀:

Здесь рассматривается предел отношения приращения пути S к приращению времени t.

Физический смысл производной: Обобщая предыдущий закон V = S'(t), можно сказать, что если функция у = f(t) описывает физический процесс, меняющийся со временем t, то производная у' = f'(t₀) есть скорость протекания этого процесса в момент t₀.

Экономический смысл производной.

Производительность труда в момент t₀ – предельное значение средней производительности за период времени от t₀ до t₀ + Δt при Δt  0, т. е.

Здесь ΔQ – количество произведенной продукции за интервал времени Δt. Производительность труда u – скорость роста объема продукции Q.

Предельный продукт. Пусть функция Q(x) – зависимость количества произведенной продукции от величины затрат ресурса х. Отношение – средняя величина продукта, соответствующая величине затрат в размере Δх. Предельный (маржинальный) продукт при затратах ресурса х₀: