Основные свойства функций
1. Четность и нечетность.
Функция у=f(х) называется четной, если для всех х из области определения выполняется f(-х)=f(х), и нечетной, если f(-х)=-f(х). В противном случае функция у=f(х) называется функцией общего вида.
График четной функции симметричен относительно оси ординат (рис.1).
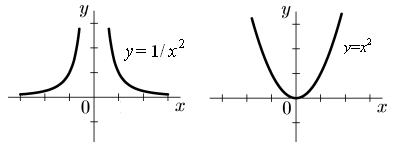
Рис. 1.Четные функции
Примеры четных функций: y=1/x2; y=x2; y=cos x; y=|x|.
График нечетной функции симметричен относительно начала координат (рис.2).
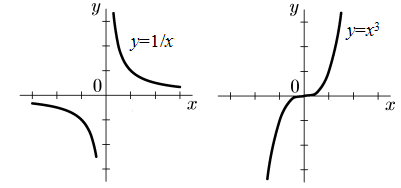
Рис.2. Нечетные функции
Примеры нечетных функций: y=1/x; у=х3; у=х; y=tg x.
Функция общего вида не является ни четной, ни нечетной.
Её график не симметричен ни относительно оси ординат, ни относительно начала координат (рис.3).
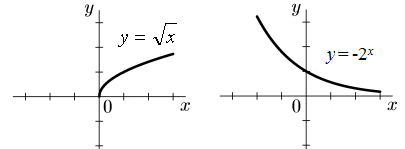
Рис.3. Функции общего вида
Примеры функций
общего вида:
;
y=-2x;
.
2. Монотонность.
Функция у = f(х) называется возрастающей (убывающей) на интервале (а,b), если большему значению аргумента х в этом интервале соответствует большее (меньшее) значение функции.
Это значит, что для любых значений х1 и х2 из интервала (а,b) неравенству х1<х2 в случае возрастания функции соответствует неравенство f(x1) < f(x2), а в случае убывания – неравенство f(x1) > f(x2) (рис. 4).
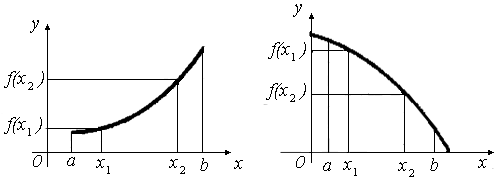
Рис.4 (a). Возрастающая функция Рис.4 (б). Убывающая функция
Функции возрастающие и убывающие называются строго монотонными.
К монотонным функциям относятся неубывающие и невозрастающие функции, т.е. такие, для которых при х1<х2 выполняются, соответственно, неравенства f(x1) ≤ f(x2) и f(x1) ≥ f(x2).
Например, функция y=x2 при xє(-∞;0] убывает, при xє[0;+∞) возрастает.
3. Ограниченность.
Функция у=f(x) называется ограниченной на интервале (а, b), если существует такое положительное число M > 0, что для всех х из данного интервала выполняется неравенство |f(x)| М.
Например, тригонометрические функции y=sin x и y=cos x ограничены на всей числовой оси (-∞;+∞) и число М для них равно 1, так как |sin x| 1 и |cosx|1.
График ограниченной функции лежит в полосе -М у М (рис.5).
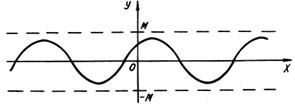
Рис.5. Ограниченная функция
4. Периодичность.
Функция у=f(х) называется периодической с периодом Т, если для любых x из области определения функции выполняется f(хТ) = f(х).
Период – наименьшее из положительных чисел, удовлетворяющих данному свойству.
Примерами периодических функций служат тригонометрические функции y=sinx, у=соsx, у=tgx, y=ctgx. Период первых двух функций равен 2 (так как для любых xєR sin(x+2)=sinx и соs(x+2)=соsx, а две последние имеют период, равный : tg(x+)=tgx и ctg(x+2)=ctgx.
График периодической функции достаточно построить на отрезке длины Т, далее эта кривая повторяется на всю область существования функции (рис.6).
Рис.6. Периодическая функция
Основные элементарные функции
К основным элементарным функциям относятся функции:
1) Степенная функция:
,
где n
– действительное число (nєR).
2) Показательная
функция:
,
где а
– положительное число, не равное единице
(a >
0, а≠1).
3) Логарифмическая
функция:
,
где
– положительное число, не равное единице
(a >
0, а≠1).
4) Тригонометрические
функции:
,
,
,
.
5) Обратные тригонометрические функции:
,
,
,
.
Свойства и графики основных элементарных функций
1) Степенная функция .
1. n=0, y = x0.
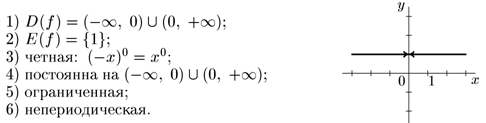
2. n=1, y = x
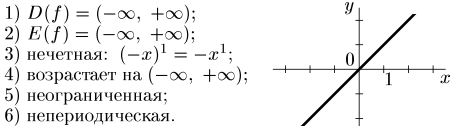
3. y = xn, nєN
n – нечетное натуральное число ≥ 3.
4. y = xn, nєN
n – четное натуральное число .
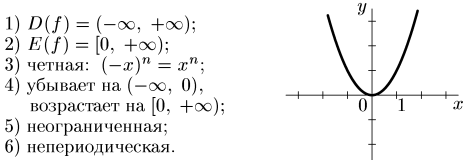
5. y = x –n, nєN
n – нечетное натуральное число.
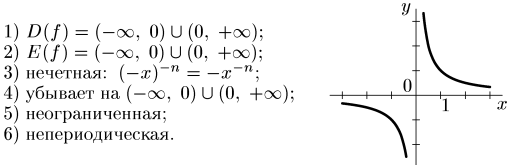
6. y = x –n, nєN
n – четное натуральное число.
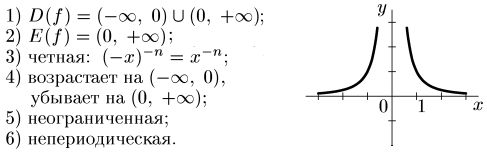
7.
,
nєN
n – нечетное натуральное число, n>1.
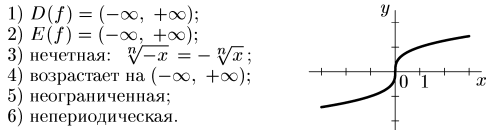
8. , nєN
n – четное натуральное число.
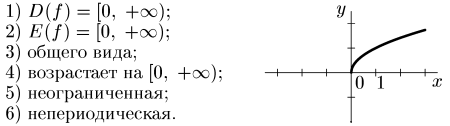
2) Показательная функция
1. ; 0 < а < 1, а≠1.
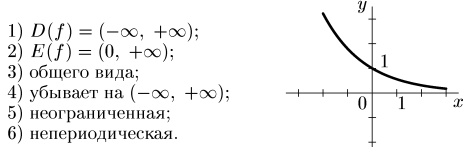
2. ; a > 1, а≠1.
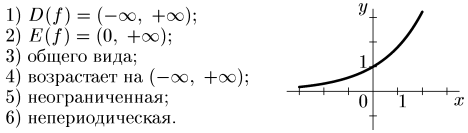
3) Логарифмическая
функция
.
1.
;
0 < а
< 1, а≠1.
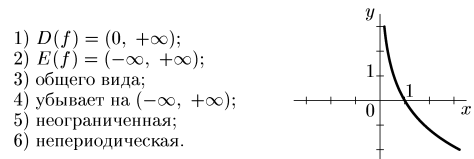
2. ; а > 1, а≠1.
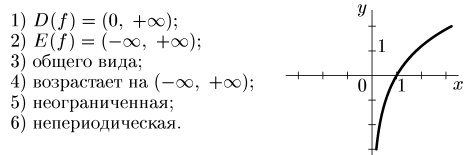
4) Тригонометрические функции
1. y = sin x
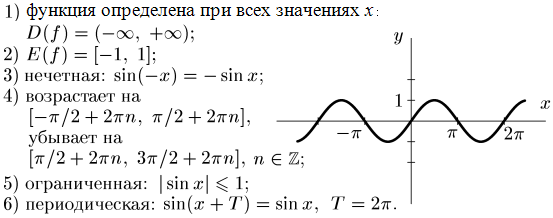
2. у = соs x
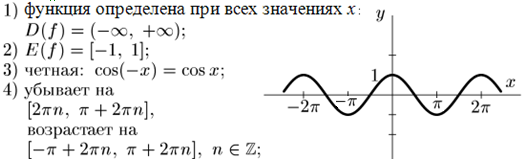
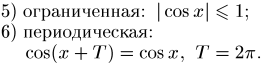
3. у = tg x
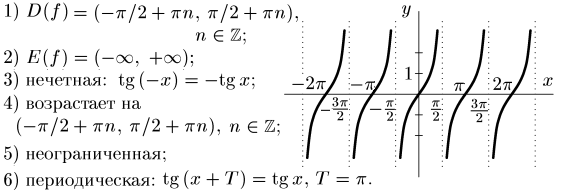
4. у = ctg х
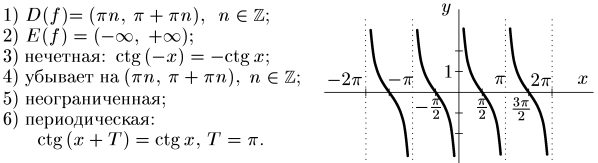
5) Обратные тригонометрические функции
1. y = arcsin x
2. у = arcсоs x
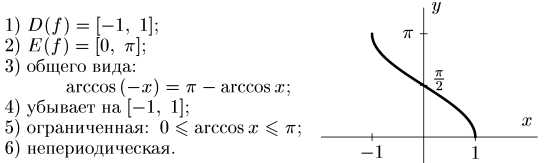
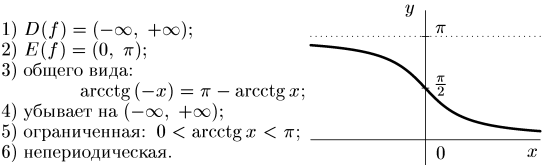
3. у = arctg x
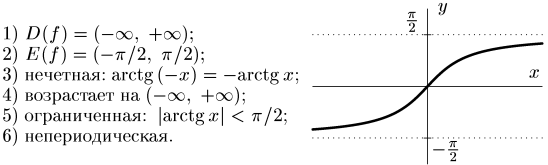
4. у = arcctg x
