Раздел 1. Дифференциальное исчисление Лекция 1. Функция

1. Множества и операции над ними

Множество – совокупность объединенных по некоторому признаку объектов. Объекты, образующие множество, называются его элементами или точками.

Запись aєA означает, что элемент а принадлежит множеству A. Запись b A означает, что элесент b не принадлежит множеству A.

Обычно множества обозначают большими буквами латинского алфавита A, B, С, ..., X, У, Z, ..., а их элементы – малыми буквами латинского алфавита: а, b, с, ..., х, у, z, ... .

Иногда множество записывают с помощью фигурных скобок: А = {а₁; а₂; а₃; ...; а_п}.

Пустое множество – которое не содержит ни одного элемента; обозначается символом Ø.

Бесконечное множество – которое содержит любое конечное число элементов.

Множество В называется подмножеством (частью) множества A, если каждый элемент множества В является элементом множества A. Символически это обозначают так: В A.

Два множества А и В называются равными, если они состоят из одних и тех же элементов: А = В.

Числовые множества – множества, элементами которых являются числа.

Объединением двух множеств А и В называется множество С, состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств:

С = A В = {х | х є А или х є В}.

Пересечением двух множеств А и В является множество С, состоящее из элементов, которые принадлежат каждому из множеств А и В:

С = A В = {х | х є А и х є В}.

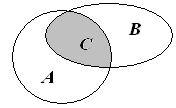
Разностью множеств А и В называется множество С, состоящее из всех элементов множества А, которые не принадлежат множеству В:

С = A \ В = {х | х є А, х В}.

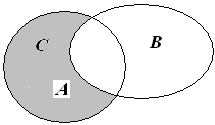
Если В A (В – подмножество множества A), то разность С = A \ В называется дополнением множества В до множества A.

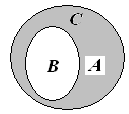
Пример. Объединение: {1; 5; 6; 7} {2; 5; 6; 9} = {1; 2; 5; 6; 7; 9};

Пересечение: {1; 5; 6; 7} {2; 5; 6; 9} = {5; 6};

Разность: {1; 5; 6; 7} \ {2; 5; 6; 9} = {1; 7}.

Прямое (декартовое) произведение множеств A и В – это множество C=AхВ, элементами которого являются все упорядоченные пары (x, y), в которых х є А, y є В.

A={2; 3; 9}; B={1; 4}. C=AхВ={(2; 1); (2; 4); (3; 1); (3; 4); (9; 1); (9; 4)}.

2. Вещественное (действительное) число и числовая прямая

Понятие действительного числа вводится поэтапно.

Вначале возникло множество натуральных чисел – для нумерации или для счета: N = {1, 2, 3, ...}.

Если к множеству N добавить 0 и отрицательные целые числа, то получится множество целых чисел Z = {…, -3, -2, -1, 0, 1, 2, 3, ...}, т.е. N Z.

Целые и дробные числа составляют множество рациональных чисел Q, которые выражаются отношением двух целых чисел: и т.д.

Всякое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби:

– чистая бесконечная периодическая дробь (период равен 3 и находится сразу после запятой),

= - 2,5(0) – смешанная конечная периодическая дробь (период равен 0);

=0,4545…=0,(45);

0,2(5) – смешанная бесконечная периодическая дробь.

По бесконечной периодической дроби можно найти рациональное число в виде обыкновенной дроби.

Пример 1. Найти рациональное число, равное смешанной бесконечной периодической дроби 0,43(1998).

Решение. Искомое рациональное число обзначим через x:

x = 0,43(1998) = . В знаменателе степень 2 – число цифр до периода, степень 4 – число цифр в периоде.

Пример 2. Найти рациональное число, равное 1,2(3).

Решение. x = 1,2(3) = .

Пример 3. Найти рациональное число, равное 0,12(34).

Решение. x = 0,12(34) = .

Иррациональные числа I выражаются бесконечной непериодической десятичной дробью. Например, , , π=3,141592654… и т.д.

Множества рациональных и иррациональных чисел составляют множество действительных чисел R = Q I.

Между множествами N, Z, Q и R существует соотношение N Z Q R.

Геометрически множество R изображается точками числовой прямой (или числовой оси) – прямой, на которой выбрано начало отсчета, положительное направление и единица масштаба.

Между множеством действительных чисел R и точками числовой прямой существует взаимно однозначное соответствие, т. е. каждому действительному числу соответствует определенная точка числовой прямой, и наоборот, каждой точке прямой – определенное действительное число. Поэтому часто вместо «число х» говорят «точка х».

Множество действительных чисел R дополняют двумя элементами, обозначаемыми -∞ и +∞ и называемыми «минус бесконечность» и «плюс бесконечность» (или бесконечно удаленными точками).

Множество R, дополненное элементами -∞ и +∞, называется расширенным множеством действительных чисел (расширенной числовой прямой) и обозначается .

Для бесконечно удаленных точек справедливы правила:

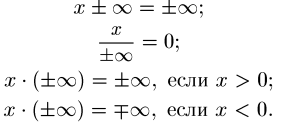
Порядок чисел на естественный: всякое действительное число меньше +∞ и больше -∞, т.е. если х є R, то -∞ < х < +∞.

-∞ на числовой прямой находится левее всех чисел, +∞ – правее всех чисел.

Иногда R дополняют одним элементом ∞, называемым бесконечностью или бесконечно удаленной точкой.

Возьмем на числовой прямой две точки: а и b. Тогда множество, элементы которого удовлетворяют:

- неравенству а ≤ х ≤ b, называется отрезком [а; b];

- неравенству а < х < b – интервалом (а; b);

- неравенствам а ≤ х < b или а < х ≤ b – полуинтервалами соответственно [а; b) и (а; b].

Наряду с этим рассматриваются бесконечные интервалы и полуинтервалы (-∞; b), (а; +∞), (-∞,+∞), (-∞; b], [a; +∞).

Все указанные множества объединяют термином промежуток X.

Если представить, что некоторая точка х на числовой прямой движется вправо к бесконечно удаленной точке, то записывают х+∞ (x стремится к плюс бесконечности), если влево, то х -∞ (x стремится к минус бесконечности).