Исследование модели сбалансированного роста с альтернативными ресурсами.

Уравнения (2.29) решаются итеративным методом Ньютона. Для этого они должны быть приведены к линейному виду. Пусть для равенств (2.6) выполняются соотношения (2.12), (2.14). Разобьем вектор на подвекторы , где и . Разобьем, далее, вектор на подвекторы и . Тогда при экзогенно заданных и равенства (2.6) могут рассматриваться как уравнения относительно , , ,

, (2.31)

где

В дальнейшем для выделения экзогенных параметров опустим знак «’» у всех , , , полагая их переменными. Функции , всюду непрерывны вместе с первыми производными.

Е сли - некоторое начальное приближение к решению с нужной точностью, можно построить итерационный процесс, который на -ом шаге приобретает вид:

, (2.32)

Если вместо системы (2.31) воспользоваться эквивалентной ей системой (2.27), итерационный процесс на -ом шаге может быть записан в виде:

, (2.33)

Если в (2.33) принять , то на первом шаге итерации получаем:

, (2.34)

Уравнения (2.34) представляют собой линеаризованную форму уравнений (2.29).

Теорема 1. Для существования единственного решения системы (2.32) необходимо, чтобы:

1. в пределах любых строк соответствующей ей системы (1.9) производилось в сумме не более замен и эндогенных приращений вектора ;

2. выполнялось по крайней мере одно из условий:

a)

б)

где , - подмножества коэффициентов , в - м и - м столбцах.

Доказательство. Поскольку в (2.34) число уравнений равно числу неизвестных, условия теоремы выполняются лишь в случае, когда , где - главная матрица системы (2.34).

Матрицу представим состоящей из трех матриц:

, (2.35)

где , ,

Представим главный определитель системы (2.34) в виде:

, (2.36)

где - один из миноров порядка определителя , образованный из вычеркиваем каких-либо строк; - алгебраическое дополнение минора в .

Пусть при этом количества строк (1.9), не охваченных заменами и не содержащих эндогенных компонент вектора , больше, чем .

Из (2.35) следует, что в этом случае число нулевых строк в также больше . Тогда каждый из миноров в разложении (2.36) содержит нулевую строку, и .

Если же количество строк(1.9), не охваченных заменами и не содержащих эндогенных компонент вектора , не более , то (2.36) может содержать ненулевые слагаемые, тогда , что доказывает условие 1) теоремы.

Выполнение условий , , означает равенство соответствующих столбцов определителя ; при этом .

Нарушение же данных условий означает возможность соблюдения неравенства , что доказывает условие 2) теоремы.

Теорема 1 накладывает структурные ограничения на распределение эндогенных параметров (замен и конечных выпусков) в балансовой системе.

Рассмотрим примеры различной конфигурации эндогенных параметров.

Пример 2.1. ; экзогенные параметры: , , , , , , ; эндогенные параметры: , , , , ;

Решение:

Элементы главного определителя системы (2.32):

Тогда

Условия теоремы 1 не выполняются, единственного решения системы (2.32) не существует.

Пример 2.2. ; экзогенные параметры: , , , , , , ; эндогенные параметры: , , ;

Решение:

Определяя элементы главного определителя аналогично Примеру, получаем:

В этом случае выполняется условие 1) теоремы 1.

Если , выполняется условие 2) и тогда система (2.32) имеет единственное решение.

Более сложные варианты схематически изображены на рис. 2.1, 2.2. Отраслям балансовой системы соответствуют пронумерованные горизонтальные и вертикальные линии. Стрелки соединяют -ю и -ю строки в каждой замене. Отрасли с эндогенными приращениями конечного выпуска отмечены черными квадратами в правой части схемы. На рис. 2.2, кроме того эти отрасли соединены дужками с -ми отраслями. Расположение соответствующего коэффициента также отмечено черным квадратом.

На рис. 2.1:

а) структурные ограничения нарушаются, так как пять экзогенных параметров находятся в четырех строках: второй, третей, четвертой и шестой;

б) в случае структурные ограничения нарушаются, так как не выполняется условие 2) теоремы.

В двух остальных случаях условия теоремы выполняются, структурные ограничения соблюдаются.

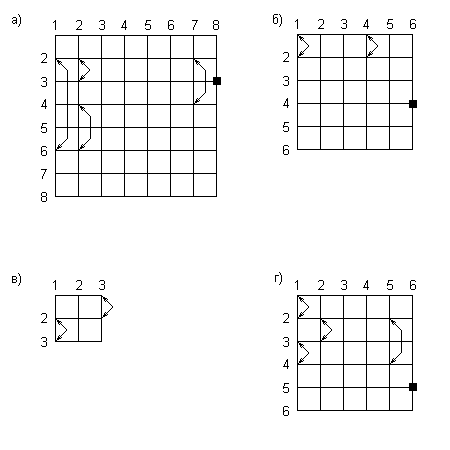
Рис. 2.1. Случай простых замен.

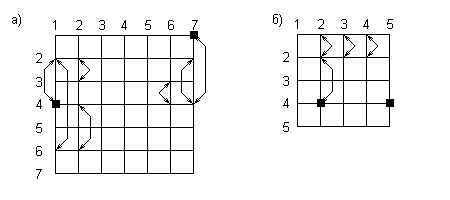
Рис. 2.2. Случай сложных замен.

На рис. 2.2:

а) условия теоремы выполняются.

б) условия теоремы нарушаются.

Если конфигурация возможных (технологически допустимых) замен и назначенных номеров эндогенных приращений конечного выпуска не удовлетворяет условиям теоремы 1, в уравнениях (1.9) следует оставлять лишь структурно допустимые. Прочие сдвиги производятся уже для системы (2.6). С точки зрения конечного результата последовательность выбираемых эндогенных параметров не имеет значения. Он определяется итоговой матрицей коэффициентов затрат.

В пределах -го шага итерационного процесса структурные ограничения определяют область аддитивных реакций балансовой системы на экзогенные изменения параметров.

Исследуем сходимость метода Ньютона для решений уравнений межотраслевого баланса переменной структуры. Используем для этой цели модель в форме (2.31).

Если решение системы (2.31) существует, в точке матрица (2.35) не вырождена, то существует такая окрестность , что при любых последовательность сходится к решению .

Обозначим:

,

,

Введем в рассмотрение матрицу , в которой:

,

где ,

;

где

;

;

,

где ; ;

Для любых в силу теоремы Ньютона получим:

, (2.37)

Определим матрицу , обозначив .

Обозначим через и число замен соответственно в -ых и -ых столбцах (2.29); . Тогда , и (2.37) может быть представлено в виде:

, (2.38)

Опустим пока индекс , подразумевая дальнейшие выкладки справедливыми для каждого шага. Тогда:

, (2.39)

где

Для (2.38),(2.39) отметим, что при и возможности роста определяются состоянием отрасли ресурсов; если и , получаем задачу стабилизации.

Проиллюстрируем процесс решения уравнений межотраслевого баланса переменной структуры (МБПС) на частном примере.

Пример 2.3. Для уравнения (1.9) заданно: , ;

экзогенные параметры: , , , ; эндогенные параметры: , , .

; .

Для первого цикла:

Лемма 1. Последовательность в итерационном процессе (2.26) при выполнении условий теоремы 1 сходятся к решению системы (2.25) не более, чем за два шага, область сходимости неограниченна.