2. Пусть в системе статического мб (5/5) затраты I-ro и t-ro продуктов на изготовления j- го продукта взаимозаменяемы с коэффициентом заменяемости

, - приращение соответствующих коэффициентов прямых затрат, вызванных заменами;

М - множество технологически допустимых замен.

Введением соотношения (7.1) мы отказываемся от предложения о независимости технологических коэффициентов. Соотношение (7.1) описывает наиболее простую форму заменяемости, когда отрасль отождествляется с одним продуктом, а замена не вызывает дополнительных изменений коэффициентов в j-м столбце. В результате замен получаем новые значения коэффициентов прямых затрат, связанных заменами:

Прочие коэффициенты остаются прежними.

Новую матрицу коэффициентов прямых затрат обозначим через А’. Тогда:

Где , - новые значения векторов валового и конечного выпусков.

Задача формулируется следующим образом. Для системы (5.5) задано множество М замен, связанных соотношениями (7.1). Требуется установить такую зависимость между приращением в каждой замене и приращением , при которой Y = Y’. Приращение второго коэффициента определиться затем из (7.1).

Воспользуемся приближенным уравнением:

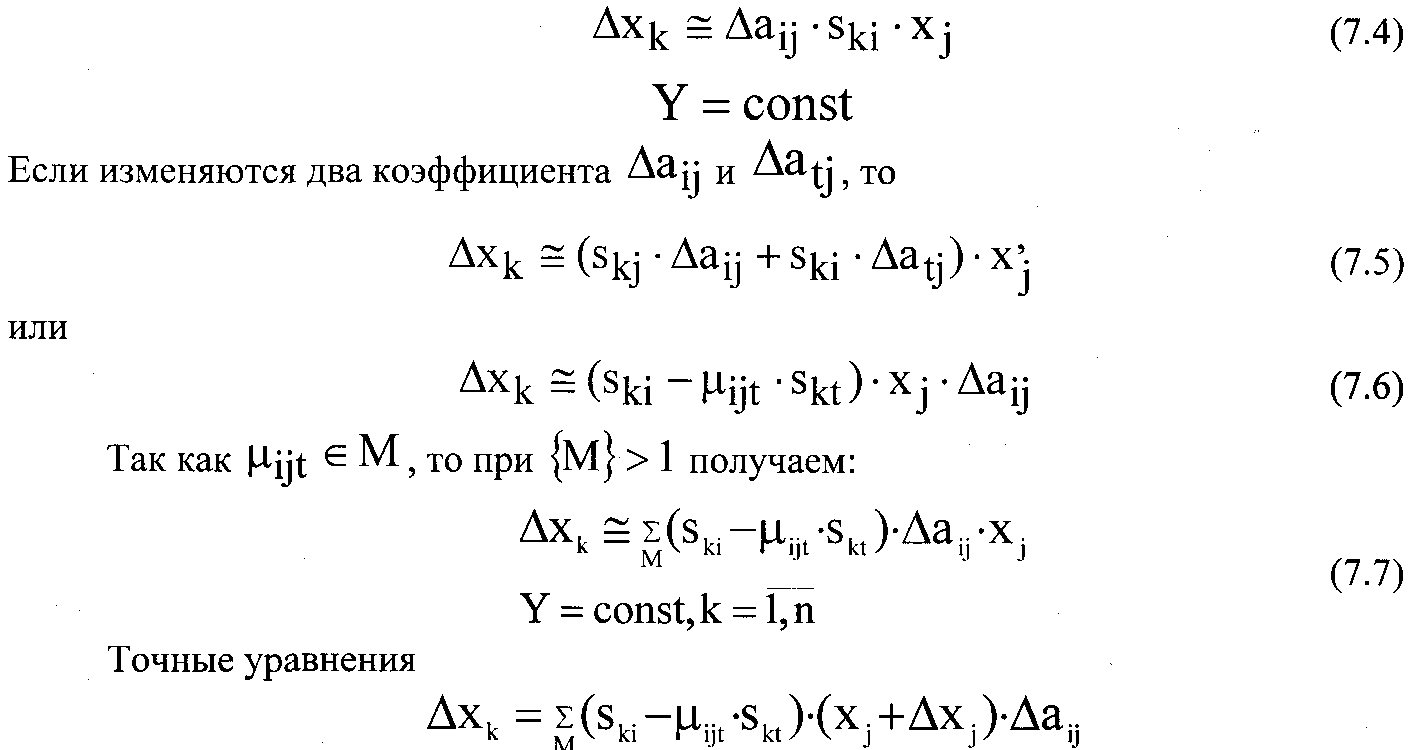
Они образуются из системы:

с учётом соотношений (7.1).

Полагая в (7.7) неизвестными n любых элементов из совокупности всех и и экзогенно задавая остальные, получим систему из n уравнений с n неизвестными. Пусть, например, неизвестны все 1 приращений и n-1 компонент вектора . Заданные 1 компонент вектора обозначим через р,

неизвестные компоненты – через . Тогда при соответствующей нумерации строк получим:

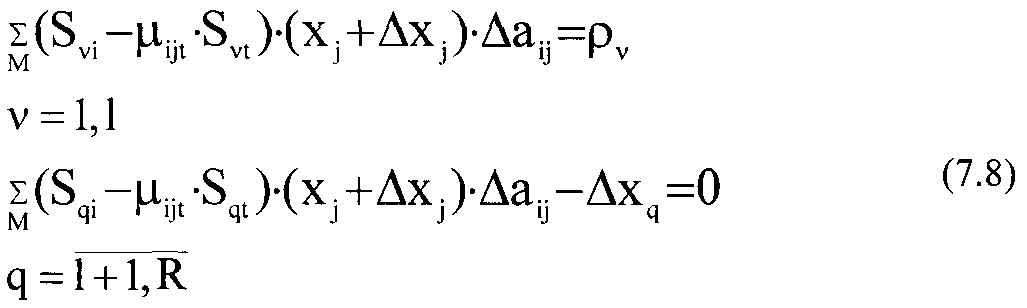
В последней системе (7.8) приближенные неравенства заменены на строгие.

Лекция № 13. МОДЕЛИ МБПС, ОРИЕНТИРОВАННЫЕ НА СТАБИЛЬНЫЙ СПРОС

1. Типы ограничений, накладываемых на модели стабилизации.

2. Основные свойства и область использования моделей стабилизации.

1. Система (7.8) представляет собой нелинейные уравнения, которые решаются итеративным методом Ньютона.

Теорема. Для существования решения системы (7.8) необходимо, чтобы в пределах любых l строк соответствующей ей системы (5.5) производилось не более l замен.

Условие теоремы накладывает структурные ограничения на распределение пар i и t, связанных заменами между отраслями. Другая группа ограничений носит количественный характер. Решение системы (7.8) имеет экономический смысл лишь при А’> 0, X’> 0. Следовательно:

(7.9)

2. Решения уравнений (7.8) без количественных ограничений (7.9) позволяют оценить всю сумму межотраслевых последствий использования заменителей, в первую очередь предметов труда, анализ решений реальных межотраслевых балансов показал, что в широком диапазоне изменений коэффициентов заменяемости наблюдаются разные по знаку изменения отраслевых валовых объемов. Лишь наиболее эффективные заменители дают экономию одновременно во всех отраслях. В настоящее время этот метод наиболее эффективен при оценке системных последствий использования новшеств. Оказалось, что так называемые "прогрессивные" материалы оказываются прежде всего инструментом межотраслевого маневрирования, а не непосредственной экономии живого труда.

Для того, чтобы правильно определить масштабы направленных структурных сдвигов, необходимо дозировать уровень использования заменителя. В этом случае необходимо учитывать ограничения (7.9), но это требует применения более сложных методов нелинейного программирования.

Лекция № 14. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ЭКОНОМИЧЕСКОГО РОСТА

1. Проблемы качества экономического роста.

2. Модели инновационного роста на основе МБПС.

3. Исследование свойств модели роста.

2.2 Матричные модели роста с альтернативными ресурсами.

Неоднозначность удельных затрат ресурсов меняет пропорции производства в процессе развития предприятия.

Исследуем возникающие при этом закономерности сбалансированного роста. По–прежнему будем пренебрегать сопутствующими заменам временными лагами.

Пусть в равенствах (1.9) известны величины , , , соответственно в (1.15) , , . Известно также множество замен , , связанных соотношениями (2.12), (2.14). Положим в (2.6) , , , .

Условие . (или, как исключение, ) означает наличие экономического роста выпуска предприятием конечной продукции, частично или полно удовлетворяющего рост внешней потребности. Тогда, как показано в [51, стр.19 ]

(2.27)

где , S=

Условие (2.27) с учетом (2.12), (2.14) примет вид:

, (2.28)

Общее число изменяемых параметров в (2.28) равно

Ограничимся случаем Полагая в (2.28) неизвестными любых элементов из совокупности всех (эндогенные параметры), и экзогенно задавая остальные, получим систему из уравнений с неизвестными.

Пусть, например, неизвестны все вариаций (приращений) и компонент векторов , . Тогда число экзогенно задаваемых компонент векторов , составит Меняя по собственному выбору ном2.2 Матричные модели роста с альтернативными ресурсами.

Неоднозначность удельных затрат ресурсов меняет пропорции производства в процессе развития предприятия.

Исследуем возникающие при этом закономерности сбалансированного роста. По–прежнему будем пренебрегать сопутствующими заменам временными лагами.

Пусть в равенствах (1.9) известны величины , , , соответственно в (1.15) , , . Известно также множество замен , , связанных соотношениями (2.12), (2.14). Положим в (2.6) , , , .

Условие . (или, как исключение, ) означает наличие экономического роста выпуска предприятием конечной продукции, частично или полно удовлетворяющего рост внешней потребности. Тогда, как показано в [51, стр.19 ]

(2.27)

где , S=

Условие (2.27) с учетом (2.12), (2.14) примет вид:

, (2.28)

Общее число изменяемых параметров в (2.28) равно

Ограничимся случаем Полагая в (2.28) неизвестными любых элементов из совокупности всех (эндогенные параметры), и экзогенно задавая остальные, получим систему из уравнений с неизвестными.

Пусть, например, неизвестны все вариаций (приращений) и компонент векторов , . Тогда число экзогенно задаваемых компонент векторов , составит Меняя по собственному выбору ном номера экзогенно задаваемых компонент, получаем необходимые, по крайней мере, условия для формирования ряда вариантов экономических постановок задач развития. Среди них отметим следующие:

1. Экзогенно задаются все и . Гибкость балансовой системы, определяемая числом технологически допускаемых альтернатив, обеспечивает необходимую структуру роста независимо от структуры отраслевых ресурсов в виде объемов валовых выпусков,

2. Необходимая структура роста обеспечивается экзогенным заданием компонент вектора . Прочие компонент вектора - эндогенные.

3. Вектор задается экзогенно. Необходимая (экзогенно задаваемая) структура роста реализуется лишь в отраслях. В прочих отраслях возможности и качество роста определяются свойствами решения уравнений (2.28), то есть эндогенно.

4. , . Экзогенно задаются компоненты вектора в любых отраслях. Прочие компоненты вектора определяются эндогенно, решением уравнения (2.28). Как видно, развитие в данном случае предусматривает стабилизацию выпуска конечного продукта и выбор вариантов его ресурсного обеспечения.

Первые три пункта из перечисленных представляют собой развитие постановок плановых задач на основе статической межотраслевой модели (см. п. 1.3) Постановка, предложенная в п.4. может быть рекомендована при разработке стратегии фирмы в условиях стабильного спроса. Свойства модели (2.28) для этого случая исследованы достаточно подробно (см. напр. 51).

Ниже исследуются свойства модели (2.28) позволяющие реализовать стратегию роста. Примем такую нумерацию строк (2.28), при которой их последовательность с меньшими значениями соответствует экзогенным параметрам . Строки для которых приращения определяются эндогенно, образуют подмножество с числом элементов . Приращения определяются эндогенно. Равенства (2.28) при этом преобразуются в уравнения:

, (2.29)

Уравнения (2.29) представляют собой наиболее общую форму модели роста, построенной на базе статической межотраслевой модели, из которой следуют перечисленные выше частные постановки.

Приращения коэффициентов прямых затрат и валовых объемов в (2.29) ограничены:

, (2.30)

где , , , , и - максимальные и минимальные величины приращений (вариаций) валовых объемов и коэффициентов прямых затрат.

Величины и задаются исходя соответственно из отраслевых ограничений по мощности и из условия неотрицательности значений валовых объемов. Они определяются, таким образом, сложившейся балансовой ситуацией. Ограничения, налагаемые на приращения коэффициентов прямых затрат , носят технологический характер и определяются масштабами допускаемых замен. В любом случае:

.

Объединенная система неравенств (2.29)-(2.30) определяет свободу выбора искомых приращений. Поскольку эта система в общем случае является нелинейной, необходимо исследовать существование и свойства её решений. Исследуем, прежде всего, условия существования и свойства решения ура уравнений (2.29), пренебрегая ограничениями (2.30).