МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ

"ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ лабораторных работ

ПО ДИСЦИПЛИНЕ

"ВЫСШАЯ ГЕОДЕЗИЯ И ОСНОВЫ ФОТОГРАММЕТРИИ"

Часть 3. "Уравнивание сети триангуляции параметрическим способом"

Донецк – ДонНТУ – 2009

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ГОСУДАРСТВЕННОЕ ВЫСШЕЕ УЧЕБНОЕ ЗАВЕДЕНИЕ

"ДОНЕЦКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ"

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ лабораторных работ

ПО ДИСЦИПЛИНЕ

"ВЫСШАЯ ГЕОДЕЗИЯ И ОСНОВЫ ФОТОГРАММЕТРИИ"

Часть 3. "Уравнивание сети триангуляции параметрическим способом"

Рассмотрено:

на заседании кафедры

маркшейдерского дела

протокол № 2

от 15.10.2009 г.

Утверждено:

на заседании учебно-

издательского совета

ДонНТУ

протокол № __

от ___.___.2009 г.

Донецк – ДонНТУ – 2009

УДК 622.1: 528

Методические указания к выполнению лабораторных работ по дисциплине "Высшая геодезия и основы фотограмметрии". Часть 3. "Уравнивание сети триангуляции параметрическим способом". // В.В. Мирный, И.В. Филатова. Донецк: ДонНТУ, 2009

Методические указания предназначены для подготовки магистров, специалистов, бакалавров, которые обучаются по формам обучения: дневная, заочная, экстернат.

Методические указания к лабораторным работам по дисциплине "Высшая геодезия и основы фотограмметрии" рекомендованы к изданию методической комиссией специальности "Маркшейдерское дело" (протокол № 2 от 15.10.2009 г.)

Авторы:

В.В. Мирный, проф.

И.В. Филатова, доц.

Рецензент:

С.Б. Кулибаба, вед. науч. сотр.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

К ВЫПОЛНЕНИЮ лабораторных работ

ПО ДИСЦИПЛИНЕ "ВЫСШАЯ ГЕОДЕЗИЯ И

ОСНОВЫ ФОТОГРАММЕТРИИ"

Часть 3. "Уравнивание сети триангуляции параметрическим способом"

Составители:

Вячеслав Васильевич Мирный

Ирина Викторовна Филатова

Уравнивание сети триангуляции параметрическим способом

Необходимо уравнять сеть триангуляции, которая состоит из 6 пунктов, из которых пункты Бург, Вассертурм, Вильмер – жесткие, а пункты Шанце, Эгидиус и Штейерндиб – определяемые.

Число нормальных уравнений, соответствующих данной сети, равно 22.

1. По материалам предварительной обработки составлена схема сети, которая приведена на рис. 3.1.

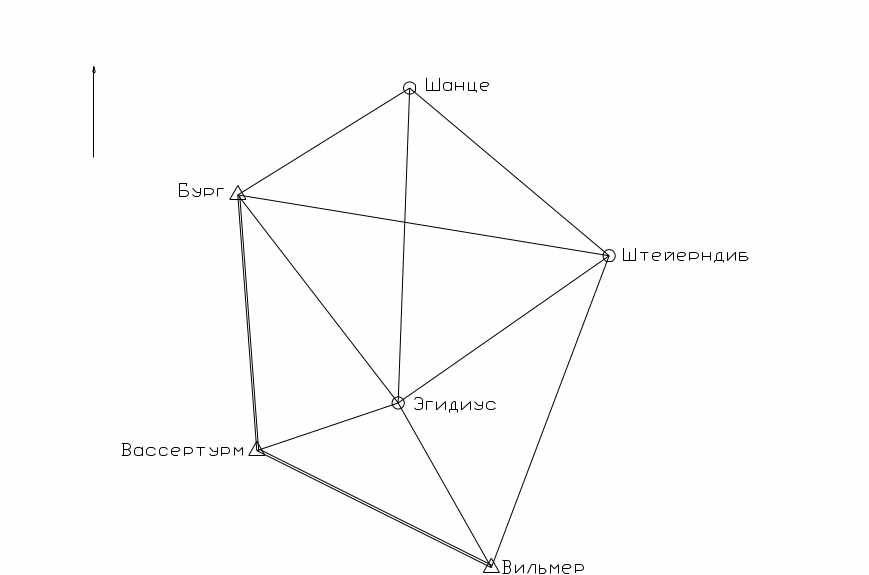
Рис. 3.1 – Схема сети триангуляции

2. Составлен список исходных данных. Координаты исходных пунктов приведены в таблице 3.1, сводка средних приведенных к центру и на плоскость направлений – в таблице 3.2.

Таблица 3.1– Координаты исходных пунктов

Название исходного пункта	Координаты, м
	Х	У
Бург	-24977,399	-25842,799
Вассертурм	-29071,474	-25538,488
Вильмер	-30945,359	-21777,609

Таблица 3.2 – Сводка средних приведенных к центру и на плоскость направлений

Пункт стояния	Пункт визирования	Приведенные и редуцированные на плоскость направления
		градусы	минуты	секунды
Эгидиус	Вассертурм	0	00	00,00
	Бург	70	56	39,31
	Шанце	110	42	26,86
	Штейерндиб	163	44	52,21
	Вильмер	259	04	06,68
Вассертурм	Бург	284	21	18,89
	Эгидиус	0	00	00,00
	Вильмер	45	05	26,74
Вильмер	Вассертурм	326	01	17,37
	Эгидиус	0	00	00,00
	Штейерндиб	50	15	30,53
Штейерндиб	Вильмер	325	34	43,25
	Эгидиус	0	00	00,00
	Бург	44	09	16,56
	Шанце	74	52	34,35
Шанце	Штейерндиб	307	54	59,57
	Эгидиус	0	00	00,00
	Бург	56	04	01,92
Бург	Шанце	275	49	54,13
	Штейерндиб	316	57	21,66
	Эгидиус	0	00	00,00
	Вассертурм	33	24	40,05

Последовательность уравнивания сети триангуляции параметрическим способом

2. В таблицу 3.3 записываем координаты исходных пунктов (Бург, Вассертурм и Вильмер), значения исходных координат пунктов даны по условию и приведены в таблице 3.1. Предварительно полученные координаты определяемых пунктов берем из лабораторной работы № 1 "Предварительные вычисления в триангуляции" из таблицы 1.7. Графы поправки и окончательно уравненные пункты заполняются после выполнения уравнительных вычислений.

Таблица 3.3 – Список координат

№ п/п	Названия пунктов	Приближенные координаты, м		Поправки, м		Окончательные координаты, м
		Х0	У0	Х	У	Х	У
1	Бург					-24977,399	-25842,799
2	Вассертурм					-29071,474	-25538,488
3	Вильмер					-30945,359	-21777,609
4	Шанце	-23266,8	-23087,1	0,090	0,270	-23266,710	-23086,830
5	Эгидиус	-28308,4	-23271,9	-0,031	0,095	-28308,431	-23271,805
6	Штейерндиб	-25952,1	-19888,6	0,164	-0,064	-25951,936	-19888,664

2. В таблице 3.4 приведены жесткие дирекционные углы стороны, которые были вычислены в лабораторной работе № 1 ("Предварительные вычисления в триангуляции") в таблице 1.3.

Таблица 3.4 – Исходные (жесткие) дирекционные углы

Названия сторон	Дирекционные углы 			Стороны S, м
	град	мин	сек
Бург – Вассертурм	175	44	56,56	4105,369
Вассертурм – Вильмер	116	29	06,40	4201,861

Предварительные дирекционные углы вычисляем по приближенным координатам определяемых пунктов и данным координатам исходных пунктов. Вычисления предварительных дирекционных углов и длин сторон приведены в таблице 3.5. Дирекционные углы находим по формулам:

где Х_н,У_н – координаты начального пункта;

Х_к,У_к – координаты конечного пункта;

– табличное значение дирекционного угла.

Таблица 3.5 – Вычисление приближенных дирекционных углов направлений и длин сторон

Сторона н-к	ХК, м ХН, м Х=ХК –ХН, м Х+У, м	УК, м УН, м У=УК -УН, м Х-У, м	tgТ Т 	SК-Н, м
Эгидиус – Вассертурм	-29071,474	-25538,488	2,9703384	2391,6
	-28308,4	-23271,9	710 23' 36" ,88	2391,6
	-763,074	-2266,588	2510 23' 36" ,88
Эгидиус – Бург	-24977,399	-25842,799	-0,7718097	4207,7
	-28308,4	-23271,9	370 39' 40", 71	4207,7
	3331,001	-2570,899	3220 20' 19", 29
Эгидиус – Шанце	-23266,8	-23087,1	0,0366550	5045,0
	-28308,4	-23271,9	20 05' 57",26	5045,0
	5041,600	184,800	20 05' 57",26
Эгидиус – Штейерндиб	-25952,1	-19888,6	1,4358528	4123,0
	-28308,4	-23271,9	550 08' 40",95	4123,0
	2356,300	3383,300	550 08' 40",95
Эгидиус – Вильмер	-30945,359	-21777,609	-0,5666721	3030,9
	-28308,4	-23271,9	290 32' 20" ,46	3030,9
	-2636,959	1494,291	1500 27' 39" ,54

Продолжение табл.3.5

Сторона н – к	ХК, м ХН, м Х=ХК –ХН, м Х+У, м	УК, м УН, м У=УК -УН, м Х-У, м	tgТ Т 	SК-Н, м
Вильмер – Штейерндиб	-25952,1	-19888,6	0,3783118	5338,6
	-30945,359	-21777,609	200 43' 20",00	5338,6
	4993,259	1889,009	200 43' 20",00
Штейерндиб – Бург	-24977,399	-25842,799	-6,1087441	6033,5
	-25952,1	-19888,6	800 42' 11",35	6033,5
	974,701	-5954,199	2790 17' 48",65
Штейерндиб – Шанце	-23266,8	-23087,1	-1,1911146	4176,3
	-25952,1	-19888,6	490 59' 05",53	4176,3
	2685,300	-3198,500	3100 00' 54",47
Шанце – Бург	-24977,399	-25842,799	1,6109556	3243,0
	-23266,8	-23087,1	580 10' 12",27	3243,6
	-1710,599	-2755,699	2380 10' 12",27

При вычислении приближенных дирекционных углов и длин сторон жесткие координаты данных точек не подвергаются округлению, поэтому они берутся такими, какими даны в таблице исходных данных (см. табл. 3.3)

Следует заметить, что вычисления дирекционных углов и длин сторон необходимо производить очень тщательно так, как допущенные ошибки будут обнаружены только в конце уравнительных вычислений.