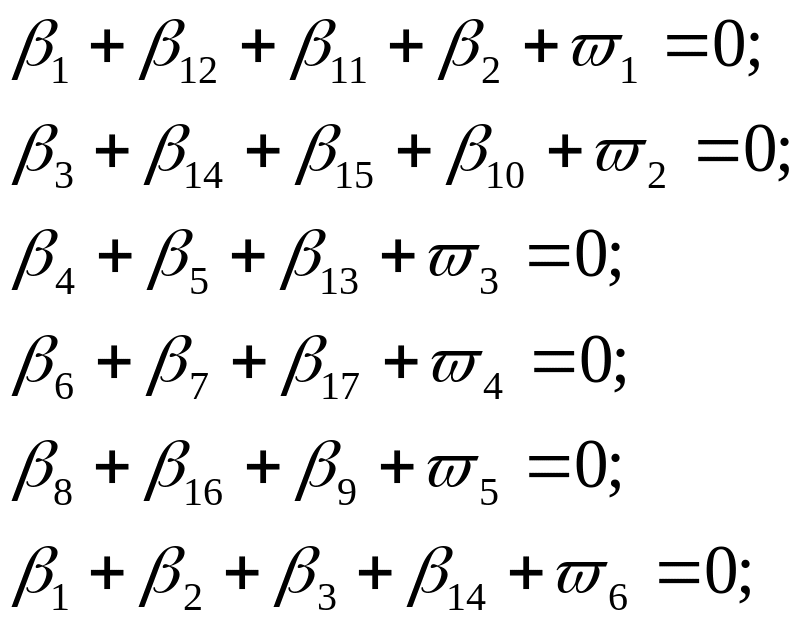8. Оценка точности измеренных углов до производства уравнительных вычислений.

Подсчет числа условных уравнений:

• число условных уравнений (без условий за жесткость):

,

где N – число измеренных углов;

n – число всех пунктов сети (жестких и вставляемых).

• число полюсных (синусных) уравнений:

,

где р – число всех сторон сети (сплошных и несплошных).

• число уравнений горизонта g определяется по схеме сети по количеству точек, вокруг которых измерены все углы.

• число уравнений фигур:

,

• число уравнений за жесткость:

,

где L – число жестких элементов сети.

Для рассматриваемой сети:

число измеренных углов N = 17;

число всех пунктов сети n = 6;

число всех сторон сети р = 11;

число уравнений горизонта g = 1;

число жестких элементов сети L = 6.

Тогда

;

На основании этих формул составляем условные уравнения в общем виде.

Уравнения фигур (таблица 1.13):

Уравнение горизонта (таблица 1.14):

Полюсное уравнение центральной системы Бург-Штейерндиб-Вильмер-Вассертурм полюс Эгидиус (таблица 1.15):

Заменяем длины сторон синусами противолежащих углов.

Полюсное уравнение геодезического четырехугольника Бург-Шанце-Штейерндиб-Эгидиус полюс пункт Бург (таблица 1.16):

Уравнения за жесткость:

уравнение суммы углов (таблица 1.17) –

уравнение стороны (таблица 1.18) – .

Для оценки точности измерения углов вычисляются невязки треугольников, СКО измерения угла, свободные члены условных уравнений.

Величина СКО не должна превышать допусков, установленных инструкцией для соответствующего класса (разряда) триангуляции (см. табл. 1.20).

Минимальная длина стороны треугольника равна 2391,6 м (Вассертурм – Эгидиус), максимальная длина – Бург – Штейерндиб – 6033,0,6 м, средняя длина в рассматриваемой сети составляет 3904,2 м. По данным табл. 1.20:

• допустимая средняя квадратическая ошибка измерения угла – 2",0

• допустимая невязка в треугольнике, не более – 8"

• допустимая СКО базисных сторон 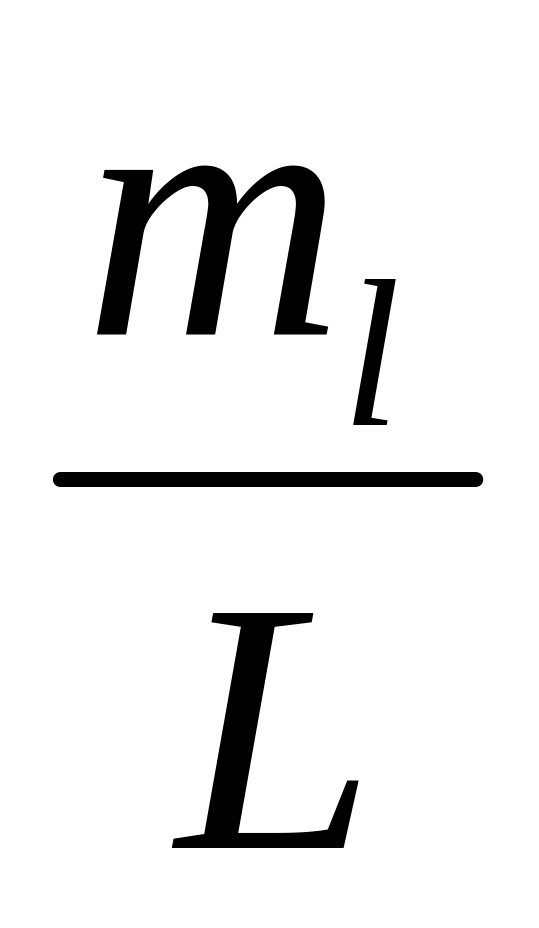, не более – .

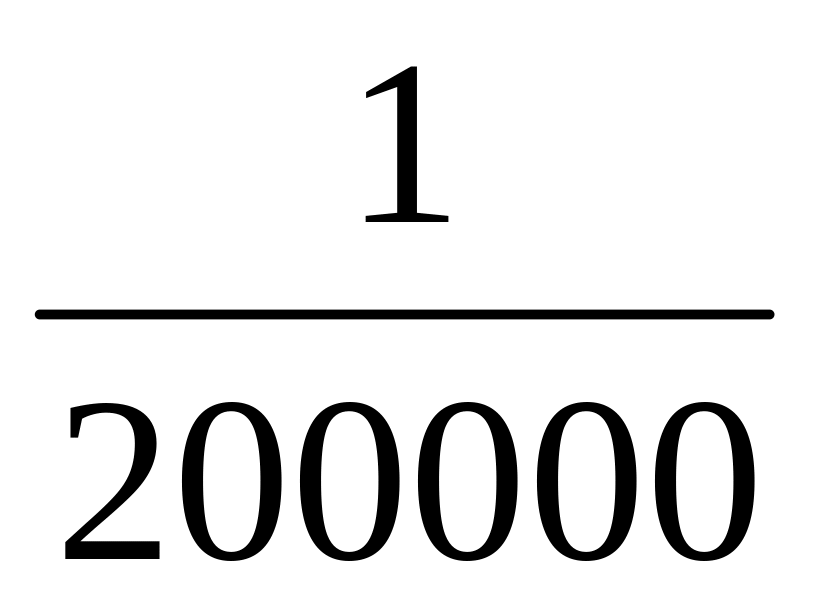Таблица 1.13 – Вычисление невязок треугольников (решение уравнений фигур)

Название вершины	Номер угла	Приведенный угол 			Название вершины	Номер угла	Приведенный угол 
		град	мин	сек			град	мин	сек
Шанце	1+12	108	09	02,35	Эгидиус	17	100	55	53,32
Бург	2	41	07	27,53	Вильмер	7	33	58	42,63
Штейерндиб	11	30	43	17,79	Вассертурм	6	45	5	26,74
 		179	59	47,67 -12,33	 		180	00	02,69 +2,69
Бург	3	43	2	38,34	Штейерндиб	9	34	25	16,75
Штейерндиб	10	44	9	16,56	Эгидиус	16	95	19	30,53
Эгидиус	14+15	92	48	12,90	Вильмер	8	50	15	14,47
 		180	00	07,80 +7,80	 		180	00	01,75 +1,75
Эгидиус	13	70	56	39,31	Шанце	1	56	04	01,92
Бург	4	33	24	40,05	Бург	2+3	84	10	05,87
Вассертурм	5	75	38	41,11	Эгидиус	14	39	45	47,55
 		180	00	00,47 +0,47	 		179	59	55,34 -4,66
Шанце	12	52	05	00,43
Штейерндиб	10+11	74	52	34,35
Эгидиус	15	53	02	25,35
 		180	00	00,13 +0,13

СКО измерения угла вычисляется по формуле Ферреро:

,

где  – невязки в треугольниках;

k – число треугольников.

Подставив значения, получим

,

Таблица 1.14

Уравнение горизонта

Номер угла	Значение приведенного угла
	град	мин	сек
13	70	56	39,31
14	39	45	47,55
15	53	02	25,35
16	95	19	14,47
17	100	55	53,32
 	360	00	00,00 +00,00

Таблица 1.17

Уравнение суммы углов

Наименование	Значение приведенного угла
	град	мин	сек
Бург-Вассертурм	175	44	56,56
5	75	38	41,11
6	45	05	26,74
Вассертурм-Вильмер*	116	29	04,41
Вассертурм-Вильмер 	116	29	06,40 -1,99

Таблица 1.15 – Вычисление свободных членов синусных уравнений

Центральная система Бург – Штейерндиб – Вильмер – Вассертурм (полюс Эгидиус)

№ угла	Приведенный угол 			sin 	lg(sin )		№ угла	Приведенный угол 			sin 	lg(sin )	
	град	мин	сек					град	мин	сек
10	44	9	16,56	0,6965968	-0,1570185	21,8	3	43	2	38,34	0,6825596	-0,1658594	22,5
8	50	15	30,53	0,7689365	-0,1141095	17,3	9	34	25	16,75	0,5652740	-0,2477410	30,6
6	45	5	26,74	0,708226	-0,1498281	21,0	7	33	58	42,63	0,5588819	-0,2526800	31,2
4	33	24	40,05	0,5506428	-0,2591300	32,2	5	75	38	41,11	0,9687771	-0,0137761	5,4
Сумма 1					-0,6800862		Сумма 2					-0,6800565

Невязка: ,

где 1, 2 – соответственно суммы числителя и знаменателя lg(sin );

– изменение логарифмов синусов соответствующих углов на одну секунду.

Допустимая невязка: ,

где – сумма квадратов изменений логарифмов синусов углов треугольников при изменении на 1";

m – установленная инструкцией СКО измеренного угла для соответствующего класса триангуляции.

Невязка .

Допустимая невязка .

Таблица 1.16 – Вычисление свободных членов синусных уравнений

Геодезический четырехугольник Бург – Шанце – Штейерндиб – Эгидиус (полюс Бург)

№ угла	Приведенный угол 			sin 	lg(sin )		№ угла	Приведенный угол 			sin 	lg(sin )	
	град	мин	сек					град	мин	сек
11	30	43	17,79	0,5108672	-0,2916920	35,1	1+12	108	09	2,35	0,9502407	-0,0221664	-6,9
14+15	92	48	12,90	0,9988031	-0,0005201	-1,1	10	44	09	16,56	0,6965968	-0,1570185	21,8
1	56	04	01,92	0,8296929	-0,0810826	13,9	14	39	45	47,55	0,6396162	-0,1940805	25,5
Сумма 1					-0,3732947		Сумма 2					-0,3732654

Невязка: ,

где 1, 2 – соответственно суммы числителя и знаменателя lg(sin );

– изменение логарифмов синусов соответствующих углов на одну секунду.

Допустимая невязка: ,

где – сумма квадратов изменений логарифмов синусов углов треугольников при изменении на 1";

m – установленная инструкцией СКО измеренного угла для соответствующего класса триангуляции.

Невязка .

Допустимая невязка .

Таблица 1.18 – Вычисление свободных членов уравнения стороны

№ угла	Приведенный угол 			sin 	lg(sin ) lg S		№ угла	Приведенный угол 			sin 	lg(sin ) lg S	
	град	мин	сек					град	мин	сек
4	33	24	40,05	0,5506428	-0,2591300	32,2	13	70	56	39,31	0,9452014	-0,0244756	7,1
17	100	55	53,32	0,9818547	-0,0079528	-4,2	7	33	58	42,63	0,5588819	-0,2526800	31,2
SБург-Вассертурм				4105,369	3,6133522		SВассертурм-Вильмер				4201,861	3,6234417
Сумма 1					3,3462694		Сумма 2					3,3462861

Невязка: ,

где 1, 2 – соответственно суммы числителя и знаменателя lg(sin );

– изменение логарифмов синусов соответствующих углов на одну секунду.

Допустимая невязка: ,

где – сумма квадратов изменений логарифмов синусов углов треугольников при изменении на 1";

– СКО логарифма длины базисной стороны или выходной стороны базисной сети;

m – установленная инструкцией СКО измеренного угла для соответствующего класса триангуляции.

Невязка .

Допустимая невязка .