1). На интервале выпукла вниз , 2) на интервале выпукла вверх.

Т ак как касательная в точке является вертикальной прямой, то согласно определению 1.5 точка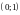 является точкой перегиба графика функции см. рис 7.

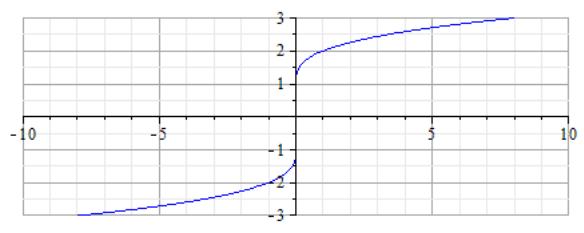
рис.7

Уравнения вертикальных и наклонных асимптот

Рассмотренные выше случаи позволяют исследовать поведение функции в конечной области изменения аргумента. Для изучения поведения функции при стремлении аргумента к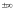 применяются асимптотические формулы.

Определение 1. 7. Наклонная прямая 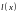= 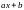называется асимптотой функции пр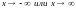и если .

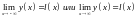Правило 1.3 вычисления невертикальных асимптот функций

Пусть требуется определить и вычислить невертикальную асимптоту = функции . Тогда .

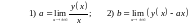Доказательство. Из определения 1. 7 следует, что

1)

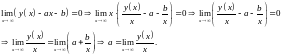
2)

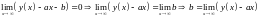
Пример 1.5. Вычислить асимптоты функций .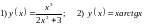

Решение. 1) Применяем правило 1.3. Вычисляем левую асимптоту при

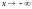
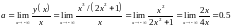
Итак 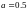. Вычисляем

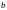
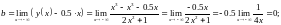
=0. Уравнение левой асимптоты 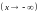равно .

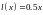Доказать самостоятельно, что уравнение правой асимптоты 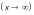равно .

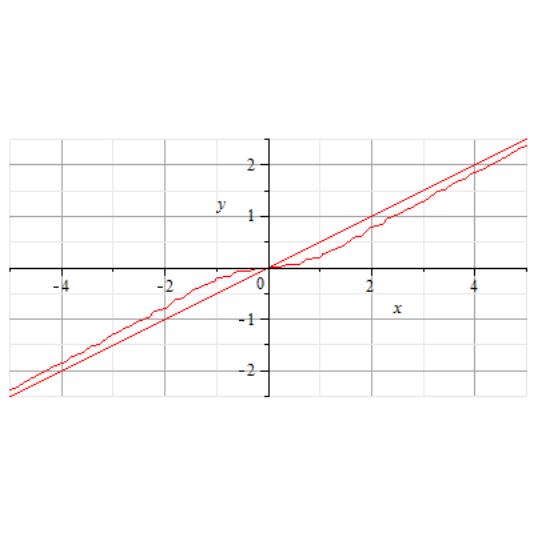
Рис.8

Решение пункта 2) предоставляется читателю.

Напомним определение вертикальной асимптоты графика функции .

Прямая линия 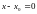называется левой вертикальной асимптотой, если выполняется условие :

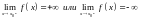(1.5)

Прямая линия называется правой вертикальной асимптотой, если выполняется условие:

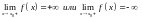(1.6)

Пример 1.6. Найти вертикальную асимптоту функции .

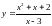Решение. Вертикальные асимптоты могут проходить только через точки разрыва второго рода графика функции. Разрыв графика может быть только в точке 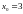. Вычисляем левый и правый пределы функции в точке

Левый предел: .

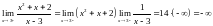Правый предел: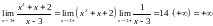

В точке имеем разрыв второго рода. Следовательно, вертикальная асимптота существует и её уравнение имеет вид .

Пример 1.7. Найти левую наклонную асимптоту функции .

Решение. Вычисляем

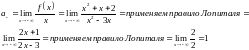
и

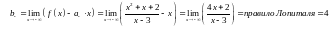Уравнение левой асимптоты имеет вид .

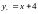Функция 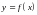имеет правую наклонную асимптоту с уравнением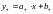

если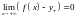 . В этом случае коэффициенты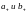 вычисляются по правилу .

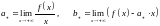Если либо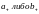 не существуют или равны наклонной асимптоты нет.

Пример 1.8. Найти правую наклонную асимптоту функции .

Решение. Проводим вычисления аналогичные вычислениям примера 2.

Ответ уравнение правой асимптоты имеет вид .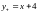

Ответ говорит нам о том , что левая и правая асимптоты совпадают.

Задачи на максимум и минимум в замкнутой области.

Теорема 1.7. Пусть функция 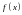непрерывна на отрезке 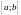. Тогда достигаются либо 1) в критических точках,

либо 2)на концах отрезка.

Доказательство. Так как функция непрерывна на отрезке , то у неё существуют

точки, в которых она достигает максимума и минимума. Если эти значения достигаются не

на концах отрезка, то они располагаются в точках интервала 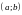. Следовательно, эти точки-

экстремальные , а любая экстремальная точка является критической. Теорема доказана.

Пример 1.8. Найти максимум и минимум функции

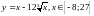
Решение. Вычисляем значения функции на краях отрезка

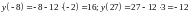
Находим критические точки внутри отрезка :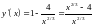

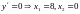. Вычисляем значения функции в этих критических точках.

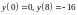. Получаем ответ:

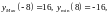
Пример 1.9. Среди всех прямоугольников, вписанных в круг радиуса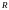 , найти прямоугольник с наименьшей площадью.

Решение. Обозначим основание прямоугольника через , а высоту через 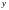. Тогда площадь

прямоугольника вычисляется по формуле 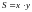. Прямоугольник вписан в круг радиуса R

следовательно, по теореме Пифагора . Таким образом, площадь прямоугольника является функцией переменно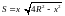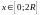й : , . При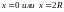 площадь равна нулю. Следовательно, максимум лежит в критической точке функции

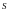
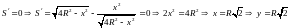
Искомый прямоугольник является квадратом и его площадь равна .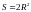

Пример 1.10. Среди всех прямоугольников , имеющих периметр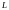 , найти прямоугольник наибольшей площади.

Решение. Обозначим основание прямоугольника через , а высоту через . Тогда периметр

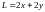прямоугольника вычисляем по формуле . Отсюда вычисляем по формуле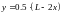 , а площадь прямоугольника равна: ,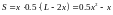

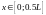
При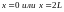 площадь равна нулю. Следовательно, максимум лежит в критической точке функции

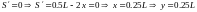
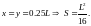
Искомый прямоугольник является квадратом и его площадь равна .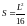

Пример 1.11. Поперечное сечение бревна является кругом радиуса R. Из бревна вырубается брус

С прямоугольным поперечным сечением. Прочность бруса пропорциональна основанию и квадрату высоты поперечного сечения. Найти форму поперечного сечения бруса, при котором прочность максимальна.

Решение. Пусть 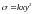, где основание сечения, высота сечения, а k коэффициент пропорциональности зависящий от материала бревна . По теореме Пифагора . Отсюда 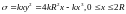. При прочность =0. Следовательно, максимальная прочность может достигаться лишь в критической точке. Отсюда.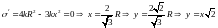

Пример 1.12. Среди всех круговых цилиндров , имеющих объём V , найти размеры цилиндра , имеющего наименьшую площадь поверхности.

Решение. По условию задачи , где радиус основания круга, а 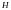высота цилиндра.

Площадь поверхности цилиндра вычисляем по формуле 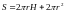. Из формулы объёма

выражаем . Критическую точку для площади находим из уравнения 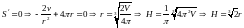.