Лабораторная работа № 12 Тема: Вычисление двойных интегралов

Цели работы:

1. Научиться изменять порядок интегрирования в повторных интегралах.

2. Научиться вычислять двойные интегралы в прямоугольных декартовых координатах.

12.1. Вычисление двойных интегралов в прямоугольной декартовой системе координат

Вычисление двойного интеграла в прямоугольной декартовой системе координат сводится к вычислению повторных интегралов следующим образом. Пусть область D (рис. 3) ограничена кривыми причем всюду на функции и непрерывны и Тогда

,

причём сначала вычисляется внутренний интеграл по переменной ( считается постоянной), потом полученный результат интегрируется по . Интегралы такого вида называются повторными.

Если кривая (или кривая ) в промежутке задается различными аналитическими выражениями, то следует разбить область интегрирования на части и воспользоваться свойством аддитивности интеграла.

Аналогично, можно построить второй повторный интеграл. Если область D ограничена кривыми причем всюду на функции и непрерывны и (рис. 4), то

.

Для двойного интеграла справедливы свойства линейности и аддитивности:

а) линейность:

( - постоянные числа).

б) аддитивность:

если , то .

Чтобы изменить порядок интегрирования в повторном интеграле, необходимо:

1. Определить подынтегральную функцию как функцию переменных и .

2. Задать кривые, ограничивающие область интегрирования в двух видах: выражая как функцию от и, наоборот, как функцию от .

3. Построить на одном графике линии, ограничивающие область интегрирования.

4. Графически определить координаты точек пересечения графиков функций – пределы интегрирования.

5. Найти точное значение координат точек пересечения графиков. Сравнить полученные результаты.

6. Вычислить искомый интеграл, расставив пределы интегрирования (двумя способами).

Пример 1. Изменить порядок интегрирования в повторном интеграле , построить область интегрирования.

Решение. Задаём подынтегральную функцию и определяем границы области интегрирования по пределам повторного интеграла:

Изменим порядок интегрирования. Для этого выразим уравнения границ в виде: :

Область интегрирования разбивается на две части. Исходный интеграл запишется в виде суммы двух интегралов. Вычисляем искомый интеграл двумя способами (используя оба порядка интегрирования) и сравниваем полученные результаты:

Указание. Для того, чтобы задать уравнения границ в виде: или , надо определить границу в виде: и записать функцию Затем в меню «Символика» (Symbolics) выбрать команду «Разрешить относительно переменной» (Variable Solve), выделив сначала или в зависимости от того, какое уравнение хотим получить.

Пример 2. Вычислить двойной интеграл , если область интегрирования ограничена линиями:

Решение. Задаём подынтегральную функцию и определяем кривые, ограничивающие область интегрирования:

Строим область интегрирования:

Найдём точки пересечения графиков функций. Для этого решим систему уравнений:

Система имеет два решения, но из графика видно, что подходит точка с координатами , т.е. − абсцисса точки пересечения графиков функций и . Точка пересечения графиков функций и имеет координаты , а точка пересечения графиков функций и имеет координаты .

Найдём другое выражение для границ области интегрирования (используя меню «Symbolics», команда «Varieble Solve»):

Вычислим двойной интеграл, переходя к повторному интегралу, двумя способами:

Вычислим заданный интеграл аналитически, используя один любой порядок интегрирования (без использования программного продукта MathCAD).

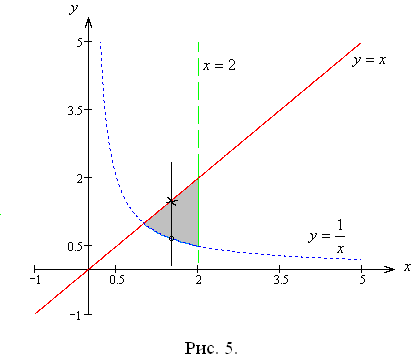
Область интегрирования заштрихована на рис. 5.

Порядок интегрирования выберем следующий: сначала по вдоль любой прямой , проходящей через область , от точки «о» её входа в область в , в которой , до точки выхода « », в которой , затем проведём интегрирование по от крайней левой границы области до правой Имеем: