
- •Лабораторная работа № 8 Тема: Дифференцирование функций нескольких переменных. Экстремум функции двух переменных
- •8.1. Вычисление частных производных
- •8.2. Экстремум функции двух переменных
- •8.3. Условный экстремум функции двух переменных
- •8.4. Задания для самостоятельного решения
- •Лабораторная работа № 9 Тема: Вычисление неопределённых и определённых интегралов
- •9.1. Неопределённый интеграл
- •9.2. Определённый интеграл
- •9.3. Задания для самостоятельного решения
- •Лабораторная работа № 10 Тема: Приложения определённого интеграла к решению геометрических задач
- •10.1. Площадь плоской фигуры
- •10.2. Длина дуги кривой
- •10.3. Задания для самостоятельного решения
- •Лабораторная работа № 11 Тема: Приложения определённого интеграла к решению геометрических задач
- •11.1. Объём тела вращения
- •11.2. Площадь поверхности вращения
- •11.3. Задания для самостоятельного решения
- •Лабораторная работа № 12 Тема: Вычисление двойных интегралов
- •12.1. Вычисление двойных интегралов в прямоугольной декартовой системе координат
- •12.2. Задания для самостоятельного решения
- •Cписок литературы
Лабораторная работа № 11 Тема: Приложения определённого интеграла к решению геометрических задач
Цель работы: Рассмотреть приложения определённого интеграла к решению геометрических задач (вычисление объёмов тел вращения и площади поверхности вращения).
11.1. Объём тела вращения
1.
Рассмотрим криволинейную трапецию,
ограниченную графиком функции
,
прямыми
![]() и осью Ох.
Если эту трапецию вращать вокруг одной
из координатных осей, то получится
некоторое объёмное тело. Объём полученного
тела вращения можно вычислить при помощи
определённого интеграла:
и осью Ох.
Если эту трапецию вращать вокруг одной
из координатных осей, то получится
некоторое объёмное тело. Объём полученного
тела вращения можно вычислить при помощи
определённого интеграла:
-
если трапеция вращается вокруг оси Ох,
то
![]() ;
;
-
если трапеция вращается вокруг оси Оу,
то
![]() .
.
Если
вращается фигура, ограниченная кривыми
![]() и
и
![]()
![]() ,
и прямыми
,
то формулы для вычисления объёма
запишутся соответственно:
,
и прямыми
,
то формулы для вычисления объёма
запишутся соответственно:
![]() и
и
![]() .
.
2. Если фигура, ограниченная кривой, заданной параметрически где , вращается вокруг оси Ох или Оу, то объемы получающихся тел вращения вычисляются по формулам:
 и
и
 .
.
3.
В полярных координатах криволинейный
сектор, ограниченный кривой
и лучами
![]() и
и
![]() ,
можно вращать вокруг полярной оси. Объём
получающегося тела вращения вычисляется
по формуле:
,
можно вращать вокруг полярной оси. Объём
получающегося тела вращения вычисляется
по формуле:
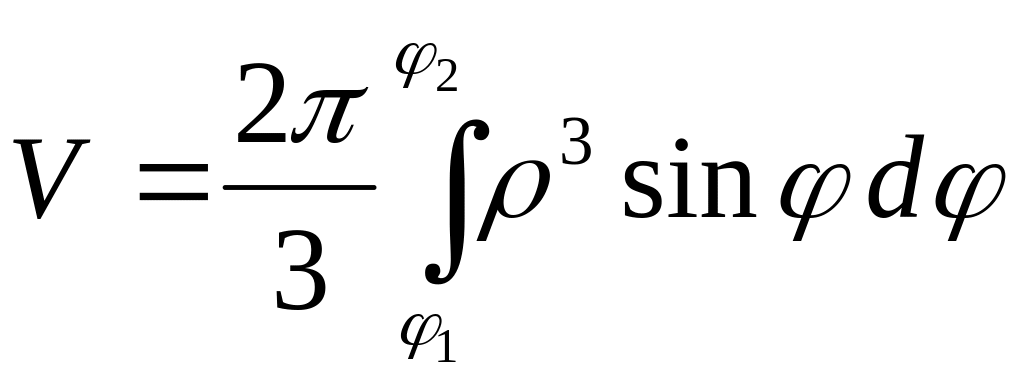 .
.
Пример
1. Найдем
объём тела, образованного вращением
вокруг полярной оси кардиоиды
![]() .
.
Решение. Построим кардиоиду:
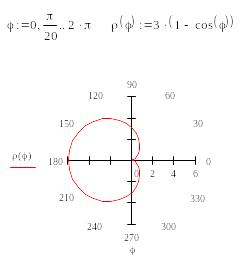
Видим,
что при изменении
от 0
до
![]() получается
фигура, симметричная относительно
полярной оси. Тело вращения получается
при вращении вокруг полярной оси только
одной её части, например, той, что
расположена выше полярной оси. Поэтому
интеграл вычисляем в пределах от 0
до .
получается
фигура, симметричная относительно
полярной оси. Тело вращения получается
при вращении вокруг полярной оси только
одной её части, например, той, что
расположена выше полярной оси. Поэтому
интеграл вычисляем в пределах от 0
до .

11.2. Площадь поверхности вращения
1. Если дуга некоторой кривой , вращается вокруг оси Ох, то получится некоторая поверхность вращения, площадь которой вычисляется по формуле:
![]() .
.
2. Если кривая, заданная параметрически где , вращается вокруг оси Ох , то площадь получающейся поверхности находится по формуле:
 .
.
3. Если кривая, заданная в полярной системе координат уравнением , где , вращается вокруг полярной оси, то площадь получающейся поверхности равна:
 .
.
Пример 2. Найдем площадь поверхности, образованной вращением вокруг оси Ох одной арки циклоиды
Решение. Одна арка циклоиды получается при . Используя соответствующую формулу, вычисляем:
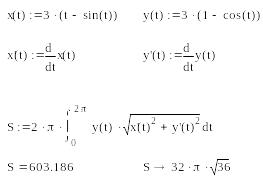
11.3. Задания для самостоятельного решения
1. Вычислить объём тела вращения:
|
а) |
б) |
1. |
|
|
2. |
|
, ось Оу |
3. |
|
, ось Ох |
4. |
|
ось Ох |
5. |
|
|
6. |
|
|
7. |
|
, ось Оу |
8. |
|
ось Ох |
9. |
|
, ось Ох |
10. |
|
, ось Ох |
11. |
|
ось Ох |
12. |
|
полярная ось |
13. |
|
полярная ось |
14. |
|
, ось Оу |
15. |
|
полярная ось |
16. |
|
полярная ось |
17. |
|
полярная ось |
18. |
|
полярная ось |
19. |
, ось Оу |
ось Оу |
20. |
|
полярная ось |
2. Вычислить площадь поверхности вращения:
1. |
|
2. |
|
3. |
|
4. |
|
5. |
|
6. |
|
7. |
|
8. |
|
9. |
|
10. |
|
11. |
|
12. |
|
13. |
|
14. |
|
15. |
, ось Ох |
16. |
|
17. |
|
18. |
|
19. |
|
20. |
|

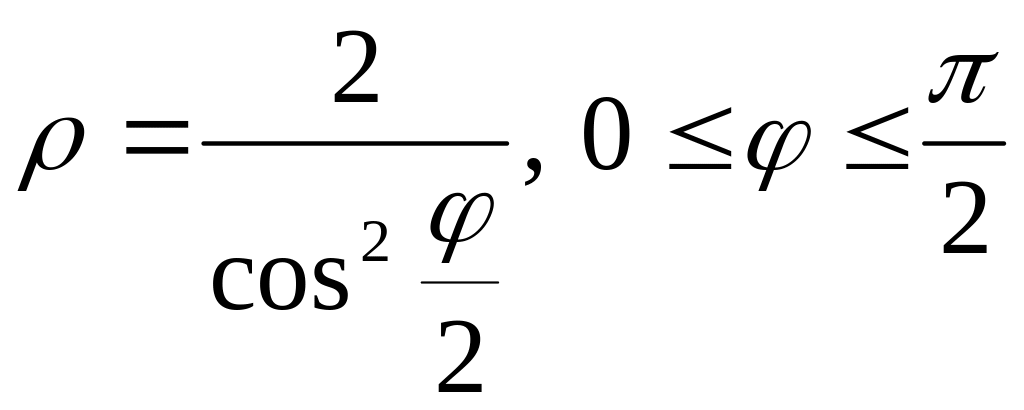 ,
полярная ось
,
полярная ось