Лабораторная работа № 9 Тема: Вычисление неопределённых и определённых интегралов

Цель работы: Научиться вычислять неопределённый и определённый интегралы.

9.1. Неопределённый интеграл

Поскольку в результате вычисления неопределённого интеграла должна получиться функция, то неопределённый интеграл в MathCAD можно вычислить только символьно.

Чтобы вычислить неопределённый интеграл необходимо:

1. Щелкнуть мышью в свободном месте рабочего документа.

2. Вызвать шаблон для вычисления неопределенного интеграла ∫■d■ либо сочетанием клавиш [Ctrl] и [I] , либо используя соответствующую кнопку на палитре «Вычисления».

3. В первом свободном поле указать функцию, от которой вычисляется интеграл, в другом – переменную, по которой производится интегрирование.

4. Вычислить неопределённый интеграл символьно.

Замечание. При вычислении неопределенного интеграла функцию можно задавать предварительно.

Пример 1. Вычислим интеграл .

Решение.

Пример 2. Вычислим интеграл .

Решение.

Обратите внимание, что при вычислении неопределённого интеграла в MathCAD получается не совокупность первообразных (чем по определению является неопределённый интеграл), а лишь одна первообразная, соответствующая значению С=0.

9.2. Определённый интеграл

В большинстве случаев определённый интеграл в Mathcad можно вычислить двумя способами – численно и символьно.

Чтобы вычислить определённый интеграл численно, необходимо:

1. Щелкнуть мышью в свободном месте рабочего документа.

2. Вызвать шаблон для вычисления определенного интеграла ∫■d■ либо клавишей [&] (на английской раскладке), либо используя соответствующую кнопку на палитре «Вычисления».

3. В соответствующих полях указать пределы интегрирования, в первом свободном поле за знаком интеграла указать функцию, от которой вычисляется интеграл, в другом – переменную, по которой производится интегрирование.

4. Набрать знак равенства и щелкнуть мышью вне выражения.

Чтобы вычислить определённый интеграл символьно, необходимо:

1. Щелкнуть мышью в свободном месте рабочего документа.

2. Вызвать шаблон для вычисления определённого интеграла и заполнить его так, как указано выше.

3. Вычислить интеграл символьно (с помощью символьного знака равенства).

Замечание. Так же, как и при вычислении неопределённого интеграла, подынтегральную функцию можно задавать предварительно.

Пример 3. Вычислим двумя способами интеграл .

Решение.

Вычислим интеграл численно:

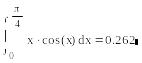
Вычислим интеграл символьно:

Пример 4. Вычислим двумя способами интеграл .

Решение. Зададим предварительно функцию

Вычислим интеграл численно:

Вычислим интеграл символьно:

Отдельно рассмотрим вычисление несобственных интегралов, которые являются обобщением понятия определённого интеграла.

Несобственными интегралами первого рода являются интегралы, у которых один или оба предела интегрирования равны бесконечности. Несобственными интегралами второго рода являются интегралы, у которых одна или несколько точек из промежутка интегрирования являются точками разрыва подынтегральной функции. Несобственные интегралы бывают сходящимися (если в результате вычислений получаем конечное число) или расходящимися (в противном случае).

В MathCAD несобственные интегралы вычисляются так же, как определённые: численно или символьно. Однако некоторые несобственные интегралы вычисляются либо только символьно, либо только численно.

Пример 5. Вычислим несобственный интеграл первого рода .

Решение.

Вычислим интеграл численно:

Вычислим интеграл символьно:

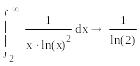
Пример 6. Вычислим несобственный интеграл 2-го рода .

Решение.

Вычислим интеграл численно:

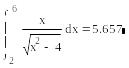
Вычислим интеграл символьно: