8.3. Условный экстремум функции двух переменных

Кроме экстремума в точке, для функции двух переменных рассматривается условный экстремум, т. е. экстремум функции , найденный в предположении, что переменные х и у связаны соотношением , которое называется уравнением связи.

Задача нахождения условного экстремума сводится к исследованию на экстремум функции Лагранжа .

Необходимое условие условного экстремума выражается системой:

Пусть , - некоторое решение этой системы.

Достаточное условие условного экстремума. Вычислим определитель

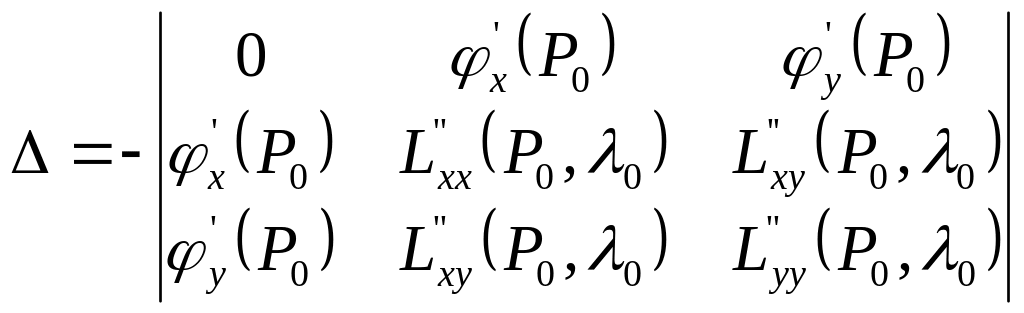Если , то функция имеет в точке условный минимум; если , то функция имеет в точке условный максимум.

Пример 8. Найдем условный экстремум функции при условии .

Решение. Составим функцию Лагранжа и найдем частные производные первого порядка:

Система уравнений

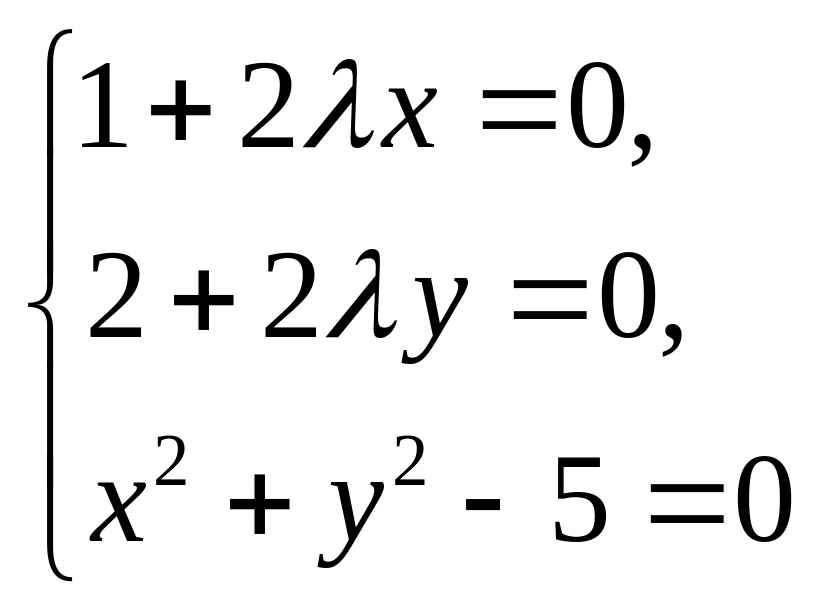
имеет два решения: и .

Вычислим для каждого решения.

Т.к. , то в точке функция имеет условный минимум, равный .

8.4. Задания для самостоятельного решения

1. Найти частные производные первого и второго порядков:

1.	а) б)	11.	а) б)
2.	а) б)	12.	а) б)
3.	а) б)	13.	а) б)
4.	а) б)	14.	а) б)
5.	а) б)	15.	а) б)
6.	а) б)	16.	а) б)
7.	а) б)	17.	а) б)
8.	а) б)	18.	а) б)
9.	а) б)	19.	а) б)
10.	а) б)	20.	а) б)