Лабораторная работа № 8 Тема: Дифференцирование функций нескольких переменных. Экстремум функции двух переменных

Цели работы:

1. Научиться вычислять производные первого и высших порядков для функций нескольких переменных.

2. Научиться находить экстремум функции двух переменных.

8.1. Вычисление частных производных

Производные для функций нескольких переменных, так же как и для функций одной переменной, можно вычислять символьно и численно.

Последовательность действий при вычислении производных первого порядка функции нескольких переменных точно такая же, как и при вычислении производных для функции одной переменной, с тем лишь отличием, что функция теперь содержит не одну, а несколько переменных, и производная по каждому аргументу находится отдельно.

Пример 1. Вычислим значение частных производных от функции в точке (-1; 2).

Решение.

Пример 2. Вычислим значение частных производных функции в точке (1; 2; -3).

Решение.

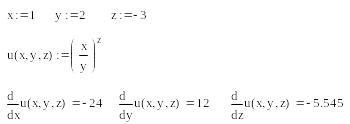
Пример 3. Найдем частные производные для функции .

Решение.

Рассмотрим теперь вычисление производных высших порядков для функции нескольких переменных. Функции нескольких переменных можно дифференцировать несколько раз по одной и той же переменной или по различным переменным. Напомним, что в последнем случае результат дифференцирования не зависит от последовательности дифференцирования.

Если необходимо найти производную порядка п по одной и той же переменной, то поступают также, как при нахождении производной порядка п для функции одной переменной.

Если необходимо найти «смешанную» производную, то дифференцирование производят последовательно. При этом шаблоны для производных можно «вкладывать» один в другой (каждый последующий шаблон вызывается в том поле, где должна вводиться функция).

Пример 4. Найдем значения производных второго порядка от функции в точке (1; -2).

Решение.

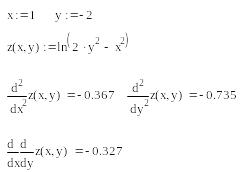
Пример 5. Найдем производные второго порядка для функции:

.

Решение.

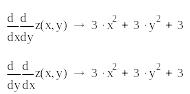
Пример 6. Для функции убедиться, что .

Решение.

Совпадение результатов дифференцирования позволяет убедиться в справедливости записанного равенства.

8.2. Экстремум функции двух переменных

Функция имеет максимум (минимум) в точке , если существует такая окрестность точки Р₀ , для всех точек Р(х, у) которой, отличных от точки Р₀ , выполняется неравенство (соответственно ). Точки минимума и максимума функции называются точками экстремума этой функции.

Необходимое условие экстремума. Если дифференцируемая функция имеет экстремум в точке , то в этой точке

Т.е. если - точка экстремума функции , то либо частные производные в этой точке равны нулю (в этом случае точку называют стационарной точкой), либо функция в этой точке не является дифференцируемой.

Достаточное условие экстремума. Пусть - стационарная точка функции , причем эта функция дважды дифференцируема в некоторой окрестности точки Р₀ и все ее вторые производные непрерывны в точке Р₀. Вычислим

.

Тогда:

- если , то функция имеет в точке экстремум: максимум при (или при ), минимум при (или при );

- если , то в точке экстремума нет;

- если , то требуется дополнительное исследование.

Пример 7. Исследуем на экстремум функцию .

Решение. Найдем частные производные первого порядка:

Решив систему уравнений

найдем две стационарные точки .

Найдем значения частных производных второго порядка и вычислим в точке :

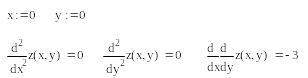
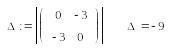
Т.к. в точке , то экстремума в этой точке нет.

Найдем значения частных производных второго порядка и вычислим в точке :

Т.к. в точке и , то в точке функция имеет минимум, равный