Қ
АЗАҚСТАН
РЕСПУБЛИКАСЫНЫҢ БІЛІМ ЖӘНЕ ҒЫЛЫМ
МИНИСТРЛІГІ
Жәңгір хан атындағы Батыс Қазақстан аграрлық-техникалық университеті
Агрономия, ветеринарлық медицина және биотехнология факультеттерінің 5В072700 – «Азық-түлік өнімдерінің технологиясы», 5В072800 – «Қайта өңдеу өндірістерінің технологиясы», 5В070100 – «Биотехнология»
мамандықтарының1 курс студенттеріне арналған
«Математика 1»
Өзіндік жұмыс материалдары
Орал – 2011ж.
Құрастырушылар:
аға оқытушылар Рамазанова Э.М., Нургазинова М.К.,
оқытушы Жумажанова И.А.
«Физика және математика» кафедрасы
Политехникалық факультет, аудитория №201.
Кредит саны – 3
Өзіндік жұмыс – 65 сағат
Кафедра отырысында талданды «26» тамыз 2011ж. Хаттама №1.
Білім алушыларға арналған өзіндік жұмыс материалдары
Жеке тапсырма №1. (2 апта)
Тақырыбы: «СТЖ және матрицаға амалдар қолдану»
Мақсаты – анықтауыштар ұғымын енгізу, меңгеру және кері матрицаны есептеу ережесі.
Тапсырма |
Балл |
|
Есеп №1. Теңдеулер жүйесін әдіспен шешу Есеп №2. Төрт белгісізі бар теңдеулер жүйесін Гаусс әдісімен шешу. |
Крамер әдісімен
|
50 |
Гаусс әдісімен |
50 |
|
Есеп №3. Матрицаларға амалдар |
А) Матрицаны транспонирлеңіз В) Матрицаның рангісін табыңыз. С) Кері матрицаны табыңыз. Д) Үш белгісізі бар теңдеулер жүйесін матрицалық әдіспен |
100 |
Барлығы: |
200 |
|
Вариант№1.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
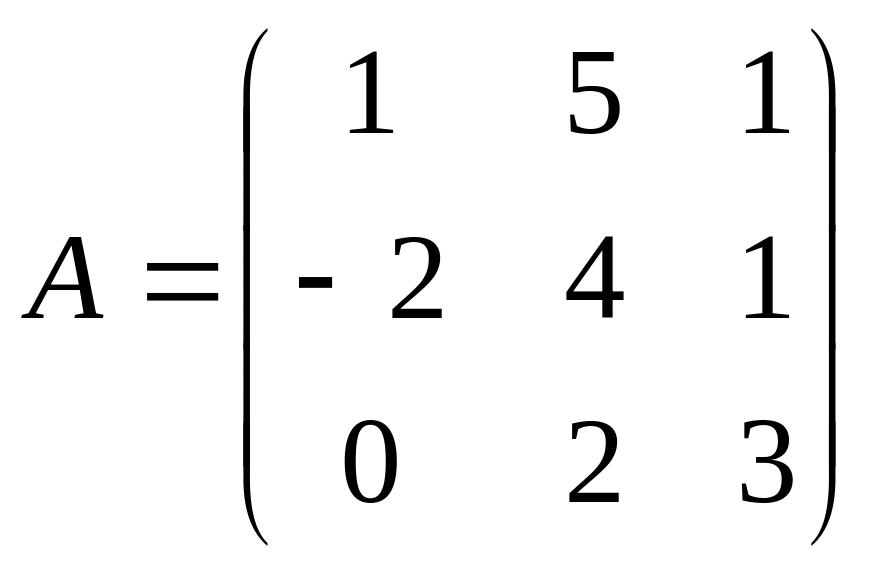; В)
; С)
Вариант№2.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
;
В)
;
С)
Вариант№3.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№4.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
;
С)
Вариант№5.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№6.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
;
С)
Вариант№7.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№8.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№9.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№10.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№11.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№12.
Есеп
№1. 
Есеп
№2. 
№3. А)
; В)
; С)
Вариант№13.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№14.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№15.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№16.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№17.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№18.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№19.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Вариант№20.
Есеп
№1. 
Есеп
№2. 
Есеп
№3. А)
; В)
; С)
Әдебиеттер: 8,11,16, 23,24,28.
Жеке тапсырма №2.
Тақырыбы: «Векторлық есептеулер» (3 апта)
Мақсаты: – векторлық есептеулердің қолданылуын меңгеру және аналитикалық геометрияның есептерін шығару әдістері.
А,
В, С, А
нүктелері координаталарымен берілген.
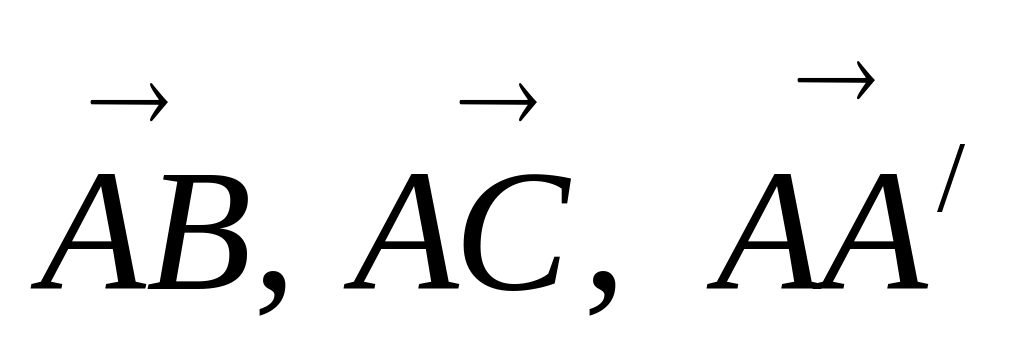векторларын
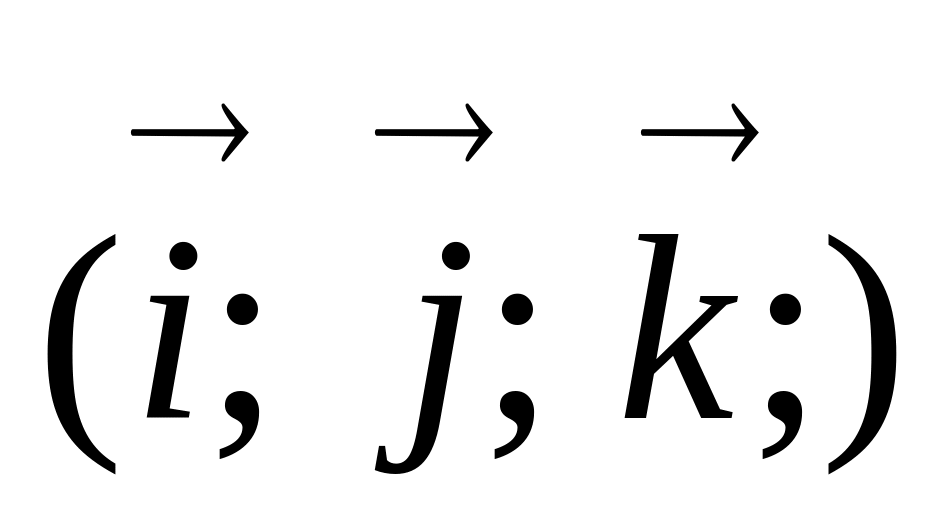жүйесінде өрнектеңіз,осы векторлардың
модулін табыңыз.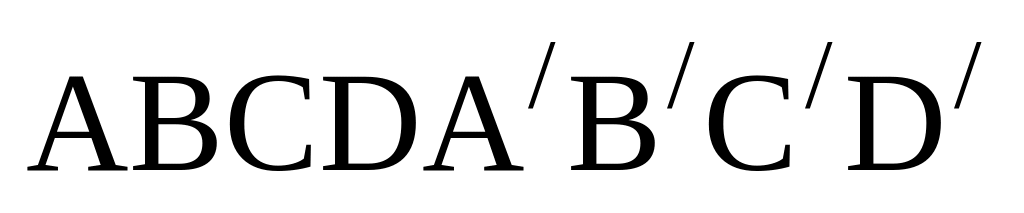
параллелопипедінің
табаны АВСД болатындай Д (х, у, z)
нүктесінің координатасын және cos
;
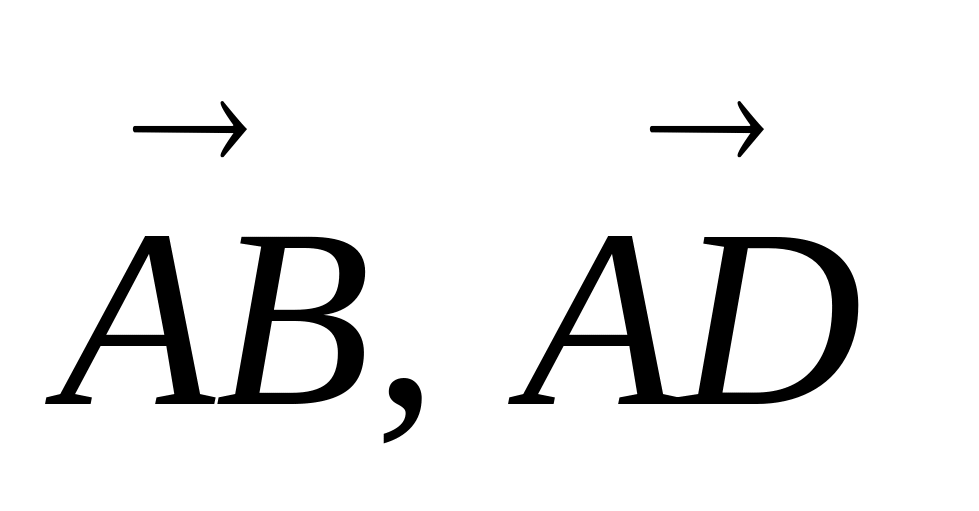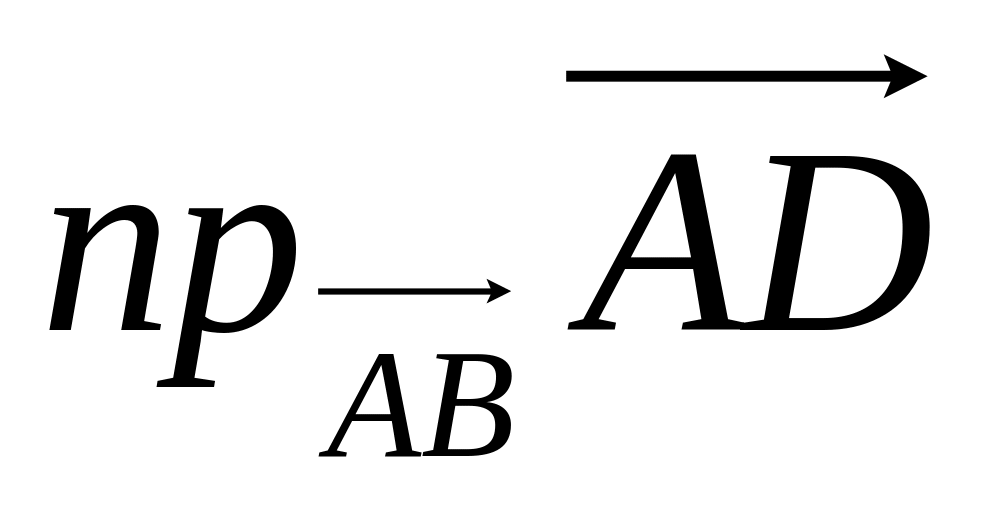табыңыз.
векторлары
жазықтықта, ал
векторлары кеңістікте базис құрай ма?векторлары арқылы тұрғызылған АВСД параллелограмының және параллелопипедінің көлемін табыңыз.
№ |
|
|
|
|
|
|
(2, 0, 0) |
(0, 2,0) |
(0, 0, 2) |
(0, 0, 6) |
|
|
(3, 0,0) |
(0, 3, 0) |
(0, 0, 3) |
(0, 0, 6) |
|
|
(-2, 0,0) |
(0, 2,0) |
(0, 0, 2) |
(0, 0, 6) |
|
|
(-3, 0,0) |
(0, 3, 0) |
(0, 0, 3) |
(0, 0, 8) |
|
|
(2, 2, 0) |
(0, 2, 2) |
(2, 0, 2) |
(0, 0, 8) |
|
|
(2, -2,0) |
(0, 2, 2) |
(0, -2, 2) |
(0, 0, 8) |
|
|
(3, -3,0) |
(0, 0, 3) |
(0, -3, 0) |
(0, 0, 9) |
|
|
(4, -4,0) |
(0, 4, 4) |
(6, -4, 4) |
(0, 0, -4) |
|
|
(2, -2, 0) |
(0, -2, 2) |
(-2, 0,0) |
(0, 0, 4) |
|
|
(3, -3, 0) |
(0, 3, 3) |
(-3, 0, 0) |
(0, 0, 5) |
|
|
(4, -4, 0) |
(0, -4, 4) |
(-4, 0,0 ) |
(0, 0, 6) |
|
|
(5, -5, 0) |
(0, -5, 5) |
(-5, 0, 0) |
(0, 0, 7) |
|
|
(0, 0, 3) |
(0, -3, 4) |
(-3, 0, 0) |
(0, 0, 5) |
|
|
(0, 0, 4) |
(0, -4, 5) |
(-4, 0, 0) |
(0, 0, 6) |
|
|
(0, 0, -3) |
(0, 3, 0) |
(0, 0,3) |
(-3, 3, 5) |
|
|
(3, -5, 0) |
(0, -3, 3) |
(3, 0,0) |
(-3, -3, 5) |
|
|
(3, -5, 0) |
(0, -3, 3) |
(0, 0, 3) |
(0, 0, 6) |
|
|
(1, -1, 0) |
(0, 1, 1) |
(0, -1, 1) |
(0, 0, 5) |
|
|
(-5, 0,0) |
(0, 5, 0) |
(0, 0, 5) |
(0, 0, 7) |
|
|
(0, 1, 0) |
(2, 1, 0) |
(3, 0, 0) |
(0, 0, -4) |
