Учебно-методическое пособие функциональные последовательности и ряды. Ляхов л. Н. Мешков в.З. Половинкин и.П. Половинкина м.В. Попков а.В. Шишкина э.Л.
Утверждено научно-методическим советом факультета ПММ
__.__.201__, протокол №__.
Рецензент д.ф.-м. н., профессор Каменский : _________________.
Учебно-методическое пособие подготовлено на кафедре математического и прикладного анализа факультета ПММ Воронежского государственного университета.
Рекомендуется для студентов 1 курса дневного отделения факультета ПММ.
Для специальностей: 010200 – Прикладная математика и информатика,
010500 – Механика,
010503 – Математическое обеспечение и администрирование информационных систем
Поточечная и равномерная сходимость функциональных последовательностей и рядов. Критерий Коши о равномерной сходимости. Необходимое условие равномерной сходимости функционального ряда.
Объектами наших
исследований будут функциональные
последовательности, то есть
последовательности функций
,
определенных на
одном и том же
множестве
D,
и функциональные ряды, то есть ряды вида
,
члены которых – функции
,
определенные на
одном и том же множестве
D.
Определение.
Пусть функции
(члены функционального ряда – функции
),
n=1,2,…, определены на множестве D
и пусть
.
Если числовая
последовательность
(числовой ряд
)
сходится, то говорят, функциональная
последовательность
(функциональный ряд
)
сходится в точке
.
Если функциональная последовательность
(функциональный ряд
)
сходится в каждой точке
к некоторому значению f(x), то говорят,
что она (он) сходится к функции f(x)
поточечно на множестве D.
Функцию f(x) называют предельной функцией
последовательности
(суммой функционального ряда
).
При этом используются следующие записи:
.
Согласно определениям предела числовой последовательности и суммы числового ряда эти записи соответственно означают, что
-
для функциональной последовательности
(
- для функционального ряда).
Отметим, что номер
в этих определениях подбирается после
произвольного задания точки
и сколь угодно малого числа
,
а поэтому зависит от х
и .
Пример 1. Найти
предельную функцию f(x)
функциональной
последовательности
на множестве [0,1].
Решение. Если
,
то
а если
то
.
Следовательно, предельная функция имеет
вид
Пример 2. Найти
предельную функцию f(x)
функциональной
последовательности
на множестве
.
Решение.
Используя первый замечательный предел,
который имеет вид
,
получим
Таким образом,
предельная функция имеет вид
.
Для нахождения области сходимости функционального ряда при фиксированном значении х можно использовать необходимый признак сходимости числового ряда, признаки сходимости знакоположительных числовых рядов (признаки Даламбера, Коши, интегральный и др.) и признак Лейбница для знакочередующихся рядов.
Пример 3. Определить
область сходимости (абсолютной и
условной) функционального ряда
.
Решение.
Исследуем
ряд на абсолютную сходимость. Для этого
рассмотрим ряд
,
общий член которого имеет вид
При фиксированном значении х
применим признак Даламбера сходимости
знакоположительного числового ряда
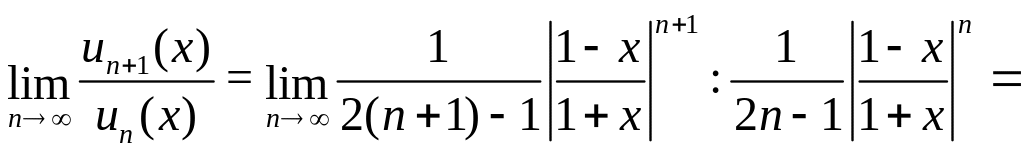
Таким
образом, для сходимости этого ряда
необходимо, чтобы
.
Решая это неравенство, получаем
.
Следовательно, ряд сходится абсолютно
при
.
Если
,
то
и
Получаем знакочередующийся ряд
.
Исследуем его на сходимоть, применяя
признак Лейбница:
1.
для всех натуральных n,
т.е. модули членов исследуемого ряда
образуют убывающую последовательность;
2.
.
Все условия признака Лейбница выполнены, следовательно ряд сходится (сходится неабсолютно).
Поэтому исходный ряд сходится абсолютно при и условно при .
При
ряд
расходится,
так как не выполнено необходимое условие
сходимости: общий член ряда не стремится
к нулю при
.
Действительно, при
получаем, что
При фиксированном
пусть
Тогда имеем
Последнее
утверждение
можно
показать,
например, по правилу Лопиталя:
Пример 4. Определить
область сходимости (абсолютной и
условной) функционального ряда
Решение.
Функции
определены при
Для исследования ряда на абсолютную
сходимость используем интегральный
признак. При фиксированном х
имеем
1. Функция
неотрицательна. Неравенство
справедливо
только когда p>0,
поэтому функция
убывает (по переменной у)
на
промежутке
при p>0.
2. Интеграл
сходится
абсолютно, если
.
Таким
образом, ряд
сходится абсолютно при
и
,
Исследуем ряд на условную сходимость, применяя признак Лейбница.
1.
при
.
2.
при
и
,
.
Следовательно,
ряд
сходится
абсолютно
при
,
,
и условно при
,
,
.
Определение. Говорят, что функциональная последовательность (функциональный ряд ) равномерно сходится на множестве D к функции f(x), если выполнено следующее условие:
для функциональной
последовательности (
- для функционального ряда).
Если функциональная последовательность (функциональный ряд) сходится равномерно на множестве D, то используют следующие записи:
В этом определении
существенно, что номер
подбирается уже после задания числа
и не зависит от точки
.
Пусть
- остаток функционального ряда порядка
n.
Тогда введенное в определении условие
равномерной сходимости функционального
ряда равносильно условию
Это соображение будет использовано
нами в дальнейшем.
Пример 5. Доказать,
что функциональный ряд
равномерно сходится на множестве
.
Решение.
Общий член ряда имеет вид
.
Ипользуя формулу суммы первых n
членов геометрической прогрессии,
найдем n-ю
частичную сумму ряда
и
сумму ряда f(x):
Здесь мы учли, что
так как
.
Подставив полученные результаты в
определение равномерно сходящегося
ряда, получим
,
поскольку
.
Следовательно, ряд
сходится к своей сумме
равномерно на отрезке
:
.
Пример 6. Доказать,
что функциональный ряд
равномерно сходится на множестве
.
Решение. Заметив, что
найдем и f(x):
Теорема (критерий
Коши равномерной сходимости функциональной
последовательности и функционального
ряда). Для
того, чтобы функциональная последовательность
(функциональный
ряд
)
равномерно сходилась (сходился) на
множестве D, необходимо и достаточно,
чтобы выполнялось следующее условие
Коши:
- для функциональной последовательности
;
- для функционального ряда
Доказательство. Докажем сначала теорему для функциональной последовательности.
Необходимость.
Пусть
.
Тогда по определению равномерной
сходимости
Поскольку при
также справедливо и неравенство
,
то будет выполняться и неравенство
Отсюда при получаем
то есть выполняется условие Коши.
Достаточность.
Пусть выполнено условие Коши. Тогда для
каждой точки
числовая последовательность
является фундаментальной, а значит,
согласно критерию Коши сходимости
числовой последовательности, сходится.
Поэтому функциональная последовательность
по крайней мере поточечно сходится к
некоторой функции f(x)
на множестве D. Докажем, что на самом
деле эта сходимость является равномерной
на множестве D. Запишем условие Коши в
виде
Перейдем в этом
неравенстве при каждом фиксированном
номере
и каждой фиксированной точке
к пределу при
.
Учитывая, что
,
по теореме о переходе к пределу в
неравенствах получим:
Это и означает равномерную сходимость последовательности к функции f(x) на множестве D.
В случае функциональных
рядов достаточно заметить, что для
частичных сумм
справедливо следующее тождество на
множестве D:
Далее можно применить доказанное утверждение для функциональных последовательностей.
Теорема доказана.
Приведем примеры использования критерия Коши для исследования равномерной сходимости функциональных последовательностей и рядов.
Критерий равномерной сходимости функциональной последовательности в терминах супремума модуля разности между членами последовательности и предельной функцией. Критерий равномерной сходимости функционального ряда в терминах супремума модуля остатка.
Докажем критерии равномерной сходимости функциональных последовательностей и рядов, непосредственно вытекающие из определения равномерной сходимости.
Теорема.
Для того,
чтобы последовательность функций
,
определенных на множестве D, равномерно
на множестве D сходилась к функции f(x),
необходимо и достаточно, чтобы выполнялось
следующее условие:
Доказательство.
Введем числовую последовательность
.
Тогда условие теоремы по определению
предела числовой последовательности
означает, что выполняется условие
Если , то по определению равномерной сходимости имеем:
Переходя к точной верхней грани в последнем неравенстве, получаем:
,
что и требовалось. Обратно, если выполняется условие теоремы, то мы получим
то есть .
Теорема доказана.
Следствие. Для того, чтобы функциональный ряд равномерно сходился на множестве D, необходимо и достаточно, чтобы выполнялось условие
где
- остаток ряда порядка n.
Доказательство.
Поскольку для равномерной сходимости
функционального ряда необходимо и
достаточно, чтобы выполнялось условие
,
осталось применить доказанную теорему.