Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 7»
Бавлинского муниципального района Республики Татарстан
УЧЕБНЫЕ ЗАДАНИЯ
ПО ГЕОМЕТРИИ 7 КЛАССА
Учитель математики высшей
квалификационной категории
Шамсиева Гузель Варисовна
г. Бавлы
2013 год
I ЛИСТ ВЗАИМОКОНТРОЛЯ
7 КЛАСС
ГЕОМЕТРИЯ
Вопросы
1.Что изучает геометрия?
2.Что изучает планиметрия?
3.Основные геометрические фигуры на плоскости.
4.Обозначение точек и прямых.
5
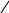.Знаки
є и є. Как прочитать записи А є а, В є а?
6.Как описать рисунок?
7.Аксиома.
8.Теорема.
9.Определение.
10.Аксиома I. Что выражает эта аксиома?
11.Свойства прямой.
12.Отрезок. Обозначение отрезков.
13.Свойства отрезков.
14. Аксиома откладывания отрезков.
15. Аксиома измерения отрезков.
16. Луч (или полупрямая). Обозначение луча.
17. Дополнительные лучи.
18. Угол. Обозначение угла.
19. Развернутый угол. Прямой угол.
20. Свойства углов.
21. Аксиома откладывания углов.
22. Аксиома измерения углов.
23. Треугольник. Внешний угол треугольника.
24. Равные треугольники.
25. Параллельные прямые.
26. Аксиома параллельных прямых.
27.Смежные углы.
28.Свойство смежных углов.
29.Виды углов.
30.Вертикальные углы.
31.Свойство вертикальных углов.
32.Перпендикулярные прямые.
33.Свойство двух прямых, перпендикулярных третьей.
34.Биссектриса.
35.Признаки равенства треугольников.
36. Равнобедренный треугольник и его свойство.
37. Высота.
38. Медиана.
39. Биссектриса треугольника.
40. Свойства медианы, биссектрисы и высоты равнобедренного треугольника.
41. Свойство двух прямых, параллельных третьей.
42. Углы при параллельных и секущей.
43. Признаки параллельности прямых.
44. Свойства накрест лежащих, соответственных и внутренних односторонних углов.
45. Сумма углов треугольника.
46. Следствия из теоремы о сумме углов треугольника.
47. Признаки равенства прямоугольных треугольников.
48. Теорема о единственности опущенного перпендикуляра.
49.Окружность. Хорда. Диаметр. Радиус. Сектор. Сегмент. Круг.
50. Центральный угол.
51. Вписанный угол.
52. Свойства центрального и вписанного углов.
53. ГМТ.
54. Касательная к окружности.
55. Окружность, вписанная в треугольник.
56. Окружность, описанная около треугольника.
57. Замечательные точки треугольника.
I лист взаимоконтроля
7 Класс геометрия
Ответы
Геометрия изучает геометрические фигуры и их свойства.
Планиметрия изучает геометрические фигуры и их свойства на плоскости.
Основные геометрические фигуры на плоскости – это точка и прямая.
Точки обозначают большими латинскими буквами: A,B,C,D,...,прямые - маленькими латинскими буквами: a,b,c,d,... .
Точка А лежит на прямой а , или точка А принадлежит прямой а, или прямая проходит через точку А; точка В не лежит на прямой а ,или точка В не принадлежит прямой а, или прямая проходит через точку В.
Прямые а и b пересекаются в точке С; точка А принадлежит прямой а, но не принадлежит прямой b ; точка В принадлежит прямой b, но не принадлежит прямой а; точка D не принадлежит ни прямой а, ни прямой b.
Аксиома - это истина, которая принимается без доказательства.
Теорема - это истина, которую необходимо доказать.
Дать определение чему-либо - это значит объяснить, что это такое.
Аксиома I.
Через любые две точки можно провести прямую, и только одну. Эта аксиома выражает одно из свойств прямой.
Свойства прямой.
Прямая в обе стороны бесконечна.
Через две точки можно провести прямую, и только одну.
Две прямые пересекаются только в одной точке. Доказать.
Отрезок - это часть прямой, ограниченная двумя точками. Эти точки называются концами отрезка. Отрезки обозначают двумя большими латинскими буквами.
Свойства отрезков.
- Равные отрезки имеют равные длины.
- Меньший отрезок имеет меньшую длину.
Аксиома измерения отрезков.
Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Аксиома откладывания отрезков.
На любом луче можно отложить отрезок, равный данному, и притом только один.
Проведем прямую а и отметим на ней точку О. Эта точка разбивает прямую на две части, каждая из которых называется лучом, исходящим из точки О. Обычно луч обозначают либо малой латинской буквой, либо двумя большими латинскими буквами, первая из которых обозначает начало луча, а вторая – какую-нибудь точку на луче.
Дополнительные лучи – это лучи, которые лежат на одной прямой и имеют общее начало.
Угол – это фигура, состоящая из точки и двух различных лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало – вершиной угла.
Развернутый угол – это угол, сторонами которого являются дополнительные лучи. Прямой угол – это половина развернутого угла.
Свойства углов.
Равные углы имеют равные градусные меры, меньший угол имеет меньшую градусную меру, прямой угол равен 90 градусов, развернутый угол равен 180 градусам.
Аксиома откладывания углов.
От любого луча в заданную полуплоскость можно отложить угол, равный данному, и только один.
Аксиома измерения углов.
Величина угла равна сумме величин углов, на которые он разбивается любым лучом, выходящим из его вершины.