
- •Трофимов в.Г. Методические указания по линейной алгебре (определители, матрицы и системы линейных уравнений)
- •1. Определители
- •1.1 Определители второго и третьего порядков
- •1.2 Свойства определителей
- •2) Все свойства выполняются для определителей любого порядка.
- •Примеры для самостоятельного решения.
- •1.3. Определители высших порядков
- •Примеры для самостоятельного решения.
- •2. Матрицы
- •2.1. Линейные действия с матрицами.
- •Примеры для самостоятельного решения.
- •2.2. Умножение матриц.
- •Примеры для самостоятельного решения.
- •2.3 Обратная матрица.
- •Примеры для самостоятельного решения.
- •3. Системы линейных уравнений.
- •3.1. Формулы Крамера.
- •1) Формулы (3.2) не имеют смысла;
- •2) Система может иметь бесчисленное множество решений или не иметь решений (быть несовместной);
- •3) Исследование системы может быть проведено по методу Гаусса.
- •Примеры для самостоятельного решения.
- •3.2.Решение систем методом обратной матрицы.
- •Примеры для самостоятельного решения. Решить системы с помощью обратной матрицы
- •3.3 Решение систем линейных уравнений методом исключения неизвестных (методом Гаусса). Карл Фридрих Гаусс ( 1777-1855 ), немецкий математик.
- •1)Прибавление к обеим частям одного уравнения соответствующих частей другого уравнения той же системы, умноженных на одно и то же число, не равное нулю.
- •2)Перестановка уравнений местами.
- •3)Удаление из системы уравнений, являющихся тождествами для всех х.
- •Примеры для самостоятельного решения. Решить системы уравнений
- •3.4 Однородные системы линейных уравнений
- •Найти все решения следующих однородных систем
- •Примеры для самостоятельного решения. Найти все решения следующих однородных систем
- •Ответы.
Примеры для самостоятельного решения.
32. Числа 204, 527, 255 делятся на 17. Не раскрывая определителя, доказать, что определитель
 делится на 17.
делится на 17.
33. Числа 121, 187, 253 делятся на 11. Не раскрывая определителя, доказать, что определитель
 делится на 11.
делится на 11.
В примерах 34-44 требуется, не раскрывая определителей, доказать справедливость равенств.
34.
 ,
35.
,
35.
 ,
,
36.
 ,
,
37.
 ,
,
38.
 ,
39.
,
39.
 ,
,
40.
 ,
41.
,
41.
 ,
,
42.
 ,
,
43.
![]() ,
,
44.

45. Упростить определитель
![]() ,
,
46. Имеется определитель
 ,
вычислить
,
вычислить
 .
.
47. Изменится ли определитель третьего порядка, если все его столбцы написать в обратном порядке?
48. С помощью разложения по элементам строки или столбца вычислить определители
а)
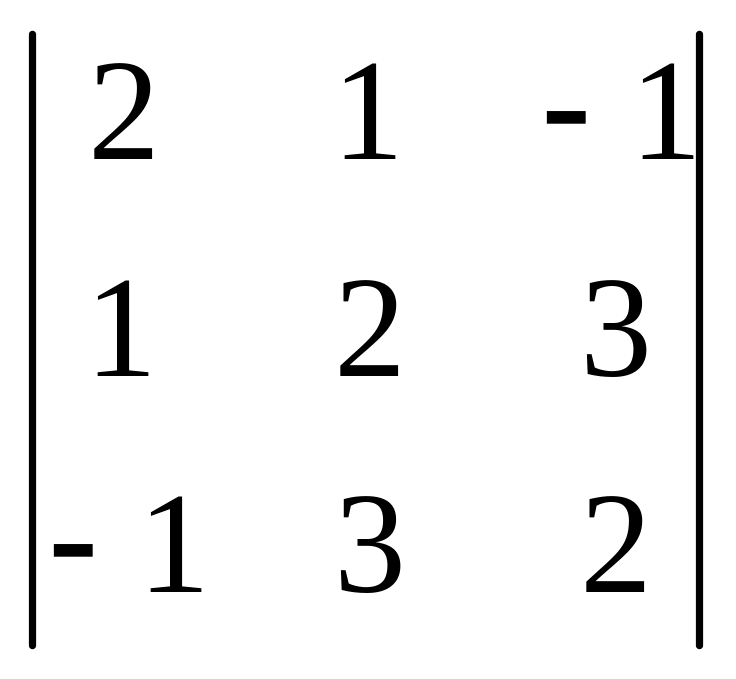 ,
б)
,
б)
 ,
в)
,
в)
 .
.
49.
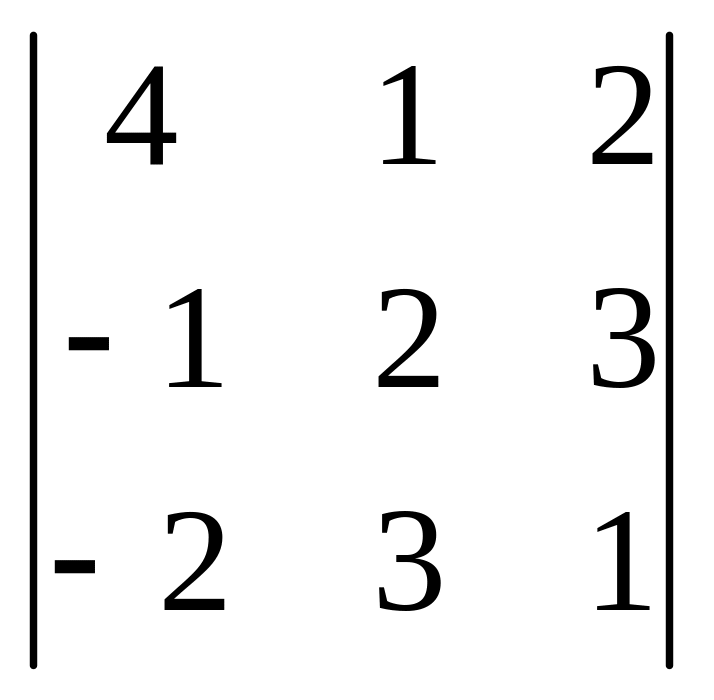 ,
50.
,
50.
 ,
51.
,
51.
 ,
,
52.
 ,
53.
,
53.
 ,
54.
,
54.
 .
.
55. Доказать справедливость равенства
 .
.
____________________________________________________________________
1.3. Определители высших порядков
Все перечисленные выше свойства определителей второго и третьего порядков переносятся на определители любого порядка. При вычислении определителей выше третьего порядка основную роль играют свойства 8 и 9. С помощью свойства 8 добиваются того, чтобы в некоторой выбранной строке стояли нули, кроме, может быть, одного. Затем, применяя свойство 9, разлагают определитель по этой строке и тем самым сводят его вычисление к нахождению определителя меньшего порядка. Повторяя этот прием, в конце концов получим определитель третьего или второго порядка. Разумеется, вместо строк можно выбрать столбцы, используя свойство их равноправности.
________________________________________________________________________________
Пример 56. Вычислить определитель
 ,
,
Решение. Используем свойство 8 для получения нулей в какой-нибудь строке. Проще получать нули в строке, имеющей единицу; например, выбираем первую строку. Умножим 1-й столбец на (-2) и прибавим ко второму

Из второго вынесем общий множитель 5. Применим процедуру получения нулей к 3-му и 4-му столбцам. Для этого 1-й столбец умножим на (-3) и прибавим к 3-му столбцу, затем 1-й столбец умножим на (-4) и прибавим к 4-му столбцу
 .
.
Разложим определитель по 1-ой строке, затем вынесем общий множитель из второй строки (-2) и из третьей строки (-1)
 .
.
Получим нули в 1-м столбце, для этого из 2-й и 3-й строки поочередно вычтем 1-ю строку

Разложим определитель по 1-му столбцу
![]()
Примеры для самостоятельного решения.
Вычислить определители:
57.
 , 58.
, 58.
 ,
,
59.
 , 60.
, 60.
 .
.
61. Изменится ли определитель четвертого порядка, если все его столбцы написать в обратном порядке?
2. Матрицы
2.1. Линейные действия с матрицами.
Совокупность чисел, расположенных в m строках и n столбцах называется матрицей m×n. Символически матрицу записывают так:
 ,
(i=1,2,3,…,m; j=1,2,3,…,n).
,
(i=1,2,3,…,m; j=1,2,3,…,n).
Первый индекс i у элемента aij означает номер строки; второй j – номер столбца, в котором стоит этот элемент.
Две матрицы A=(aij) и B=(bij) одной и той же размерности считаются равными, если все соответствующие их элементы равны, то есть aij=bij. Матрицы разной размерности не сравниваются между собой.
Квадратной матрицей порядка n называется матрица, у которой число строк равно числу столбцов n.
Квадратная матрица, у которой вне главной диагонали элементы равны нулю, называется диагональной матрицей. Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной.
 .
.
Линейными действиями над матрицами называется сложение матриц и умножение их на число.
Сложение матриц осуществляется поэлементно:
S = A+B= (aij)+ (bij) = (aij+ bij).
или

Умножение матрицы на число:
 .
.
Обратите
внимание на то, что все элементы матрицы
умножаются на число
![]() ,
а при умножении определителя на число
– умножаются на это число только элементы
одной строки ( или элементы одного
столбца ).
,
а при умножении определителя на число
– умножаются на это число только элементы
одной строки ( или элементы одного
столбца ).
Свойства сложения матриц и умножения на число
1) A+B = B+A; 2) (A+B)+C = A+(B+C);
3) λ(A+B) = λA+λB; 4) (λ+μ)A = λA+μA;
5) λ(μA) = (λμ)A.
Матрица 0, целиком, состоящая из нулей, называется нулевой. Для нее A+0=A.
Сложение матриц имеет обратное действие – вычитание, которое также осуществляется поэлементно:
С = A-B= (aij) – (bij) = (aij – bij).
Операция над матрицей A, при которой ее строки становятся столбцами с теми же номерами, а столбцы строками, называется транспонированием. Транспонированная матрица A обозначается AT. Например, если
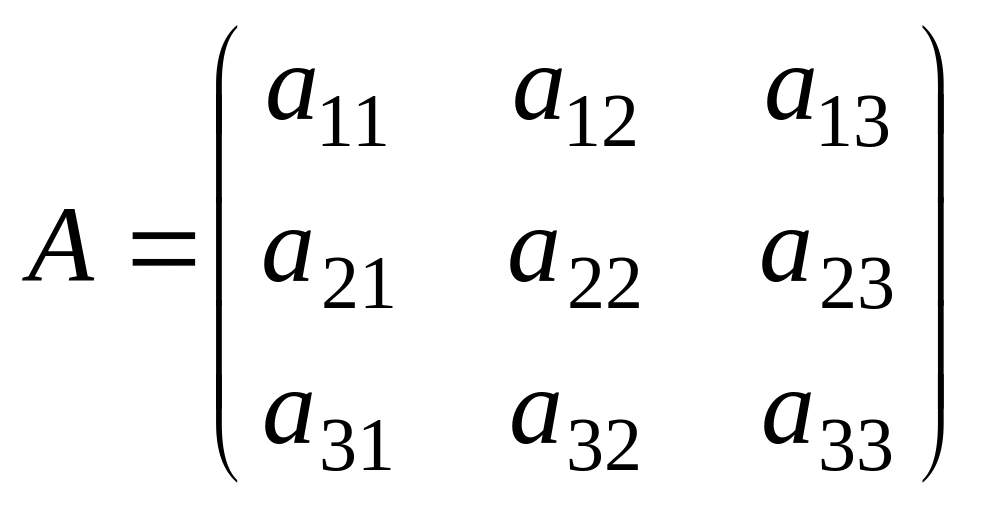 ,
то
,
то
 .
.
________________________________________________________________________________
Пример 62. Пусть
![]() .
Найти S =
A+B + AT+
BT.
.
Найти S =
A+B + AT+
BT.
Решение. Пользуясь свойствами сложения матриц, имеем
S = A+B + AT+ BT = (A+ AT)+(B+ BT).
Так как
![]() ,
поэтому
,
поэтому

Пример 63. Вычислить C=3A-2B, если
 .
.
Решение. Имеем
 ,
поэтому
,
поэтому
 .
.
