III. Поиск решения и составление плана решения задачи.

На этом этапе учащийся должен провести цепочку рассуждений (разбор задачи), которые приведут к составлению плана решения задачи.

Анализ может быть проведен учеником как самостоятельно, так и с помощью учителя. В последнем случае педагог проводит беседу, которая в методической литературе носит название «разбор зада­чи». В любом случае поиск решения облегчается, если опирается на модель задачи.

В начальной школе используются различные способы разбора текстовых задач:

1. от данных задачи к ее вопросу (синтетический способ);

2. от вопросов задачи к ее данным (аналитический способ);

3. комбинированный способ (аналитико-синтетический);

4. разбор по существу;

5. способ, основанный на аналогии.

Поскольку основными являются первые два способа, дадим характеристику каждому из них.

Разбор задачи от числовых данных состоит в том, что к двум числовым данным подбирается вопрос, затем к следующим двум данным, одно из которых может быть результатом первого действия, подбирается следующий вопрос. И этот процесс продолжается, пока не будет получен ответ на вопрос задачи. Суть данного способа, таким образом, заключается в вычлене­нии из составной задачи простых задач и их решении.

Второй вариант состоит в том, чтобы подобрать два числа, выражающих либо значение каких-либо величин, либо отношения меж­ду величинами, таким образом, чтобы дать ответ на вопрос задачи. Одно из чисел или оба могут оказаться неизвестными. Для их нахождения подбирают два других числа, и процесс продолжается до тех пор, пока не находят известные числовые данные. При данном способе также в конечном счете происходит вычленение простых задач из составной и их решение. Этот разбор заканчива­ется составлением плана решения.

Разница заключается только в том, что при синтетическом способе порядок вычленения простых задач из составных соот­ветствует плану решения, а при аналитическом — противоположен плану.

Учителя предпочитают разбор от данного к вопросу задачи как наиболее легкий и доступный для детей, что неверно. Каждый из этих способов имеет свои достоинства и недостатки. Например, при разборе задачи от данных к вопросу мы нередко сталкиваемся с неоднозначностью ответа на вопрос. Например, из того, что мас­тер обрабатывает за 6 ч 72 одинаковые детали, можно узнать:

1. сколько деталей мастер обрабатывает за 1 ч;

2. сколько времени он тратит на изготовление одной детали.

Рассуждение от вопроса к данным также не всегда эффективно. При решении задач в 3 действия и более не каждый ученик может удержать в памяти всю логическую цепочку. Если задача допускает разные способы решения, то уже в самом начале разбора ребенок сталкивается с вариативностью рассуждений.

Ни один из способов разбора не может считаться универсальным.

Продумывая работу над той или иной задачей, учитель должен творчески подходить к выбору способа разбора. Остано­вившись на одном из них, он должен позаботиться о четкости, точности вопросов, которые будут задаваться в ходе анализа. Хотя не может быть полного единообразия при разборе всех задач выб­ранным способом, нетрудно заметить некую общую структуру воп­росов для каждого способа разбора.

При аналитическом способе обычно задают вопросы:

1-го вида

1. Что достаточно знать, чтобы ответить на вопрос задачи?

2. Знаем... ?

3. Что нужно еще узнать?

2-го вида

1) Можем ли сразу узнать... ?

В случае отрицательного ответа на этот вопрос:

2. Почему? В случае положительного ответа:

3. Что нам для этого известно?

При синтетическом способе обычно задают вопросы:

1. Что спрашивается в задаче?

2. Берем любые два данных. Задаем вопрос: Зная ... и зная ..., что можно узнать?

3. Отвечаем на вопрос, выбираем ответ, приближающий к от­вету на вопрос задачи.

4. Далее пункты 2 и 3 повторяются до получения ответа на вопрос задачи.

Можно эту же памятку представить в виде обобщений графической схемы:

Разбор задачи

Зная

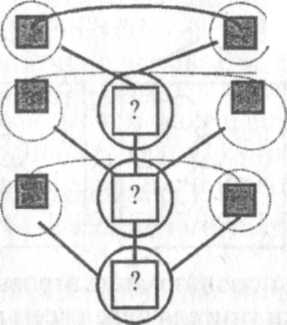
ч то можно узнать?

Способ разбора по существу предполагает осмысление основно­го отношения между величинами, данными или искомыми.

При обучении этому приему учащимся предлагается памятка:

1. Подумай, что обозначает каждое число в задаче.

2. Найди в задаче пары чисел, связанных между собой по смыслу; подумай, что можно узнать по этим данным, и составь из них выражения.

3. Из чисел задачи и полученных выражений попробуй соста­вить новые выражения и объясни их смысл.

4. Отбери те выражения, которые нужны для решения задачи

Одним из эффективных приемов поиска плана решения задачи, позволяющих организовать продуктивную мыслительную деятель­ность учащихся, является использование аналогии. Этот способ предполагает следующую цепочку рассуждений:

1. выявление полного или частичного сходства между значе­ниями величин и условий ранее решенной и вновь предложенной задачи;

2. выдвижение предположения о решении новой задачи с пол­ным или частичным использованием плана ранее решенной, похо­жей задачи.

В основе аналогии лежит сравнение. Поэтому для использова­ния этого приема необходимо сначала восстановить способ реше­ния предшествующей задачи. Затем предлагается новая (аналогич­ная) задача. Учащиеся выявляют сходство отношений в них и делают заключение о степени совпадения планов решения. Затем они составляют план решения новой задачи.