3. Проектирование кулачкового механизма

Задача проектирования кулачкового механизма состоит в построении профиля кулачка по заданным законам движения кулачка и толкателя (кинематический синтез) и динамическим условиям (минимальному углу передачи движения 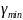). Углом передачи движения γ называется угол между направлениями абсолютной и относительной скоростей толкателя.

3.1. Графическое интегрирование по методу хорд

Закон движения ведомого звена кулачкового механизма задан графиком ускорения a=a(t) (рис. 7) или аналогом ускорений 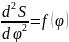. Для кулачка с качающимся толкателем задано 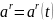или

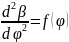
Для построения профиля кулачка нужно иметь закон изменения перемещения толкателя по времени, который можно найти, дважды графически интегрируя график a=a(t).

Порядок графического интегрирования:

1. В произвольном масштабе К_а и масштабе K_φ строим диаграмму ускорений толкателя.

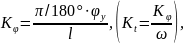
где φ_у – угол удаления в градусах;

ω – угловая скорость кулачка;

l – отрезок оси абсцисс, изображающий угол φ_у , в мм.

При построении диаграммы ускорений следует учитывать, что отношение ординат h´ и h´´, соответствующих максимальным значениям ускорений при удалении и возвращении, связано зависимостью

2. Углы φ_у и φ_в делим на равные части таким образом, чтобы момент времени, при котором a=0, совпадал с одним из делений. Если 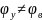, то промежутки времени 0-1, 1-2 … на участке удаления могут быть не равны промежуткам времени на участке возвращения.

3. В серединах промежутков 0-1, 1-2, 2-3 … проводим ординаты до пересечения с кривой графика и полученные точки сносим на ось ординат. Получаем ряд точек 1´, 2´, 3´ …

На участке 1-2, где кривая ускорений имеет экстремум, ордината 02´ должна быть подобрана такой, чтобы площадь прямоугольника с высотой 02´ и основанием 1-2 была равна площади фигуры с тем же основанием и ограниченной сверху кривой ускорений. То же относится и к участку 4-5.

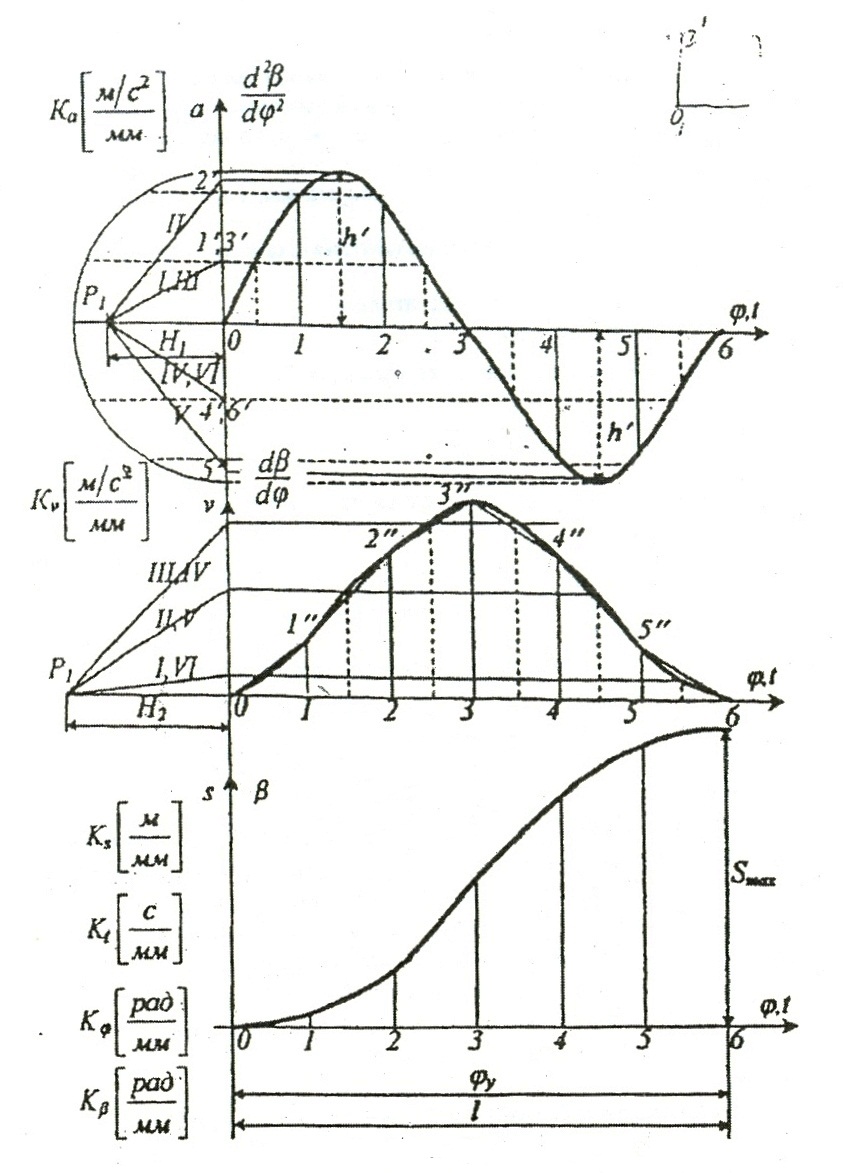
Рис. 7.

4. Соединяя произвольно взятую на продолжении оси t точку Р₁, принимаемую за полюс, с точками 1´, 2´, 3´ получаем лучи I, II, III …

5. На графике V=V(t) из т. О проводим в интервале 0-1 прямую 0-1'', параллельно лучу 1, в интервале 1-2 - прямую 1''-2'', параллельную лучу II и т.д. Полученная ломаная линия (в пределе кривая) представляет кривую изменения скорости по времени.

6. Аналогично интегрируя кривую V=V(t), получаем кривую перемещения S=S(t).

7. Определяем масштабы диаграмм, начиная с масштаба K_S.

– для кулачкового механизма с поступательно движущимся толкателем,

где h - ход толкателя, м;

S_max – максимальная ордината графика S=S(t).

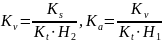
Для кулачкового механизма с качающимся толкателем определяют масштабы K_β и K_S

, ,

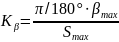где β_max – максимальный угол качания коромысла, в градусах;

l_AB – длина коромысла, м.

Примечание:

1. На рис. 7 показано построение синусоиды. Для этого слева от оси а проводится полуокружность диаметром 2h´, которая затем делится на 6 равных частей. Из точек деления проводятся прямые параллельные оси абсцисс до пересечения с соответствующими ординатами. Найденные таким образом точки принадлежат синусоиде. Аналогично следует строить косинусоиду.

2. На рис. 7 показано построение графиков движения только для участка удаления.