2. Производная сложной функции.
Пусть переменная у есть функция от переменной , т.е. а переменная в свою очередь есть функция от независимой переменной х, т.е. = (х). Тогда говорят, что задана сложная функция у = f((x)).
Теорема: Если y = f() и = (х) дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную самого промежуточного аргумента по независимой переменной х, т.е.
.
Правило
дифференцирования сложной функции
может быть записано и в других формах:
или
.
Используя формулы
для дифференцирования элементарных
функций и правило дифференцирования
сложной функции, можно составить ещё
одну таблицу производных с учетом
сложности функций. Пусть
,
тогда получаем:
Название функции |
Производная функции |
Степенная |
|
Показательная |
|
Логарифмическая |
|
Тригонометрические |
|
Обратные тригонометрические |
|
;
;
;
;
;
;
;
;
;
;
;
;
.
Пример 3. Найти производную функции:
1)
,
2)
,
3)
.
Решение: 1)
=
.
2)
=
=
.
3)
=
=
=
.
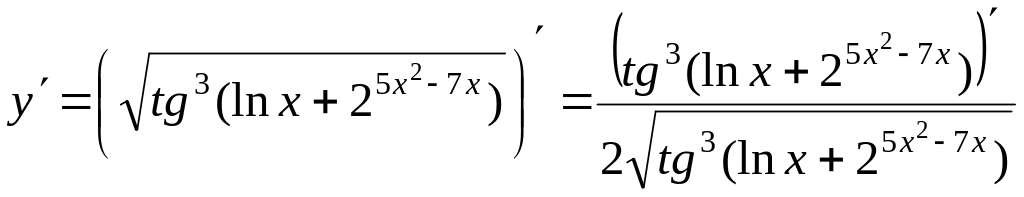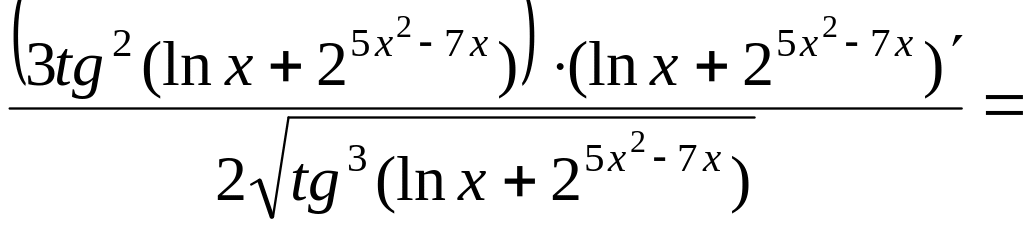
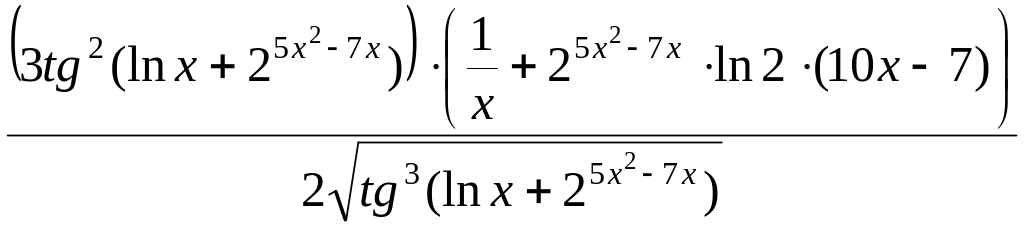Лекция 3. Логарифмическая производная. Производная неявной функции. Производные высших порядков.
1. Логарифмическая производная
При нахождении
производных от показательно-степенных
функций вида
,
а также других громоздких функций,
допускающих логарифмирование, удобно
применить логарифмическую
производную.
Определение:
Логарифмической производной от функции
y
= f(х)
называется производная от логарифма
этой функции:
.
Выведем формулу для вычисления производной
показательно-степенной функции
или
.
Прологарифмируем
обе части равенства, и воспользуемся
свойством логарифма
.
Получаем:
,
, 
.
Продифференцируем обе части равенства и используем правило дифференцирования произведения двух функций:
,
,
,
или окончательно получаем формулу
,
которую можно использовать для вычисления
производной показательно-степенной
функции вида
.
Пример 1.
Вычислить производные данных функций:
1)
,
2)
.
Решение: 1)
,
пусть
и
.
Тогда
и
.
Подставим эти выражения в полученную
формулу
.
Получаем
.
2)
,
пусть
и
,
тогда
и
.
Получаем
=
.
2. Производная неявной функции
Пусть функция y
= f(х),
имеющая производную в точке х0,
задана неявно уравнением F(x,y)
= 0. Тогда
можно найти, продифференцировав уравнение
F(x,y)
= 0 и выразить
.
Пример 2. Найти производные функций заданных неявно:
1)
,
2)
,
3)
.
Решение: 1)
,
дифференцируем обе части равенства,
считая х
переменной, а у
функцией, зависящей от х.
,
- из полученного равенства выразим
с помощью арифметических преобразований:
,
или
.
2)
,
,
,
,
,
,
.
3)
,
,
,
,
,
,
.