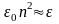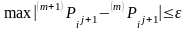- •1. Численные модели для прогнозирования показателей разработки газовых месторождений при газовом режиме
- •1.1. Разностные представления дифференциальных операторов.
- •Или пренебрегая величинами , имеем для
- •1.2.Уравнения типа уравнения теплопроводности и фильтрации.
- •1.2.1. Рассмотрим представление в конечно – разностной форме одномерного (一维)дифференциального уравнения параболического(抛物线)типа
- •1.3. Прогонка.
- •1.4. Потоковая прогонка.
- •1.5. Двумерная задача фильтрации однофазных систем.
- •1.5.0 Общие сведения.
1.3. Прогонка.
1.3.1. С начала 50-х годов для решения задач нестационарной фильтрации газов все более широкое применение находят численные методы решения с использованием ЭВМ. Первоначально исследовались одномерные задачи фильтрации идеального газа. Были получены практически точные решения, позволившие оценить точность приближенных методов и обосновать справедливость применения упрощенных методов определения показательной разработки месторождений природных газов.
В дальнейшем были получены решения для нестационарной фильтрации реального газа, совместного течения газа и конденсата, газированной нефти, вытеснения газа и нефти водой и т.п.
В настоящее время все большое значение приобретает решение двумерных и многомерных уравнений фильтрации, которые позволяют учесть более точно реальные условия разработки газовых месторождений.
В настоящем разделе мы рассмотрим способ решения одномерного уравнения фильтрации газа. Метод этот называется методом прогонки [22]. Он является наиболее эффективным для решения систем трехдиагональных линейных уравнений, к которым сводится численное решение дифференциального уравнения.
Это по существу специальный метод исключения Гаусса. Идея заключается в замене разностного уравнения второго порядка тремя разностными уравнениями первого порядка.
1.3.2. Рассмотрим применение метода прогонки на примере уравнения фильтрации газа в круговом пласте. Мы не будем ограничиваться идеальным газом или постоянной мощностью пласта, а запишем уравнение в самом общем виде:
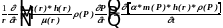 (1.3.1)
(1.3.1)
Начальные и граничные условия:
t= 0 P= Pk = const (1.3.2)
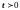 r= R0
r= R0
 (1.3.3a)
(1.3.3a)
r=
R k
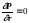 (1.3.3б)
(1.3.3б)
Далее пусть уравнение состояния для газа имеет вид:
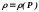 ,
(1.3.4a)
,
(1.3.4a)
Если газ идеальный, то имеем
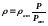 ,
,
если газ реальный, то имеем
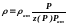 ,
,
для упругого пласта имеем
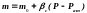 (1.3.4б)
(1.3.4б)
Для получения универсального решения справедливого для любых рассматриваемых параметров представим дифференциальное уравнение и граничные условия в безразмерном виде, для чего введем безразмерные параметры и переменные:
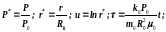
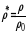 ;
;
|
(1.3.5) |
С учетом (1.3.5) уравнение (1.3.1) и граничные условия (1.3.2) и (1.3.3) имеют вид (для простоты в дальнейшем звездочки будем опускать.)
|
(1.3.1’) |
|
(1.3.2’) |
|
(1.3.3’a) |
|
(1.3.3’б) |
Уравнение (1.3.1) является общим нелинейным параболическим дифференциальным
уравнением. Из него легко получить,
например, дифференциальные уравнения
для течения идеального газа. Для этого
надо положить
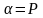 ,
а
,
а
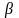 =1.
=1.
1.3.3. Представим теперь задачу (1.3.1’)-(1.3.3’б) в конечно-разностной форме.
При этом рассмотрим пространственно-временную непрерывную область в виде сеточной области.
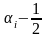 ;
;
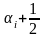
-
J

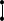 +1
J
+1
Jj-1
Будем использовать
неявную разностную схему вида крест.
Граница пласта и скважина расположены
в середине интервалов,
чтобы получить
0 1 2 I-1 I I+1 m-1 m
Рис.1.1
лучшую аппроксимацию,
порядка
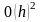
|
(1.3.6)
|
|
(1.3.7) |
Для записи разностной схемы уравнения
(1.3.1’) поступим следующим образом.
Обозначим
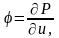 тогда левая часть уравнения (1.3.1’)
записывается в виде
тогда левая часть уравнения (1.3.1’)
записывается в виде
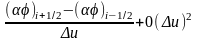 и далее, заменяя
и далее, заменяя
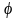 на разности
на разности
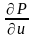 ,
получим
,
получим
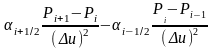
Правую часть (1.3.1’)
представим согласно мнемонической
схемы на рис.1.1 и, учитывая, что
пространственные разности берутся на
верхнем временном слое, имеем после
некоторых преобразований
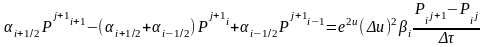
Или окончательно
|
(1.3.8)
|
|
(i=1, …n-1) |
|
|
Уравнение (1.3.8) совместно с (1.3.6) и
(1.3.7) представляют систему (n+1)
уравнения с (n+1) неизвестным.
При этом если коэффициенты при неизвестных
будут постоянными (а это на каждом
временном слое или итерации можно
получить, определяя коэффициенты
 и
и
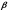 с предыдущего слоя или итерации), то
система линейна и имеет три диагонали.
с предыдущего слоя или итерации), то
система линейна и имеет три диагонали.
1.3.3.1.Перепишем в общем случае задачу (1.3.8), (1.3.6), (1.3.7) так
|
(1.3.9) |
|
(1.3.10) |
- общий вид граничных условий.
Пусть имеет место рекуррентное соотношение:
|
(1.3.11) |
Подставим в (1.3.9) выражение
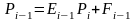 ,
тогда
,
тогда
|
(1.3.12) |
Сопоставляя (1.3.11) и (1.3.12), видим, что они
совпадают при любых значениях
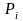 ,
если:
,
если:
|
(1.3.13) |
Если коэффициенты в точке
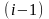 известны, то при помощи формул (1.3.13)
можно просчитать коэффициенты
известны, то при помощи формул (1.3.13)
можно просчитать коэффициенты
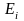 ,
,
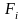 и т. д.
и т. д.
Затем, зная значения
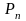 по формуле (1.3.11), можно определить
значения
для всех
по формуле (1.3.11), можно определить
значения
для всех
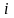 .
.
Для определения начальных значений
коэффициентов
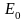 и
и
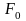 воспользуемся условиями (1.3.10).
воспользуемся условиями (1.3.10).
Тогда будем иметь
|
(1.3.14) |
В нашем конкретном случае имеем (см.1.3.6.)
|
|
Итак, для функций Ei и Fi имеем формулы прямой прогонки (1.3.13), (1.3.14)
Если En-1 и Fn-1 известны, то из граничного условия Pn = 2 P n-1+µ2
и P n-1=En-1 P n-1+ F n-1 можно получить значение Pn на границе. Т.е.
|
( 1.3.15)
|
В нашем случае с учётом (1.3.7) имеем
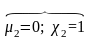
Итак, формулы (1.3.11) и (1.3.15) позволяют определить значения Pi для всех значений
i= n, n-1…0. (Это формулы обратной прогонки.)
1.3.3.2. Устойчивость метода прогонки.
Формулы прогонки (1.3.13), (1.3.14) и (1.3.15), (1.3.11) были нами получены формально. Мы делили на выражения (bi-ci Ei-1) и (1- 2En-1), предполагая, что они не равны нулю. Сейчас мы укажем достаточные условия, когда это можно делать.
Пусть
|
(1.3.16) |
Для устойчивости метода прогонки
достаточно иметь
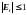 для всех i=1,2,..n-1
для всех i=1,2,..n-1
Это действительно так.
Рассмотрим разность
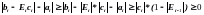 ,
при
.
,
при
.
Поскольку
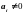 ,
то
,
то
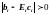 ,
т.е.
,
т.е.
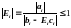 .
.
Отсюда, видно, что
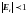 ,
если
,
если
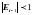 .
Тогда все
при
.
Тогда все
при
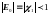 .
.
Рассмотрим теперь неравенство
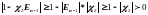 ,
т.к. или
,
т.к. или
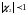 ,
или
,
или
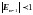 ,
,
т.е.
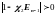
Таким образом, при выполнении условий (1.3.16) разностная задача, решаемая методом прогонки, имеет единственное решение.
1.3.4. В силу того, что решение
ведется на ЭВМ приближенно, с конечным
числом значащих цифр, возникают ошибки
округления. Из-за них фактически
находится не функция
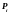 -
решение задачи (1.3.9), (1.3.10), а
-
решение задачи (1.3.9), (1.3.10), а
 -
решение той же задачи с возмущенными
коэффициентами
-
решение той же задачи с возмущенными
коэффициентами
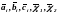 и
правыми частями
и
правыми частями
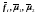 .
При этом, если процесс вычислений
происходит с возрастанием ошибки
округления, то это может привести как
к потере точности, так и к невозможности
продолжить вычисления из-за роста
получаемых величин.
.
При этом, если процесс вычислений
происходит с возрастанием ошибки
округления, то это может привести как
к потере точности, так и к невозможности
продолжить вычисления из-за роста
получаемых величин.
Например,
будем определять какую-либо величину
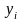 по формуле
по формуле
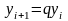 при
при
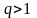 ,
тогда
,
тогда
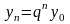 и для любого
и для любого
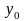 можно получить такую величину n
, при которой
можно получить такую величину n
, при которой
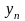 -
будет машинной бесконечностью. В этом
случае, в силу ошибок округления,
определяется не
-
будет машинной бесконечностью. В этом
случае, в силу ошибок округления,
определяется не
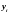 ,
а
,
а
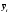 из уравнения
из уравнения
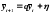 ,
где
,
где
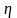 - ошибка округления.
- ошибка округления.
Для погрешности имеем уравнение
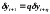 ,
,
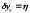
или
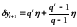 ,
,
откуда
видно, что ошибка
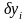 при
экспоненциально возрастает с ростом
i.
при
экспоненциально возрастает с ростом
i.
Для
метода прогонки, в силу условия
,
ошибка
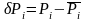 при определении
не нарастает.
при определении
не нарастает.
Действительно,
из уравнений
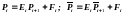
следует
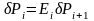 ,
,
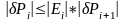 , т.е.
, т.е.
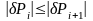 , т.к.
, т.к.
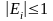
Отсюда и следует устойчивость метода прогонки.
Замечание. Если учесть, что в ходе вычислений возмущающимися являются и коэффициенты и , то показывается, что ошибка в определении в задаче (1.3.9),(1.3.10) пропорциональна квадрату числа узлов
|
|
где
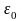 -
ошибка округления.
-
ошибка округления.
Отсюда видно, что существует связь между
точностью
определения
решения задачи, числом
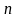 уравнений и числом значащих цифр ЭВМ,
так как
уравнений и числом значащих цифр ЭВМ,
так как
|
|
(Если разрядность машины 12 значащих
цифр -
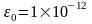 ,
n= 100, тогда точность
решения
,
n= 100, тогда точность
решения
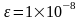 )
)
1.3.5. Выше уже отмечалось, что уравнение (1.3.8) описывает нелинейную фильтрацию газа в круговом пласте. Для решения задачи численным методом необходимо линеаризовать нелинейные коэффициенты. Этого можно достичь с использованием их значений, вычисленных при значении давлений на предыдущем временном слое, или для более точного учета их необходимо итерировать на каждом временном слое. Первым приближением служат нелинейные коэффициенты, вычисленные по данным решения на j-ом временном слое. Затем определяется приближенное решение на (j+1)-ом временном слое. Во втором приближении для вычисления нелинейных членов используется решение на (j+1)-ом слое. Вновь определяется решение на (j+1)-ом временном слое и т. д., до тех пор, пока не будет выполнено неравенство
|
|
Очевидно, что, начиная счет в обратном
порядке, получаем левую прогонку.
В этом легко убедиться самостоятельно.
Если у нас имеется какой-либо внутренний
узел
 ,
то можно получить метод встречных
прогонок, комбинируя правую и левую
прогонки. Отметим, что все эти прогонки
являются устойчивыми. ( См. Самарский
А. А. ‘’Теория разностных схем’’.
Наука, 1972 [26]).
,
то можно получить метод встречных
прогонок, комбинируя правую и левую
прогонки. Отметим, что все эти прогонки
являются устойчивыми. ( См. Самарский
А. А. ‘’Теория разностных схем’’.
Наука, 1972 [26]).

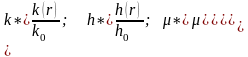
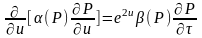
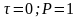
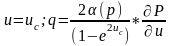
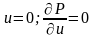
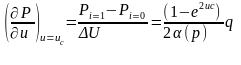
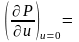
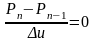
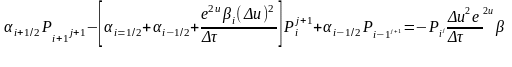
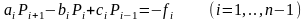
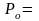
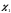
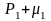 ;
;
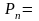
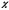
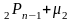
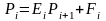 ,
,
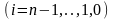
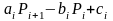
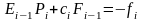
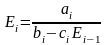 ;
;
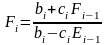
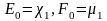
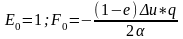

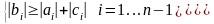
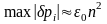 ,
,