Контрольная работа №2 в заданиях 51 – 60 найти неопределенные интегралы:
51.
а)
;
б)
;
в)
.
52.
а)
;
б)
;
в)
.
53.
а)
;
б)
;
в)
.
54.
а)
;
б)
;
в)
.
55.
а)
;
б)
;
в)
.
56.
а)
;
б)
;
в)
.
57.
а)
;
б)
;
в)
.
58.
а)
;
б)
;
в)
.
59.
а)
;
б)
;
в)
.
60.
а)
;
б)
;
в)
.
В заданиях 61 – 70 вычислить по формуле Ньютона-Лейбница определенные интегралы:
61.
.
62.
.
63.
.
64.
.
65.
.
66.
.
67.
.
68.
.
69.
.
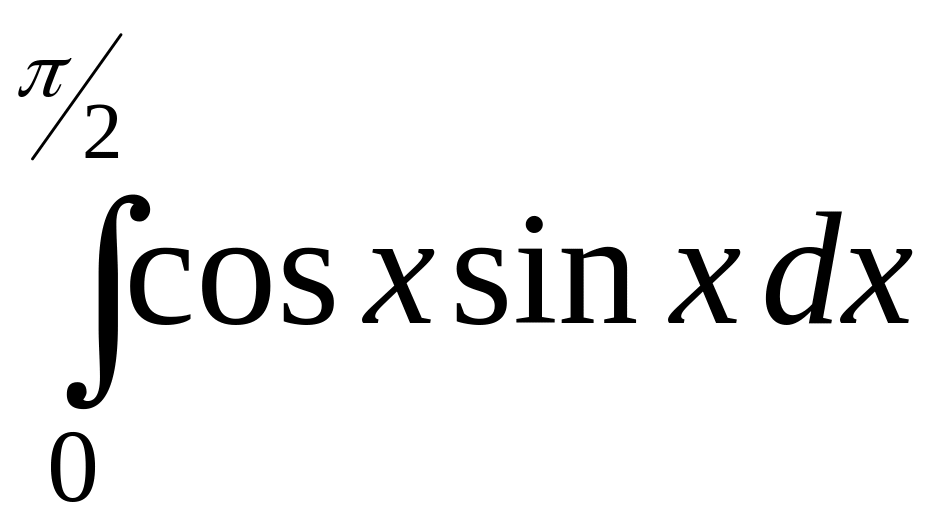70.
.
В заданиях 71 – 80 найти площадь фигуры, ограниченной указанными линиями. Сделать чертеж.
71.
у
= х4,
у2
= х.
72.
у
=
,
х
+ у
= 5.
73. у = – х2 – х + 6, 3х + у = 6. 74. у = 3 – х2, у = х2 + 1.
75. у = х3, у = 2 – х, у = 0. 76. у = –х2, х + у – 2 = 0.
77. у2 = 4х3, у = 2х2. 78. y = sinx, y = cosx, x = 0.
79.
у
=
,
у
= 6 – х.
80.
у
=
,
у =
4 – х.
В
задачах 81 – 90 ненагруженная пружина
имеет длину
(м).
Сила F
(Н)
растягивает пружину на расстояние х
(м).
Какую работу надо совершить, чтобы
растянуть пружину от
(м)
до
(м):
81.
,
,
,
,
.
82.
,
,
,
,
.
83.
,
,
,
,
84.
,
,
,
,
.
85.
,
,
,
,
.
86.
,
,
,
,
.
87.
,
,
,
,
.
88.
,
,
,
,
.
89.
,
,
,
,
.
90.
,
,
,
,
.