Тема 5. Определенный интеграл

Литература

1.Демидович Б.П., Кудрявцев В.А., Краткий курс высшей математики. М. Астрель-АСТ. 2001. Гл. ХIV, XV.

2. Баврин И.И., Матросов В.Л. Высшая математика. М. Владос. 2002. Гл. 6.

3. Письменный Д.Т. Конспект лекций по высшей математике. М. Айрис Пресс. 2000. Ч. 1. Гл. VIII.

Примеры решения задач.

Задача 23. Вычислить определенный интеграл

.

Решение. Данный интеграл приводится к табличному с помощью подстановки t = lnx. Отсюда . Определим пределы интегрирования новой переменной. При х = 1, t = ln1 = 0, при х = е, t = lne = 1. Произведем замену переменной и используем формулу Ньютона–Лейбница.

= = = arcsin1 – arcsin0 = .

Задача 24. Вычислить определенный интеграл .

Решение. Преобразуем подынтегральную функцию

= = = .

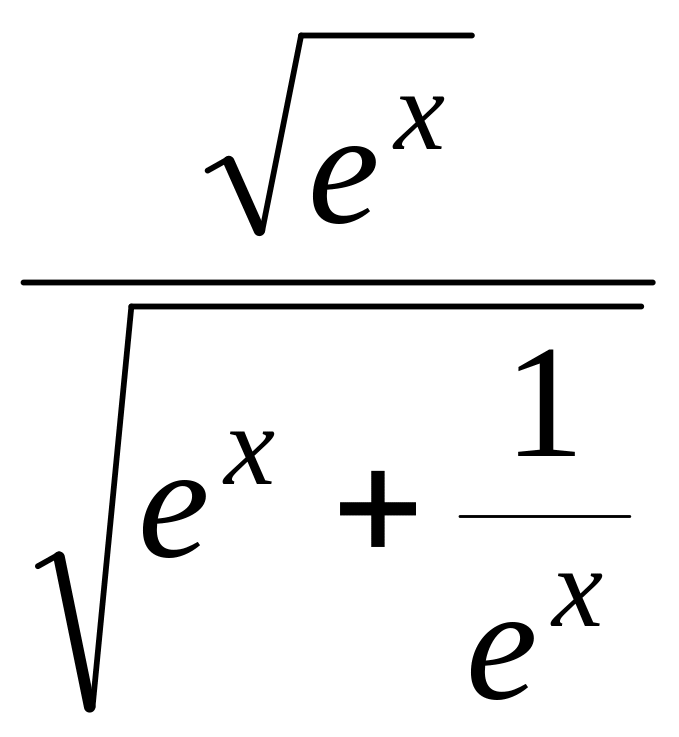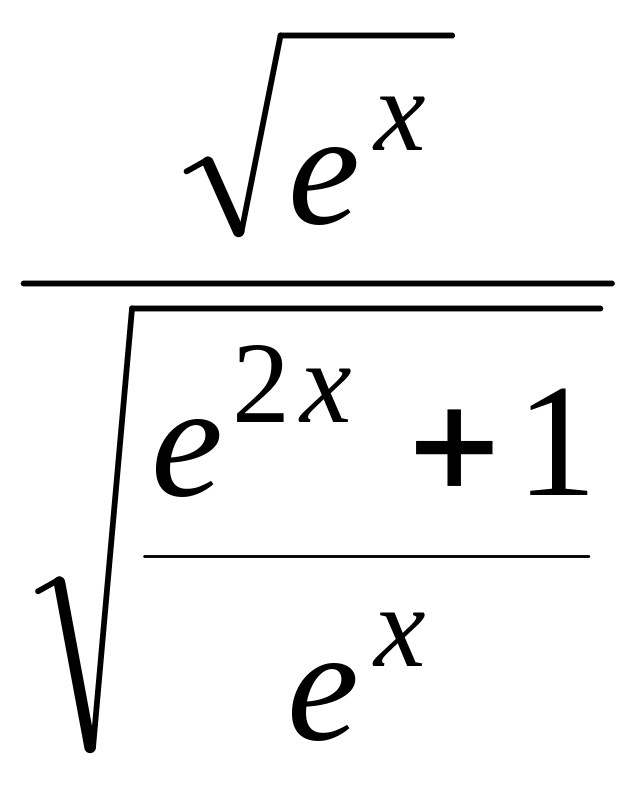Обозначим t = e^x, тогда dt = e^x dx. Определим пределы интегрирования новой переменной. При х = 0, t = e⁰ = 1, при х = 1, t = e¹ = e. Тогда

= = = =

= = .

Задача 25. Вычислить определенный интеграл .

Решение. Применим формулу интегрирования по частям для определенного интеграла

.

Положим u = ln(x² +4), dv = dx, тогда , v = x. Имеем

= = =

= = =

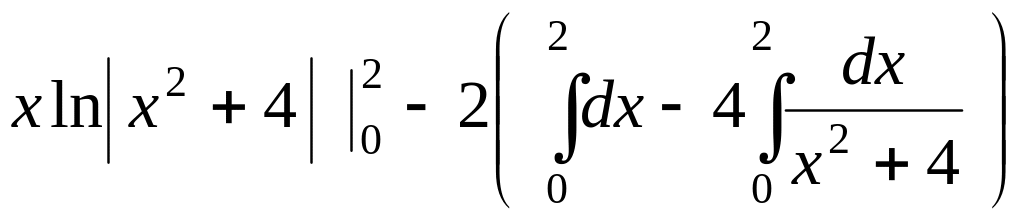= 2 ln(4 + 4) – 0 – 2 (2 – 0 – 2arctg1 + 2 arctg0) =

= 2 ln8 – 2(2 – 2 + 20) = 2 ln2³ – 4 +  = 6 ln2 – 4 + .

Задача 26. Найти площадь фигуры, ограниченной линиями:

y = x², , y = 0, x = 2 (x > 0).

Решение. Данную фигуру можно разбить на две криволинейные трапеции, площади которых соответственно равны: S₁ и S₂. (Рис. 9).

Тогда S = S₁ + S₂. Найдем абсциссу точки А –точки пересечения двух линий.

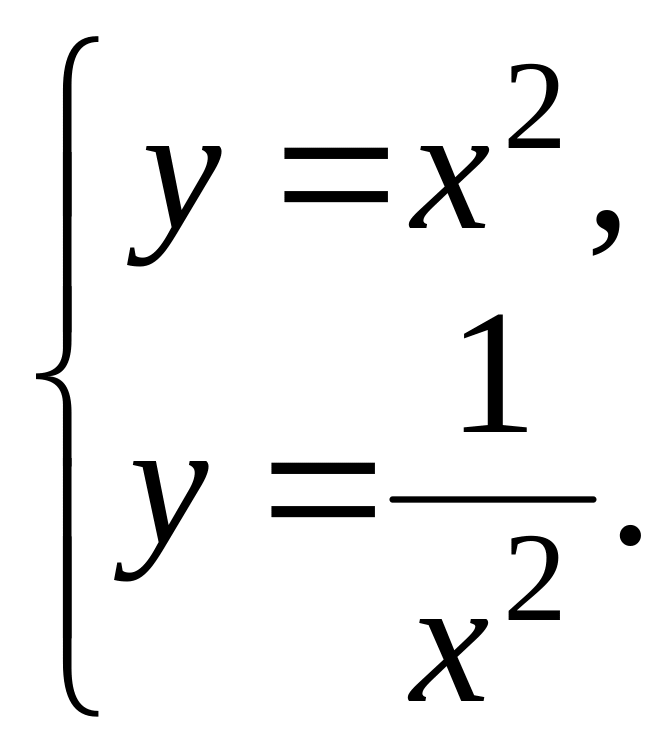
Отсюда , или х⁴ = 1, то есть х₁ = –1 и х₂ = 1. Так как по условию x > 0, то абсцисса точки А равна 1.

у

2,0

1,5

1,0

0,5 у = 1/х

0 0,5 1,0 1,5 2,0 2,5 х

Рис. 9.

Следовательно,

= , и тогда

( кв.ед.).

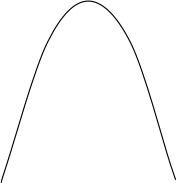
Задача 27. Найти площадь фигуры, ограниченной параболой

и прямой y = x + 2.

Решение. 1. Изобразим данные линии на чертеже и заштрихуем фигуру, площадь которой нужно найти. Графиком функции является парабола. Найдем производную данной функции и, приравняв ее к нулю, определим критическую точку.

.

Пусть y′ = 2 – х = 0. Отсюда х = 2. Это – абсцисса вершины параболы. Ордината вершины . Ветви параболы направлены вниз. Найдем точки пересечения параболы с осью Ох, положив у = 0. Тогда или . Решив данное квадратное уравнение, получим х₁ = -2 и х₂ = 6. Строим параболу (рис. 10).

у

8

у = х + 2

6

4

2

–2 0 2 4 6 х

Рис. 10.

2. Графиком функции у = х + 2 является прямая, для ее построения достаточно двух точек. При х = 0, у = 2, при х = 2, у = 4. Строим прямую.

3. Площадь фигуры, ограниченной сверху непрерывной кривой , снизу – непрерывной кривой находится по формуле:

,

где a и b – абсциссы точек пересечения кривых.

Для нахождения точек пересечения данных линий, решим систему уравнений:

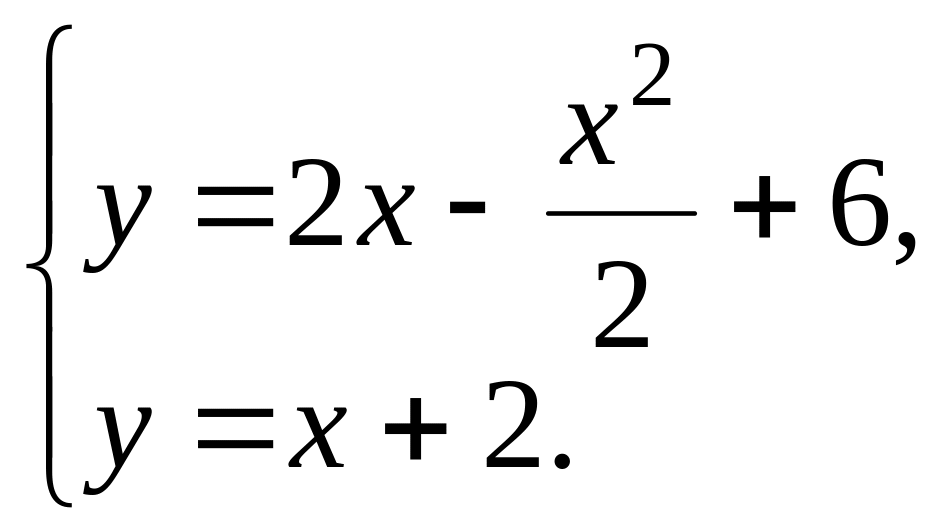
, или .

Решая полученное квадратное уравнение, получим х₁ = –2 и х₂ = 4, следовательно, а = –2; b = 4. Применяя формулу площади, составим интеграл

.

Итак, искомая площадь S = 18 (кв. ед.).

Задача 28. Найти площадь фигуры, ограниченной кардиоидой

r = a (1 – cos).

Решение. Для вычисления площади фигуры, ограниченной кривой, заданной в полярных координатах r = r(), ( <  < ), используем формулу

.

Тогда искомая площадь будет равна

= =

=

=

= =

=

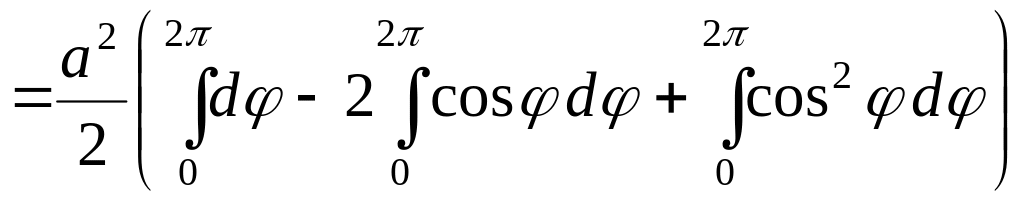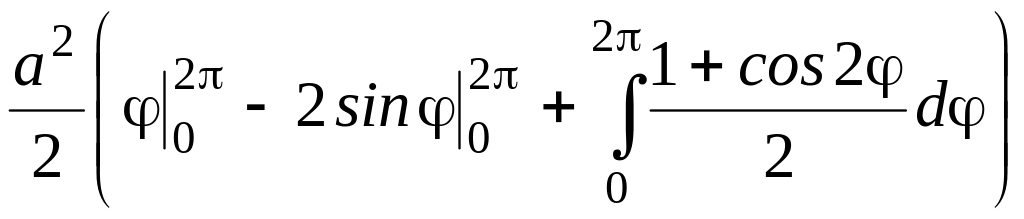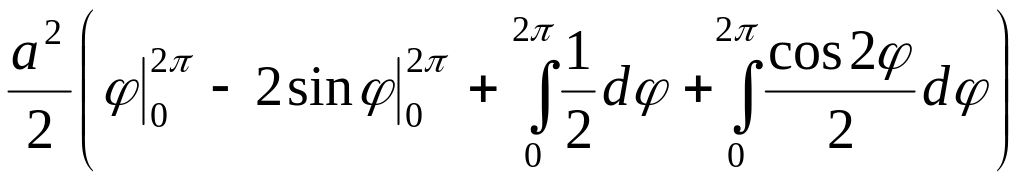= = (кв. ед.).

Задача 29. Деформация винтовой пружины пропорционально приложенной силе F. Какую работу нужно совершить, чтобы сжать пружину на 5 см, если сила 200 Н сжимает эту пружину на 1 см?

Решение. Работа, произведенная переменной силой при перемещении точки ее приложения по оси Ох от до находится по формуле

,

где , , – длина пружины в ненагруженном состоянии.

В нашем случае , , так как , , имея ввиду, что расстояние в системе СИ измеряется в метрах.

Для силы, пропорциональной величине деформации х, , где – жесткость деформируемого тела, х – величина деформации. По условию задачи, при х = 1 см, сила . Отсюда

.

Тогда работа, которую нужно совершить, чтобы сжать пружину на 5 см будет равна

.