Построение доверительного интервала для средних удельных затрат

Найдем теперь все гипотезы о средних удельных затратах a₁, которые не противоречат найденному коэффициенту регрессии b₁=26,312. Сформулируем две гипотезы:

нулевая гипотеза H₀: a₁=а,

альтернативная гипотеза H₁: a₁а.

Из правила принятия гипотез следует, что коэффициент регрессии b₁=26,312 не противоречит гипотезе H₀ , если выполняется неравенство

или . (4.9)

Множество всех значений а, удовлетворяющих неравенству (4.9), образует доверительный интервал

(b₁ -, b₁ +).

Величина

называется предельной ошибкой. Для рассматриваемой задачи предельная ошибка будет равна

=2,3066,427=14,821.

Тогда доверительный интервал имеет

нижнюю границу, равную 26,312-14,821=11,491,

и

верхнюю границу, равную 26,312+14,821=41,133,

Таким образом, с надежностью 95 % можно утверждать, что средние удельные затраты составят не менее 11,491 у.е. и не более 41,133 у.е.

Проверка общего качества уравнения регрессии

Мерой общего качества уравнения регрессии (соответствия уравнения регрессии статистическим данным) является коэффициент детерминации . При парной линейной регрессии коэффициент равен квадрату парного линейного коэффициента корреляции

.

Коэффициент детерминации характеризует долю общего разброса значений зависимой переменной , объясненного уравнением регрессии. Считается, что чем больше эта доля, тем лучше уравнение регрессии описывает исследуемую зависимость. В общем случае .

Существует несколько видов формулы линейного коэффициента корреляции, приведем основные из них:

,

где общая дисперсия результативного признака .

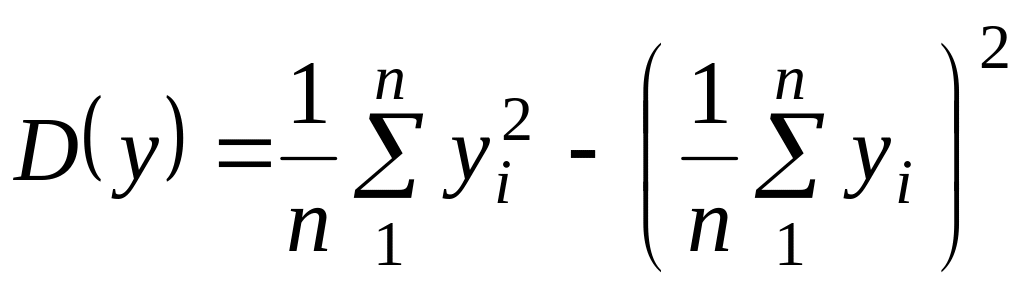Для расчета коэффициента детерминации определим значение линейного парного коэффициента корреляции через коэффициент регрессии:

.

Тогда коэффициент детерминации будет равен: Следовательно, 0,1% вариации затрат на реализацию объясняется изменчивостью объема продаж, т. е. уравнением линейной регрессии.

Прогнозирование

Уравнение регрессии

y^пр(x)= 142,16+26,312x

можно использовать для прогноза фактических затрат y. Найдем прогноз затрат при объеме продаж x₀ = 6,5. Подставляя значение x₀ в уравнение регрессии, получим

y^пр(6,5)= 142,16+26,3126,5=313,188 у.е.,

т. е. можно утверждать, что затраты на реализацию 6,5 ед. продукции составят 313,188 у.е. Используя это значение, построим доверительный интервал, в котором будут содержаться фактические затраты на реализацию объема продаж x₀=6,5. Для этого зададим доверительную вероятность =0,95 (=1-) и найдем предельную ошибку доверительного интервала m по формуле

m= =

141,945.

Здесь обозначает среднее арифметическое значений x_i.. Тогда доверительный интервал имеет:

нижнюю границу, равную y^пр(x₀)-m=313,188-141,945=171,243,

верхнюю границу, равную y^пр(x₀)+m= 313,188+141,945=455,133.

Доверительный интервал означает: с надежностью 95 % можно утверждать, что при объеме продаж x₀=6,5 ед. фактические затраты будут в интервале (171,243, 455,133), т. е. затраты составят не менее 171,243 у.е и не более 455,133 у.е.