Производящие функции для перестановок.

1. Воспользуемся связью

Тогда производящая функция для перестановок имеет вид:

Числа перестановки появляются в форме коэффициентов при

Воспользуемся производящими функциями для подтверждения ранее полученных результатов.

Перестановки с повторениями.

n элементов

n₁ n₂ n_l

В этом случае производящая функция имеет вид:

число перестановок из n элементов (выборка n=r)

А если надо найти число перестановок из r элементов? (r<n)

Тогда надо найти коэффициенты при и т.д.

2. Рассмотрим r перестановок из n различных элементов с неограниченными повторениями.

(известное соотношение)

(известное соотношение)

искомое число перестановок

Производящие функции, возникающие при изучении перестановок называют экспоненциальной производящей функцией, т.к.

Размещение и занятость.

«Размещение» – распределение объектов по ячейкам.

Объекты могут быть любой природы и в любом количестве.

Ячейки – независимо классифицируются по виду, вместимости, числу.

Порядок объектов, вкладываемых в ячейку может учитываться.

Задача о числе возможных способов размещений объектов в заданных ячейках называется задача о размещении.

(Задача о размещении – задача о разбиении элементов на множество классов).

Задача занятости исследует вопрос о числе объектов в заданных или произвольно выбранных ячейках.

Рассмотрим простейших случай:

n различных объектов

m различных ячеек.

Спецификация 1 – на занятость каждой ячейки не положено никаких ограничений.

Проанализируем ситуацию.

а). Первый объект размещается m способами.

б). Второй – m (ничего не изменилось)

…

объектов

……………………………………….

В

ячеек

результате по правилу умножения имеем способов.

Дано:

2 объекта, 3 ячейки.

1-я 2-я 3-я

1)	-	1	2
2)	1	2	-
3)	-	2	1
Всего 32 = 9 способов . 4)	2	1	-
5)	1	-	2
6)	2	-	1
7)	12	-	-
8)	-	12	-
9)	-	-	12

Подойдем к этому результату другим путем.

- индикатор занятости i-ой ячейки.

- попадание элементов в i-ю ячейку.

Распределение единственного объекта по ячейкам примем выражение

Индикатор распределения n различных объектов

Экспоненциальная производящая функция для последнего случая

Это производящая функция.

После раскрытия

возникают (перечисляются) комбинации вида

Энемератором занятости i-ой ячейки является

Конкретное число комбинаций получим, положив

Это соответствует ранее полученным результатам: размещения n объектов по m ячейкам.

II. Рассмотрим число способов размещения n различных элементов по m различным ячейкам при условии, что ни одна ячейка не оказывается пустой.

{

1

2

m

1} {1} {1}

-ячеек

………….

1

2

n

-объектов

вид энумератора

Энумератор имеет вид

Пусть , тогда ,

n – число объектов

m – число ячеек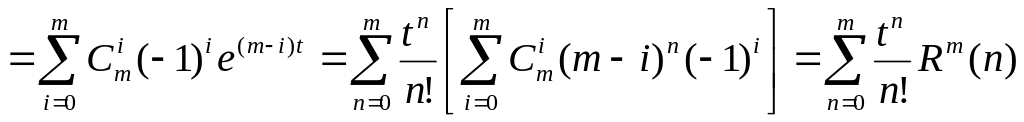

Число способов размещения n различных объектов по m различным ячейкам (ни одна ячейка не пустая!)

III. Найдем число способов размещения n различных элементов по m ячейкам при условии, что в i-ой ячейке (i=1,2,…m) помещается элементов

{

1

2

m

} { } { }

-ячеек

n объектов

………….

Индикатор ситуации

…

есть формула представления полинома

С уммирование идет по различным числам …

Искомое число

См. формулу перестановок n элементов, из которых принадлежит 1-му классу, - второму, и т.д.

Заключение:

Существует тесная связь размещений с сочетаниями и перестановками (результаты получились аналогичные).

Изучение размещений отличается своей спецификой и потому оправдывает самостоятельное рассмотрение.