МосГУ Зимняя экзаменационная сессия 2012-2013 учебного года Кафедра информатики и математики

Д исциплина Теория вероятностей и математическая статистика Факультет Экономики и управления Курс 2 дневное отделение

Экзаменационный билет № 0

1. Полная группа несовместных событий и формула полной вероятности.

2. Дисперсия дискретной случайной величины. Основные свойства дисперсии. Стандартное (среднее квадратическое) отклонение.

3. Решите задачу: В первой урне 4 черных и 16 белых шаров. Во второй урне 12 белых и 8 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна …

4. Решите задачу: Выборочное уравнение прямой линии регрессии Y на X имеет вид y=2,7+0,6x, а выборочные стандартные отклонения равны: _X=0,7, _Y=2,8. Тогда выборочный коэффициент корреляции  равен …

Утверждено на заседании кафедры информатики 08.04.2013 з аведующий кафедрой а.Ю.Выжигин

МосГУ Зимняя экзаменационная сессия 2012-2013 учебного года Кафедра информатики и математики

Д исциплина Теория вероятностей и математическая статистика Факультет Экономики и управления Курс 2 дневное отделение

Экзаменационный билет № 1

1. Классическое определение вероятности.

2. Нормальный закон распределения (закон Гаусса). Параметры нормального закона распределения.

3. Решите задачу: Двумерная дискретная случайная величина  задана законом распределения вероятностей: 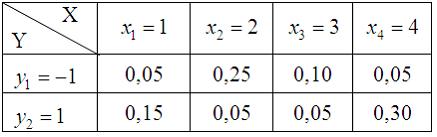Тогда вероятность 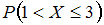 равна …

4. Решите задачу:

Дан доверительный интервал (20,1; 21,7) для оценки математического ожидания нормально распределенной случайной величины. Тогда точность этой оценки равна …

Утверждено на заседании кафедры информатики 08.04.2013 з аведующий кафедрой а.Ю.Выжигин

МосГУ Зимняя экзаменационная сессия 2012-2013 учебного года Кафедра информатики и математики

Д исциплина Теория вероятностей и математическая статистика Факультет Экономики и управления Курс 2 дневное отделение

Экзаменационный билет № 2

1. Полная группа несовместных событий и полная вероятность.

2. Математическое ожидание дискретной случайной величины. Основные свойства математического ожидания

3. Решите задачу: В первой урне 8 черных и 2 белых шаров. Во второй урне 3 белых и 7 черных шаров. Из наудачу взятой урны вынули один шар. Тогда вероятность того, что этот шар окажется белым, равна …

4. Решите задачу:

Непрерывная случайная величина задана плотностью распределения вероятностей: 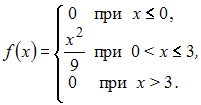Тогда вероятность  равна …

Утверждено на заседании кафедры информатики 08.04.2013 з аведующий кафедрой а.Ю.Выжигин

МосГУ Зимняя экзаменационная сессия 2012-2013 учебного года Кафедра информатики и математики

Д исциплина Теория вероятностей и математическая статистика Факультет Экономики и управления Курс 2 дневное отделение

Экзаменационный билет № 3

1. Вычисление вероятностей гипотез (формула Байеса).

2. Дисперсия дискретной случайной величины. Основные свойства дисперсии. Стандартное (среднее квадратическое) отклонение.

3. Решите задачу: Непрерывная случайная величина  задана функцией распределения вероятностей: 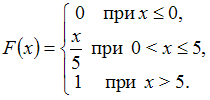Тогда ее плотность распределения вероятностей имеет вид …

4. Решите задачу:

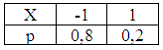
Дискретные случайные величины  и  заданы законами распределения вероятностей: 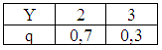Тогда закон распределения вероятностей функции  имеет вид …

Утверждено на заседании кафедры информатики 08.04.2013 з аведующий кафедрой а.Ю.Выжигин

МосГУ Зимняя экзаменационная сессия 2012-2013 учебного года Кафедра информатики и математики

Д исциплина Теория вероятностей и математическая статистика Факультет Экономики и управления Курс 2 дневное отделение

Экзаменационный билет № 4

1. Статистическое определение вероятности.

2. Схема повторных испытаний Бернулли. Формула биномиальной вероятности Бернулли.

3. Решите задачу: Двумерная дискретная случайная величина задана законом распределения вероятностей: Тогда вероятность равна …

4. Решите задачу:

Непрерывная случайная величина  задана плотностью распределения вероятностей: 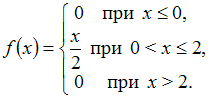Тогда ее дисперсия равна …