
- •Л абораторная работа № 2
- •Применение линейной теории полезности для принятия решения о распределении ресурсов
- •Пример постановки задачи на составление оптимального плана
- •Задание примерно такого типа будет в Вашем варианте!
- •Предварительный этап – сведение к задаче линейного программирования
- •Вводим переменные
- •Составляем функцию полезности
- •40Х0 – прибыль от выпуска х0 единиц продукта а,
- •60Х1 – прибыль от выпуска х1 единиц продукта б.
- •Определяем целевой критерий
- •Определяем ограничения
- •Записываем математическую форму задачи
- •Решение задачи в программе Excel
- •Обратите внимание!
- •Обратите внимание!
- •Решение задачи в программе Mathcad
- •Обратите внимание!
- •Обратите внимание!
- •Отчетность по лабораторной работе
Обратите внимание!
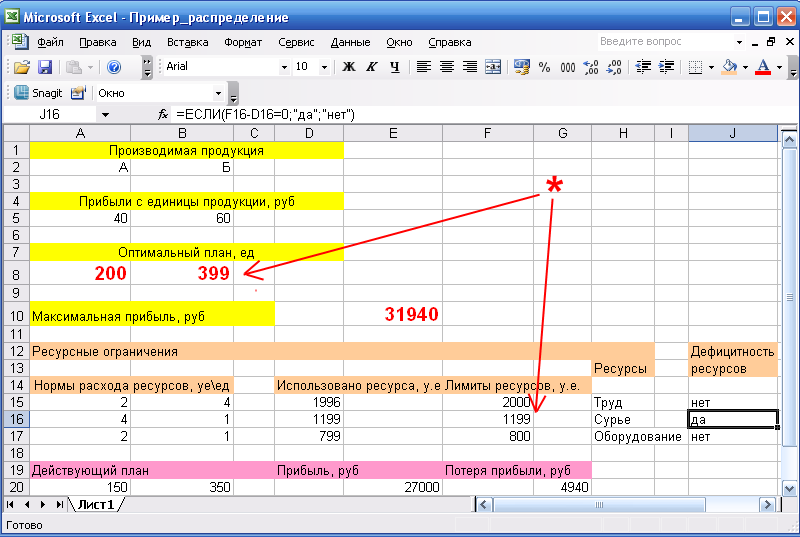
Если использованный ресурс (левая часть неравенства-ограничения) в результате расчетов оказался равным лимиту (правой части неравенства-ограничения), то соответствующий ресурс дефицитный, т.к. используется полностью. В данном примере все дефицитны труд и оборудование, недефицитным оказалось сырье.
Этот вывод требуется для выполнения задания б) – см. пример постановки задачи.
Для автоматической проверки дефицитности ресурсов задайте в каждой строке в ресурсными ограничениями (здесь это строки 15-17) логическую формулу типа «=ЕСЛИ(F15-D15=0; «дефицитный»; «недифицитный»). В OpenOffice вместо «ЕСЛИ» ставится «IF».
Обратите внимание!
 Постепенно изменяя правую часть
какого-либо ограничения (см. лимит
ресурса по заданию г)) и выполняя каждый
раз поиск решений определите примерные
границы изменений, за пределами которых
план изменяется, а в пределах которых
план не изменяется. Это требуется для
задания г).
Постепенно изменяя правую часть
какого-либо ограничения (см. лимит
ресурса по заданию г)) и выполняя каждый
раз поиск решений определите примерные
границы изменений, за пределами которых
план изменяется, а в пределах которых
план не изменяется. Это требуется для
задания г).
Здесь лимит с 1400 уменьшался до 1200 без измене-ния оптимального плана (А – 200, Б – 400), но при дальнейшем снижении план изменился (см. *). Значит, нижняя граница лимита – 1200 ед. Верхняя граница не определяется. Это и понятно – ведь ресурс недифицитный! Для дефицитных ресурсов окажется, что нижняя граница совпадает с заданной (т.е. малейшее ее уменьшение приведет к изменению оптимального плана), а вот верхнюю границу придется подобрать.
Аналогично выполняем задание д), но для этого постепенно изменяем заданный коэффициент целевой функции (прибыль, цену, выручку, производительность и т.д.). При этом оптимальная полезность обязательно изменится, но наблюдать требуется только за планом!
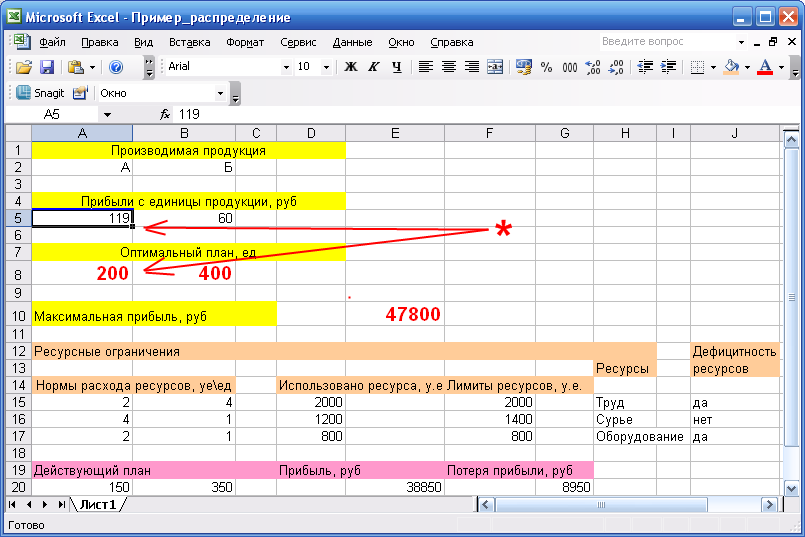
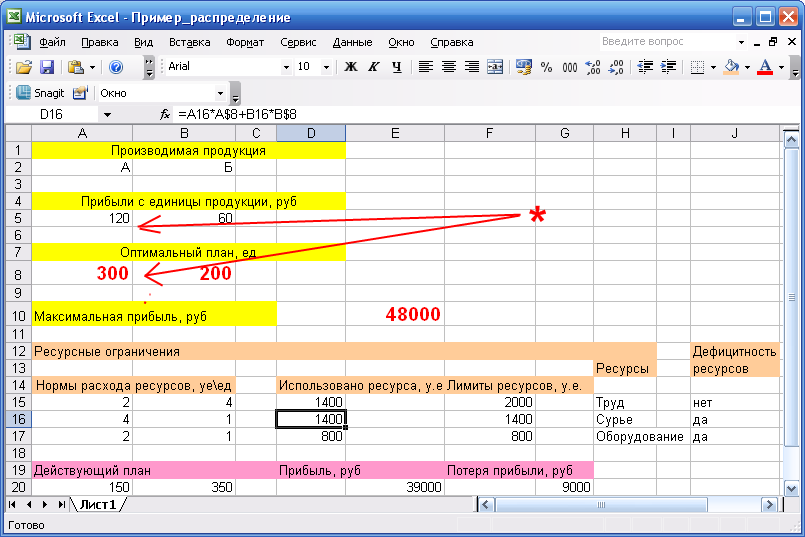
В данном примере при увеличении прибыли от реализации продукции А с 40 до 119 оптимальный план не изменяется, но если прибыль равна 120, то план другой. Значит верхняя граница прибыли от А, при которой оптимальный план неизменен, равна 119.
Аналогично устанавливается нижняя граница прибыли от А – 30 уе.
К началу ↑
Решение задачи в программе Mathcad
П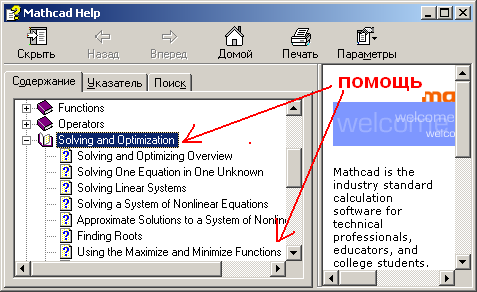 ри
работе с программой помните:
ри
работе с программой помните:
используемая нами версия программы – портативная, т.е. запускается без установки с «флэшки»;
все расчетные формулы и соотношения должны быть введены английскими буквами;
программа воспринимает одну и ту же букву, записанную как прописную и как строчную, по-разному;
каждая формула должна быть набрана в одной рамке и без пробелов;
к программе имеется справка.
Н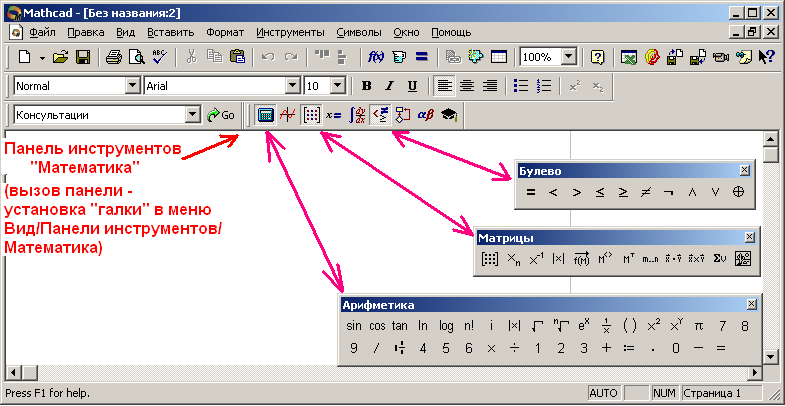 астраиваем
рабочую область программы – через меню
Вид\Панели инструментов\Математическая
открываем 3 необходимых списка (см.
рисунок) и располагаем их справа.
астраиваем
рабочую область программы – через меню
Вид\Панели инструментов\Математическая
открываем 3 необходимых списка (см.
рисунок) и располагаем их справа.
Используя черновик с предварительными рассуждениями, вводим в левую часть экрана следующее:
в
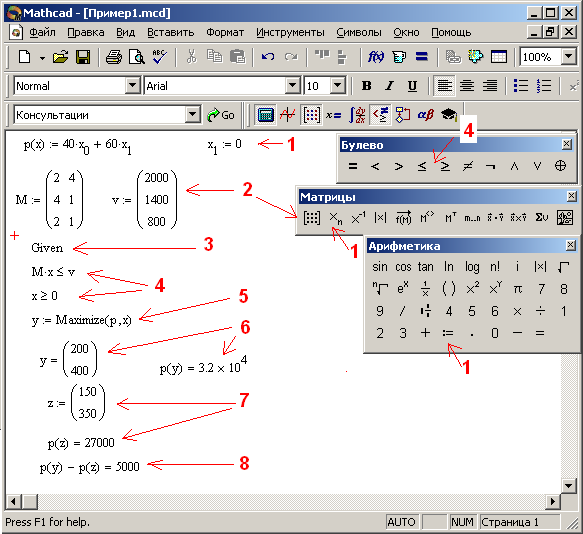 ид
целевой функции и произвольное
значение для последней компоненты её
векторного аргумента
ид
целевой функции и произвольное
значение для последней компоненты её
векторного аргумента
(«:=» - знак присвоения, компоненты вектора – с нижними индексами);
не забывайте вставлять знак умно-жения «*» – с клавиатуры или с па-нели «Калькулятор»\«Арифметика»;
если Вы хотите задать ограничения в матричной форме (см. предварительный этап) матрицу коэффициентов и вектор для ограничений;
команду поиска решения «Given» (вводим вручную);
задаем неравенства-ограничения в векторном виде или перечислив все неравенства в обычном виде;
о
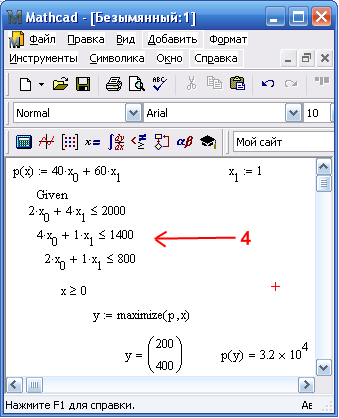 пределяем
оптимальный план или распределение
как вектор, при котором функция р с
аргументом х принимает оптимальное,
т.е. максимальное или минимальное
значение (в последнем случае пишем
«Minimize»); по сути определяем
точку экстремума функции полезности
(если команда «покраснела», то скорее
всего Вы забыли задать значение в п. 1)
или использовали различные типы букв);
пределяем
оптимальный план или распределение
как вектор, при котором функция р с
аргументом х принимает оптимальное,
т.е. максимальное или минимальное
значение (в последнем случае пишем
«Minimize»); по сути определяем
точку экстремума функции полезности
(если команда «покраснела», то скорее
всего Вы забыли задать значение в п. 1)
или использовали различные типы букв);
вычисляем оптимальный план или оптимальное распределение (точка экстремума целевой функции) и целевое значение полезности (максимум прибыли, выручки и т.п.); здесь – максимум прибыли («=» – автоматическое вычисление результата; заметьте, что знак «=» с панели «Булево» или «Логическая» наряду со знаками неравенств используется для задания ограничений);
определяем действующий или предварительный план и соответствующую ему полезность;
вычисляем величину упущенной выгоды.
В данном случае с учетом введенных обозначений для достижения максимальной прибыли 32000 (это прогноз при принятии нового плана или распределения) рекомендуется применить план выпуска: А – 200 ед, Б – 400 ед. (это рекомендация к принятию решения). Т.е. принятие этого плана позволяет ликвидировать ежедневную упущенную выгоду (потерю прибыли) в размере 5000 уе. (это обоснование предложенного решения).
