Теория вероятности и матстатистика. Вариант 17.

Задание 1.17. В первой урне 5 белых и 3 черных шаров, а во второй урне 4 белых и 9 черных шаров. Из первой урны вынимают случайным образом 2 шара, а из второй 3 шара. Найти вероятность того, что среди вынутых шаров

А) все шары одного цвета;

Б) только три белых шара;

В) хотя бы один белый шар.

Решение:

А) Вероятность что из первой урны вынут 2 белых шара равна количеству сочетаний из 5 по 2 делённому на количеству сочетаний из 8 по 2, т.е. количеству всех комбинаций из 2 белых шаров делённому на количество всех комбинаций из 2 любых шаров:

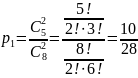
Аналогично находится вероятность извлечения 3-х белых шаров из второй урны:

А чтобы произошло и то и другое, т.е. вынутые из обеих урн шары все были белыми, надо полученные вероятности перемножить:

Точно так же находим вероятность того что все вынутые шары будут чёрными

Теперь поскольку события ВСЕ БЕЛЫЕ и ВСЕ ЧЁРНЫЕ являются несовместными, вероятности надо сложить.

Б) Вероятность того, что из урн извлекут ровно три белых шара состоит из трех несовместных событий:

1 – из первой урны 2 черных, из второй – 3 белых;

2 – из первой урны – 1 белый и 1 черный, из второй – 2 белых и 1 черный;

3 – из первой урны – 2 белых, из второй – 1 белый и 2 черных;

Найдем вероятность появления каждого из событий:

Так как эти события несовместны, то общая вероятность находится по формуле:

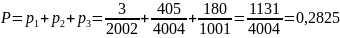
В) Событие, что хотя бы один шар белый – противоположно событию, что все шары черные. Следовательно вероятность будет равна

Задание 2.17. В первой урне 6 белых и 2 чёрных шаров, а во второй урне 3 белых и 8 чёрных шаров. Из первой урны случайным образом вынимают 3 шаров и опускают во вторую урну. После этого из второй урны также случайно вынимают 4 шаров. Найти вероятность того, что все шары, вынутые из второй урны, белые.

Решение:

Сначала рассчитаем вероятность 3 случаев:

1. Того, что из первой урны вынут 3 белых шара

2. Того, что из первой урны вынут 2 белых и 1 черный шар

3. Того, что из первой урны вынут 1 белый и 2 черных шара

B. Теперь посчитаем условные вероятности, рассмотрев 3 случая при условии 3 разобранных: 1. Во вторую урну положили 3 белых шара, тогда у нас есть 6 белых и 8 черных шаров. Вероятность вытащить 4 белых равна:

2. Во вторую урну положили 2 белых и 1 черный шар, тогда у нас есть 5 белых и 9 черных шаров. Вероятность вытащить 4 белых равна:

3. Во вторую урну положили один белый и два черных шаров, тогда у нас есть 4 белых и 10 черных шаров. Вероятность вытащить 4 белых равна:

Теперь, учитывая то, что а₁ состоялось при условии р₁, а₂ – р₂, а₃ – р₃, общая вероятность вытащить 4 белых шара из второй урны по формуле полной вероятности равна

Задание 3.17. В каждом из n независимых испытаний событие A происходит с постоянной вероятностью p. Найти вероятность того что в данной серии испытаний событие А произойдёт:

А) точно N раз;

Б) больше чем M раз и меньше чем N раз;

В) больше чем N раз.

Найдем необходимые значения, согласно своему варианту:

n = 700+17*10 =870, р = 0,35+17*0,02 =0,69, N = 270+17*10 = 440, М = 440 – 40 – 17 = 383