2.5. Запись результатов измерений.

Стоит сказать несколько слов о записи результатов измерений. Вычисленная величина определяет точность, с которой есть смысл вычислять потому что знание погрешности спасает от лишних промежуточных вычислений. Легко увидеть, например, что запись М = М = (20,1653 ± 0,54) Н  м бессмысленна. Вычисление среднего значения в этом случае нужно делать с точностью до второго знака после запятой или, максимум, до третьего. При погрешности 0,54 последние две цифры числа 20,1653 не значат абсолютно ничего. Правильная запись результата была бы М = (20 ± 0,5) Н  м.

Еще примеры: 1) если = 157,3 гсм² й = 1,5 г  см²,

результат = (157,3 ± 1,5) г  см²;

2) если 135 мг, =0,0005 мг,

то результат m = (135,0000 ± 0,0005) мг.

В процессе записи результата среднее значение и средняя абсолютная погрешность округляются к тому знаку, в котором начинается значимая цифра в числе а сами и вычисляются с точностью, большей только на один порядок, чтобы знать, как их округлить.

Во многих случаях преимущественно отмечают величину погрешности в процентах от измеряемой величины.

Например, вес гири 2,00 ± 0,10 г или 2,00 г ± 5%.

2.6. Графические методы обработки результатов.

Очень важным методом обработки результатов опыта является представление их в виде графика. График позволяет наглядно показать функциональную зависимость и определить ее параметры (например, угловой коэффициент в случае линейной зависимости).

1. График должн выполняться на миллиметровой бумаге (размер порядка 10 см х 10 см).

2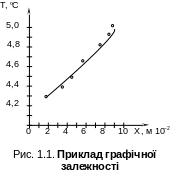 . Обычно используют прямоугольную систему координат с одинаковыми масштабами по осям x и у. Значения аргумента обычно откладывают по оси абсцисс, функции – по оси ординат.

3. На координатных осях необходимо указывать не только величины, которые откладывают, но и единицы их измерения.

4. Масштаб принципиально может быть каким угодно, но выбирать его нужно так, чтобы получить приблизительно равные размеры графика по длине и по высоте.

Если первое значение измеряемой величины очень отличается от нуля и если изменение этой величины незначительно, отсчет в начале координат нужно начинать не от нуля, а от какого-то значения, близкого к первому измеряемому значению данной величины. Когда масштаб избран, нужно разделить оси в избранном масштабе на равные интервалы и надписать на осях значение этих интервалов (рис. 1.1).

5. На основе данных табл. 1.2 на график наносят точки (маленькими кружочками), которые рекомендуется помечать чернилами, а кривую проводить так, чтобы нанесенные точки выделялись четко. Поскольку все измерения выполнены с той или другой погрешностью, то может иметь место некоторый разброс точек (они не укладываются точно на одной кривой). В этом случае нужно проводить между точками плавную линию так, чтобы как можно большее количество точек легли на эту линию, а другие распределились приблизительно равномерно выше и ниже от нее (см. рис. 1.1). С помощью полученного графика можно для любого промежуточного значения одной из величин найти соответствующее ему значение другой величины.

Таблица 1.2

Результаты измерений

T,ºC	X, м
4,30	0,018
4,38	0,034
4,49	0,047
4,64	0,059
4,82	0,074
4,95	0,082