2.2. Погрешность измерений.

В результате несовершенства измерительных приборов, не контролированных колебаний условий измерений, трудностей учета всех побочных явлений во время измерений, несовершенства органов чувств наблюдателя и из-за других причин результат измерения не является точным, а содержит определенную погрешность (ошибку). Поэтому задача измерений заключается не в определении правильного значения измеряемой величины, а в установлении интервала, внутри которого находится правильное значение этой величины. Теория погрешностей указывает на то, как следует осуществлять измерение и их обработку, чтобы величина этого интервала была минимальной.

Погрешности, которые возникают во время измерения, разделяются на два больших класса:

1. Систематические погрешности – ошибки, которые хранят величину и знак от опыта к опыту. Природа и характер систематических ошибок могут быть известны. К ним принадлежат ошибки, вызванные неточностью градурования измерительных приборов, постоянным и односторонним внешним влиянием, личными качествами наблюдателя. Такие погрешности можно учесть, а следовательно и устранить.

Уменьшить вклад систематических погрешностей путем повторения опыта, конечно, нельзя. Для этого нужно усовершенствовать прибор или изменить методику измерений.

Примеры систематических погрешностей: ошибки, связанные с сдвигом нулевой точки термометра, с неправильным весом гирь, с неточным распределением шкалы измерительных линеек и так далее

2. Случайные погрешности – ошибки, которые непредвиденным образом изменяют свою величину (и знак!) от опыта к опыту. Случайные погрешности зависят от неточности измерительных приборов, от несовершенства наших органов чувств и от непрерывного действия внешних условий, которые изменяются (изменения температуры, давления, влажности и тому подобное). Такие ошибки можно свести к минимуму, но полностью устранить их невозможно. В процессе многоразовых измерений они подчиняются статистическим законам и их влияние на результат измерения можно учесть.

Разновидностью случайных погрешностей являются так называемые промахи (операторские ошибки), или грубые ошибки, которые возникают через невнимательность наблюдателя во время включения прибора, отсчета по шкале или записи результата. Например, отсчет по шкале 18 вместо 13, запись результата 17,5 вместо 1,75. Промахи оказываются в резком отличии результата одного из измерений от других и должны быть исключены до математической обработки.

Полностью устранить случайные погрешности невозможно. Поэтому появляется задача получения по данным измерений как можно более точного значения измеряемой величины и оценки его точности. Это задача решается методами математической обработки результатов измерений.

2.3. Оценка точности результата многоразовых прямых измерений.

Теория погрешностей применяется только для случайных погрешностей, потому в дальнейшем следует считать, что грубые промахи и систематические погрешности полностью устранены из измерений.

Абсолютная погрешность. Пусть сделано N измерений некоторой величины, правильное значение которой а. В результате измерений будет получен ряд приближенных значений а₁, а₂ . а_n этой величины. Наиболее вероятным значением измеряемой величины является ее среднее арифметическое значение :

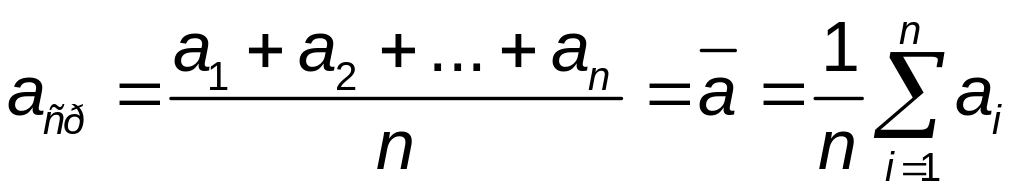. (1.1)

Разница между значением, полученным в каждом измерении, и средним арифметическим значением величины называется абсолютной погрешностью отдельного измерения:

– абсолютная погрешность 1-го измерения;

– абсолютная погрешность 2-го измерения;

– абсолютная погрешность n-го измерения.

Средней абсолютной погрешностью измерения является среднее арифметическое абсолютных значений погрешностей отдельных измерений:

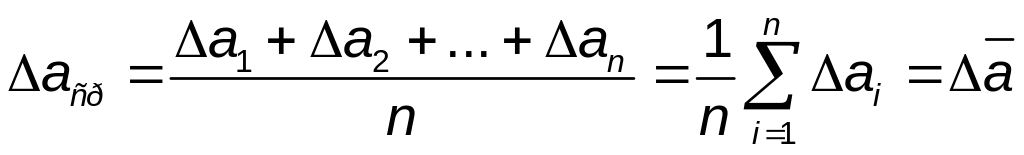. (1.2)

В случае бесконечно большого количества измерений:

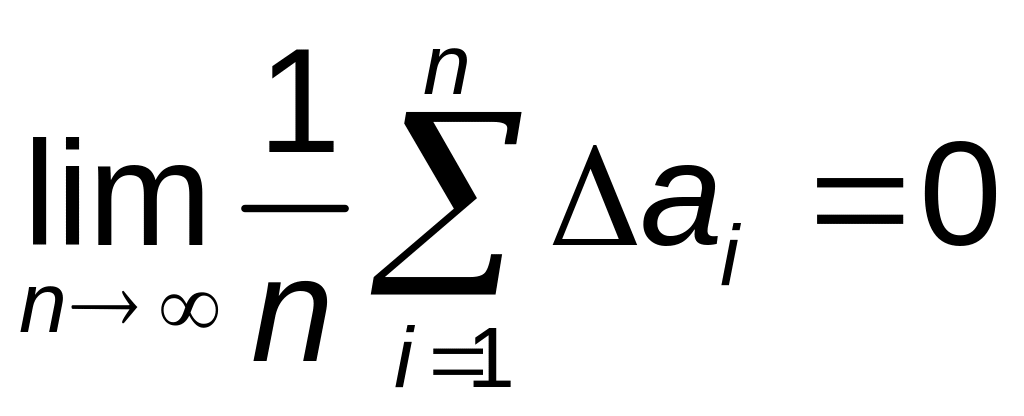. (1.3)

Тогда среднее арифметическое значение результатов отдельных измерений точно равняется настоящему значению измеряемой величины а.

Практически n всегда конечное, так что остается наиболее вероятным значением измеряемой величины а. Для определения максимальной величины все слагаемые в выражении (1.2) нужно сложить по модулю независимо от их знака, то есть:

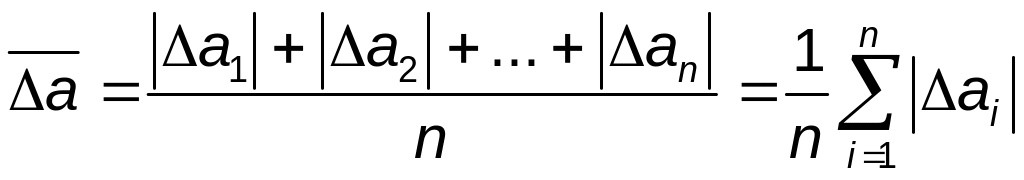. (1.4)

При достаточно большом количестве измерений случайные погрешности будут равговероятны как в сторону увеличения, так и в сторону уменьшения значения измеряемой величины. Это значит, что правильное значение измеряемой физической величины находится в интервале:

Конечный результат измерений принято записывать:

(1.5)

С увеличением количества измерений средняя абсолютная погрешность уменьшается, следовательно, измерение нужно выполнять столько раз, чтобы она равнялась погрешности прибора.

Если в результате измерений выходит ряд абсолютно одинаковых значений измеряемой величины или вычисленная погрешность меньше той, которую дает прибор, то в роли средней абсолютной погрешности выбирается собственная погрешность прибора, которая равняется, как правило, цене (половине цены) деления шкалы прибора (на штангенциркуле, микрометре точность прибора отмечена на самом инструменте). Это же правило применяется к случаям, когда выполняется одно измерение.

Если для определения периода колебаний Т было измерено время одного полного колебания маятника секундомером, цена наименьшего деления которого 0,2 с, то = 0,2 с. Но, измерив время t нескольких n полных колебаний, можно получить значение периода T = t/n в n раз точнее, то есть (с).

Относительная погрешность. Пусть после ряда проведенных измерений длины предмета получено: . В этом случае погрешность 1 мм полностью приемлемая. Но если мы с такой же погрешностью измеряем диаметр шарика, который равняется 3 мм, то полученный результат не может нас удовлетворить. Из приведенного примера следует, что абсолютная погрешность не полностью характеризует качество измерений. Поэтому для полной характеристики измерений наряду с абсолютной погрешностью вводится относительная погрешность .

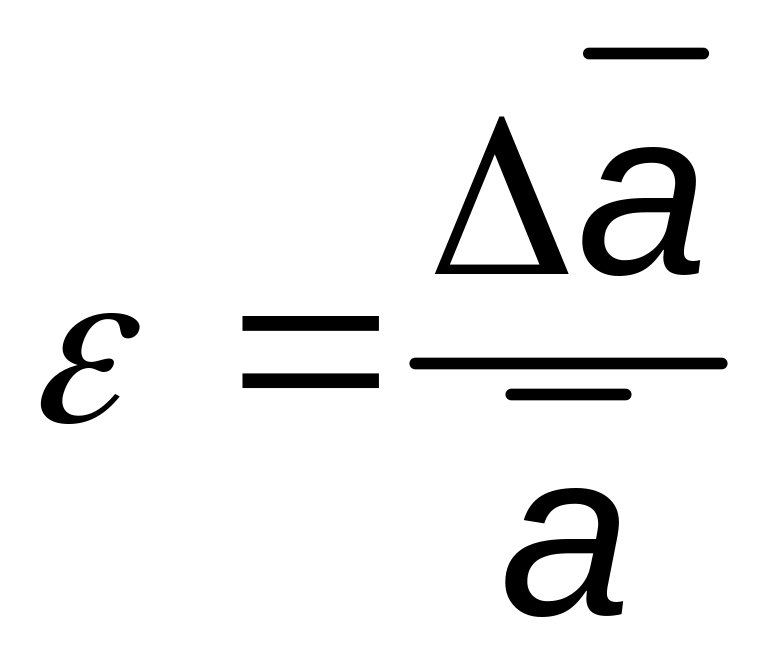Относительная погрешность является отношением средней абсолютной погрешности к среднему значению измеряемой величины . Она показывает, какую часть измеряемой величины составляет средняя абсолютная погрешность, является величиной безразмерной и выражается в процентах:

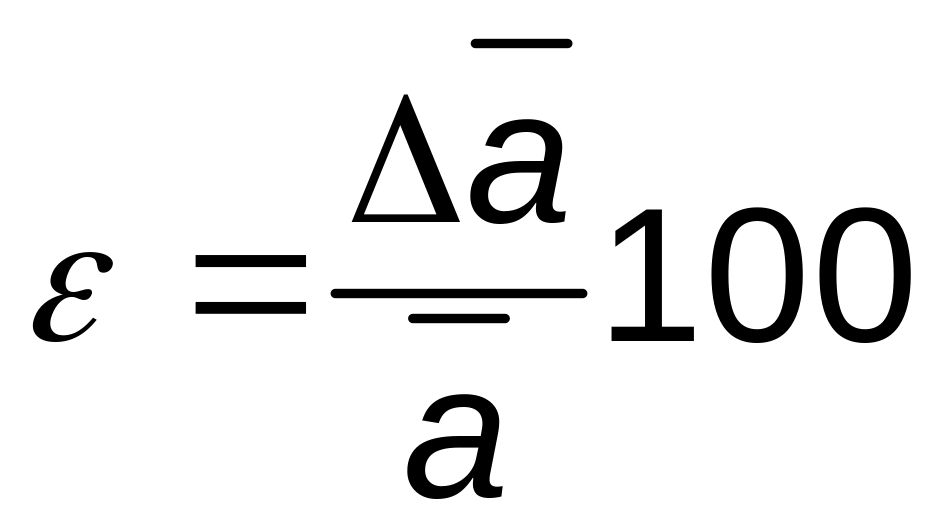%. (1.6)

В приведенном выше примере во время измерения длины предмета погрешность составляет: , а во время измерения диаметра шарика: ,

хотя абсолютные погрешности измерений были одинаковыми.