
- •Методические указания
- •«Пределы и производные функции одной переменной
- •Последовательность, предел последовательности
- •Свойства пределов
- •Неопределенные выражения.
- •Число e
- •Функции одной переменной
- •Обратная функция
- •Предел функции
- •Замечательные пределы
- •Непрерывные функции
- •Точки разрыва функции
- •Монотонные функции
- •Производная и дифференциал функции
- •Рассмотрим функцию . Найдем ее приращение :
- •5. Применение дифференциала к приближенным вычислениям
- •Приложения производной функции
- •Исследование функций и построение графиков Необходимые и достаточные условия возрастания и убывания функции
- •3. Из всех этих значений выбираем наибольшее и наименьшее.
- •Пример. Найти наибольшее и наименьшее значения функции
3. Из всех этих значений выбираем наибольшее и наименьшее.
Замечание. Если непрерывная на отрезке функция имеет во внутренней точке этого отрезка только один экстремум, то в этой точке она имеет наибольшее значение в случае максимума и наименьшее – в случае минимума.
Пример. Найти наибольшее и наименьшее значения функции
![]() на
отрезке
на
отрезке
![]()
![]() ,
,
![]() ,
,
![]()
![]() ;
;
![]() ;
;
![]() ;
;
![]()
Y
наиб.![]() ,
Y
наим.
,
Y
наим.
![]()
Применение теории максимума и минимума к решению задач
Пример
1. Из
квадратного листа жести со стороной
![]() необходимо сделать открытый сверху
ящик наибольшего объёма, вырезая равные
квадратные уголки и загибая жесть.
необходимо сделать открытый сверху
ящик наибольшего объёма, вырезая равные
квадратные уголки и загибая жесть.


Найти сторону вырезаемых квадратных уголков.
Пусть
сторона вырезаемого квадрата
![]() Тогда
Тогда
![]()
сторона ящика.
сторона ящика.
![]() .
Найдём наибольшее значение
.
Найдём наибольшее значение
![]() в интервале
в интервале
![]() .
.
![]() ,
,
![]() ,
,
![]() ,
,
![]() в точке
в точке
![]()
наибольшее значение.
наибольшее значение.
![]()
Пример
2. Найти высоту цилиндра наибольшего
объёма, который может быть вписан в
данный конус с высотой
![]() и радиусом основания
и радиусом основания
![]() .
.
Пусть высота цилиндра - , радиус основания - .
![]() ,
,
![]() подобен
подобен
![]() .
.
![]() ;
;
![]() .
.
![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
следовательно, при
объем цилиндра наибольший.
,
следовательно, при
объем цилиндра наибольший.
Выпуклость и вогнутость графика функции. Точки перегиба
График дифференцируемой функции называется выпуклым (вогнутым) в интервале , если он расположен ниже (выше) любой своей касательной на этом интервале.
Теорема.
Пусть функция
имеет вторую производную
![]() во всех точках интервала
.
Если во всех точках этого интервала
во всех точках интервала
.
Если во всех точках этого интервала
![]() ,
то график функции в этом интервале
выпуклый, если же
,
то график функции в этом интервале
выпуклый, если же
![]() -
вогнутый.
-
вогнутый.
Определение. Точка графика непрерывной функции, отделяющая его выпуклую часть от вогнутой, называется точкой перегиба.
Теорема. (достаточный признак существования точки перегиба).
Если
вторая производная
![]() непрерывной
функции меняет знак при переходе через
точку
,
то точка
непрерывной
функции меняет знак при переходе через
точку
,
то точка
![]() является точкой перегиба графика
функции.
является точкой перегиба графика
функции.
Теорема. (необходимое условие существования точки перегиба).
Пусть
функция
имеет в интервале
непрерывную вторую производную
![]() .
Тогда, если точка
.
Тогда, если точка
![]() является точкой перегиба графика данной
функции, то
является точкой перегиба графика данной
функции, то
![]() .
.
Замечание. Абсциссы точек перегиба графика непрерывной функции следует искать среди тех точек, в которых вторая производная или равна нулю или разрывна (в частности, не существует).
Пример.
![]() ,
,
![]() ,
,
![]() .
.
Асимптоты графика функции
Определение. Асимптотой графика функции называется прямая линия, обладающая тем свойством, что расстояние от переменной точки на графике до прямой стремится к нулю при неограниченном удалении этой точки по графику от начала координат.
Для
того, чтобы прямая
![]() была вертикальной асимптотой, необходимо
и достаточно, чтобы выполнялось хотя
бы одно из условий:
была вертикальной асимптотой, необходимо
и достаточно, чтобы выполнялось хотя
бы одно из условий:
![]() ,
, ![]()
Пример.
![]() ,
,
![]() и
и
![]() являются вертикальными асимптотами.
являются вертикальными асимптотами.
Теорема.
Для того, чтобы прямая
![]() была наклонной асимптотой, необходимо
и достаточно, чтобы выполнялось хотя
бы одно из условий:
была наклонной асимптотой, необходимо
и достаточно, чтобы выполнялось хотя
бы одно из условий:
а)
![]() ;
б)
;
б)
![]()
При
этом
![]() ,
,
![]() или
или
![]() ,
,
![]() .
.
Пример.
![]()
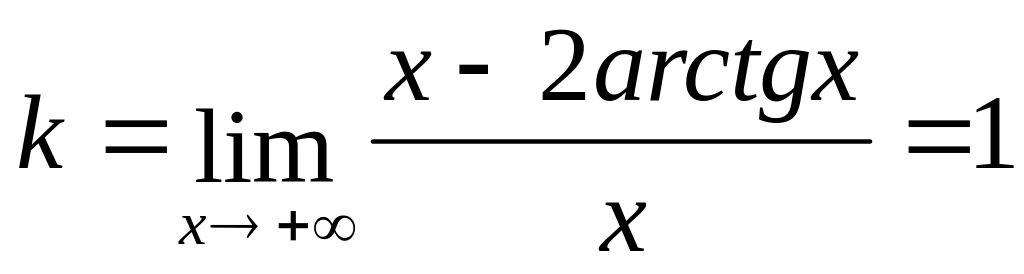 ;
;
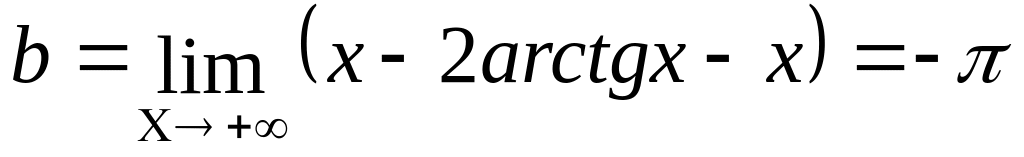
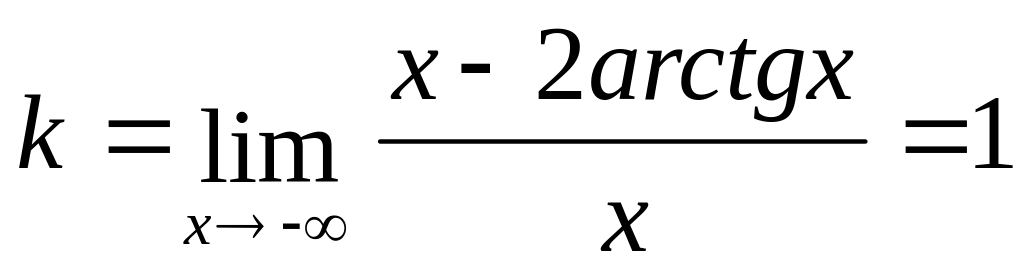 ;
;
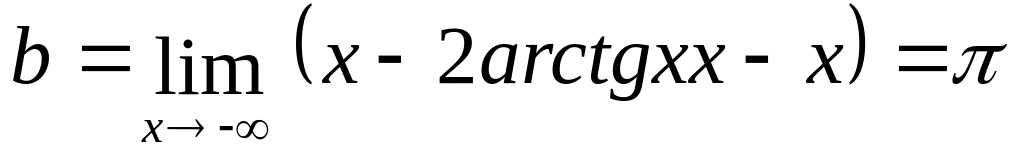
Асимптоты:
![]() ,
,
![]() .
.
План исследования функции.
Область определения функции.
Четность (нечетность) функции.
Периодичность.
Точки пересечения с осями координат.
Монотонность. Экстремальные точки.
Выпуклость(вогнутость) функции. Точки перегиба.
Асимптота.
8. График функции.
Пример.
![]()
Область определения :
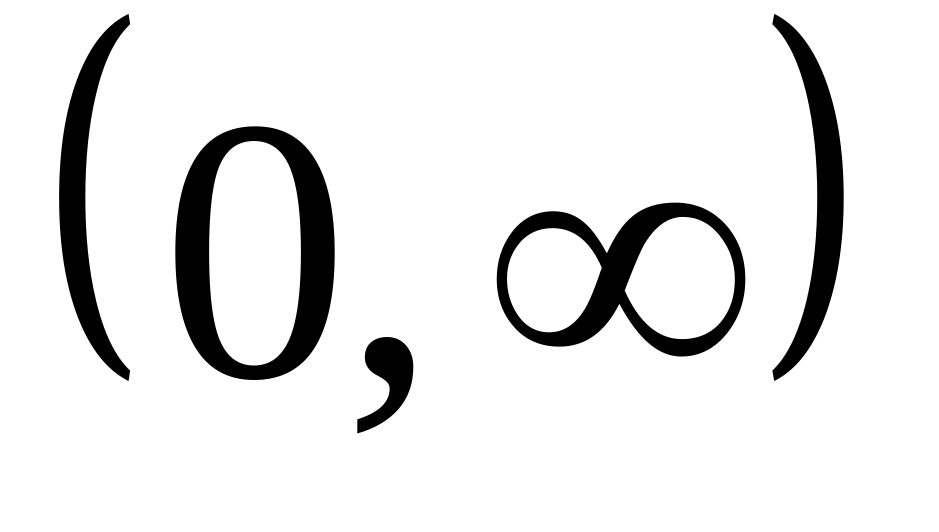 .
.Функция общего вида.
Функция не периодическая.
Имеет точку пересечения с осью Ох :
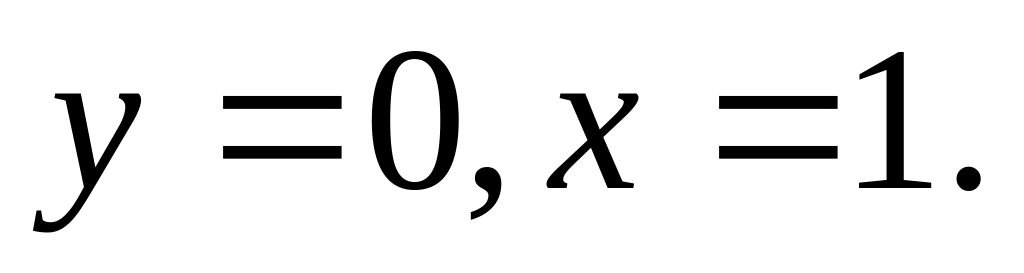
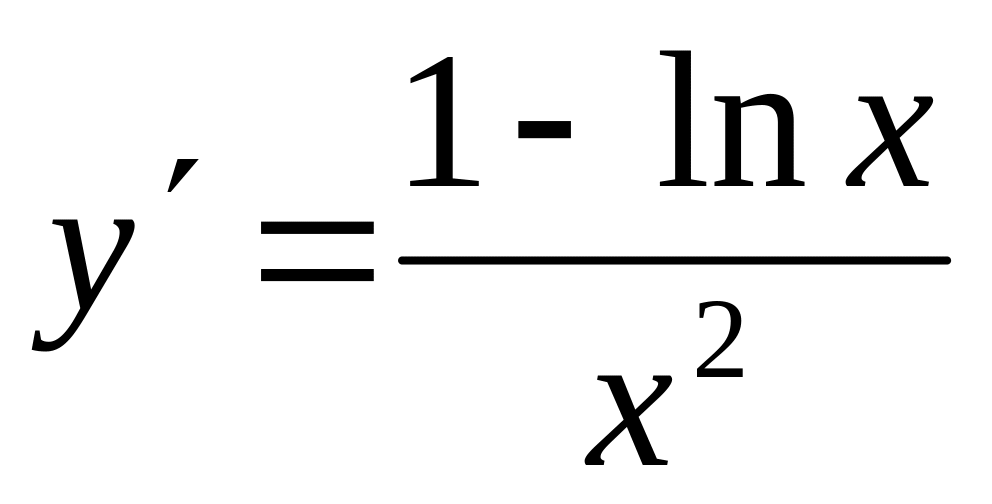 ,
,
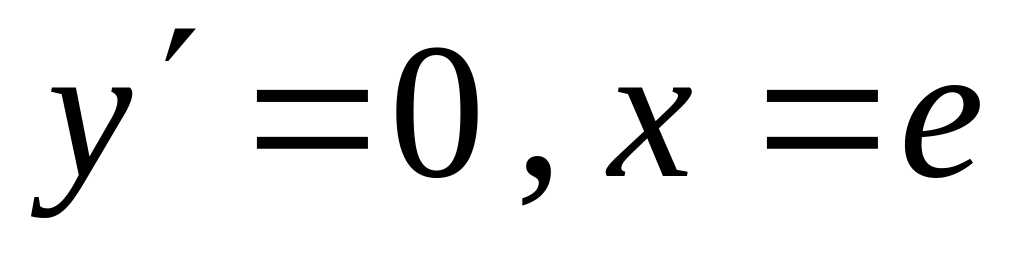 -
критическая точка.
-
критическая точка.
-
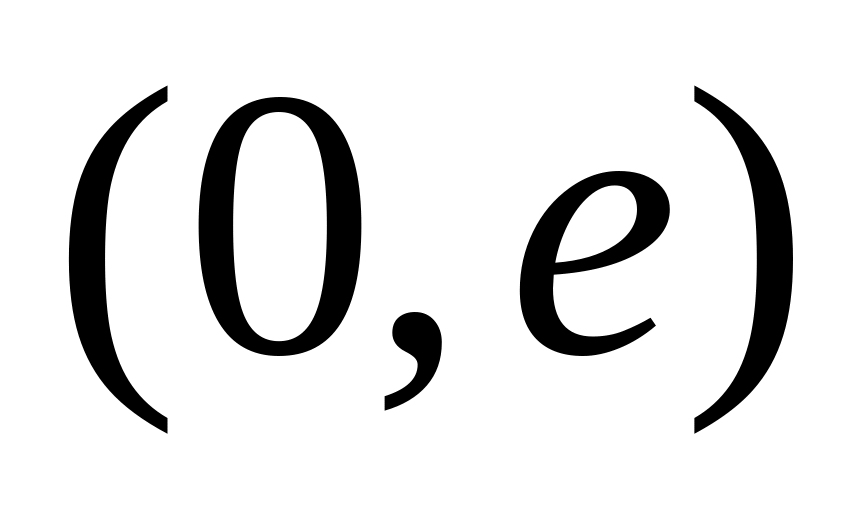
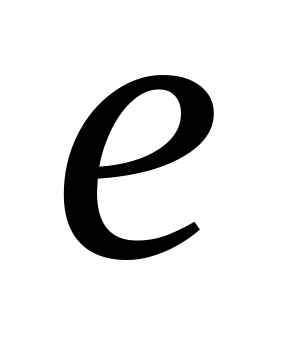
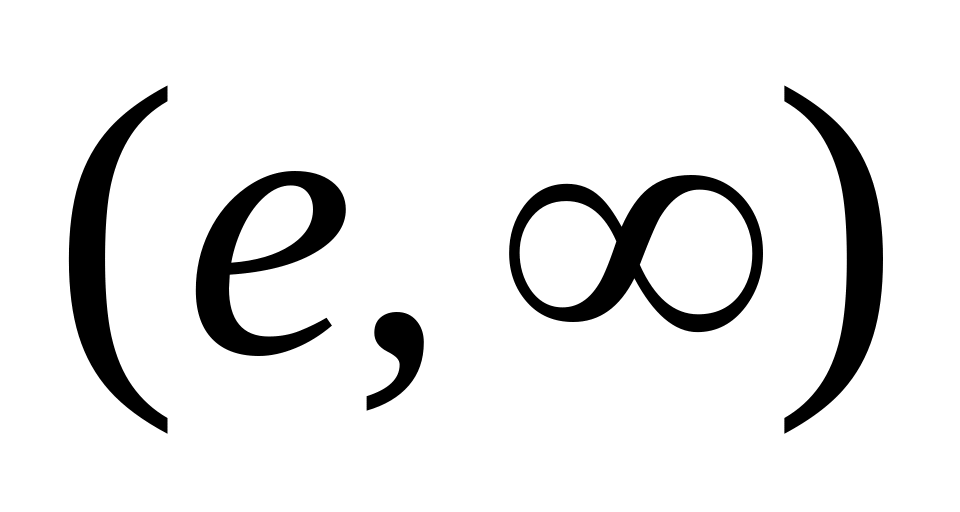
-
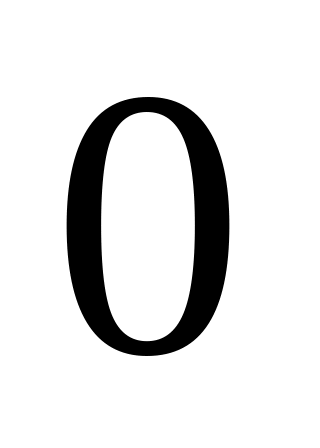
+
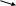
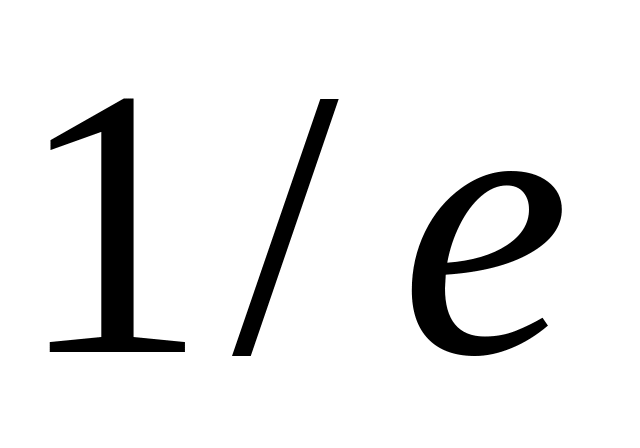
min
-
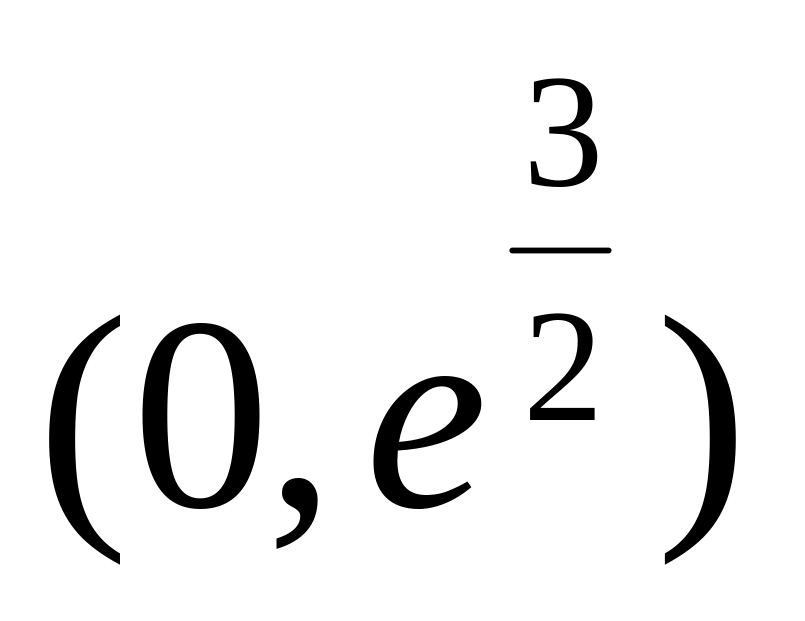
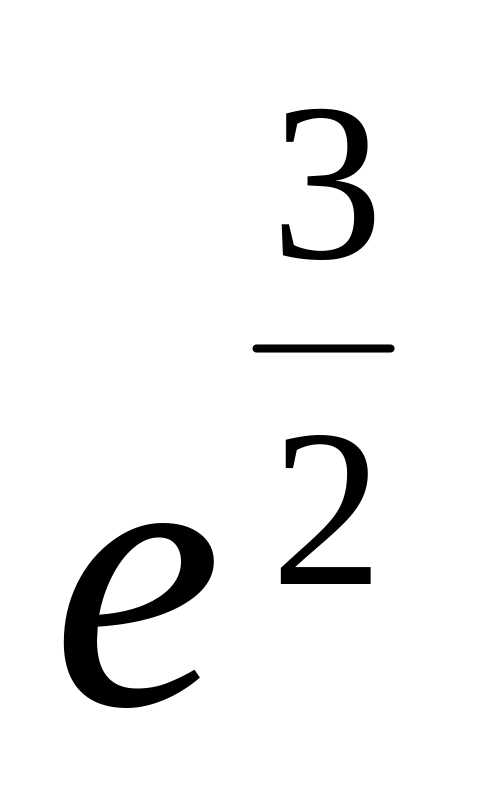
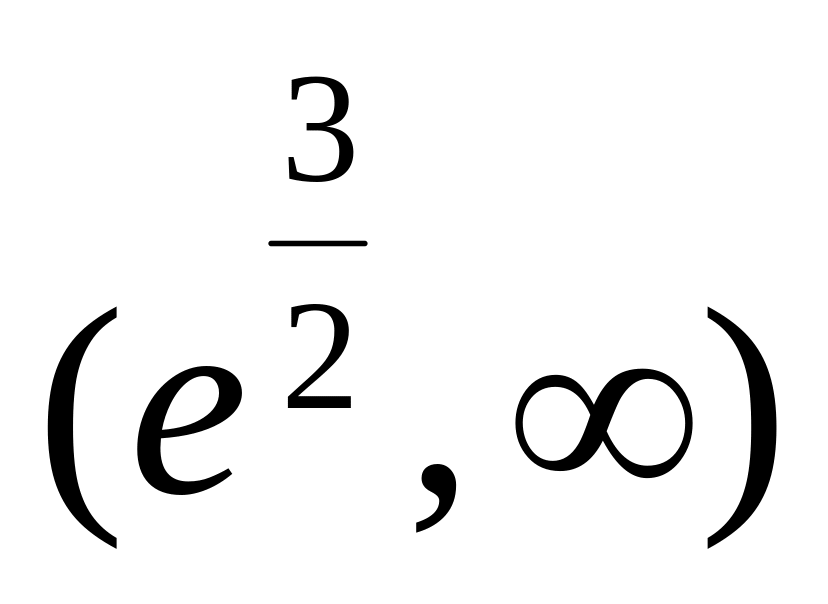
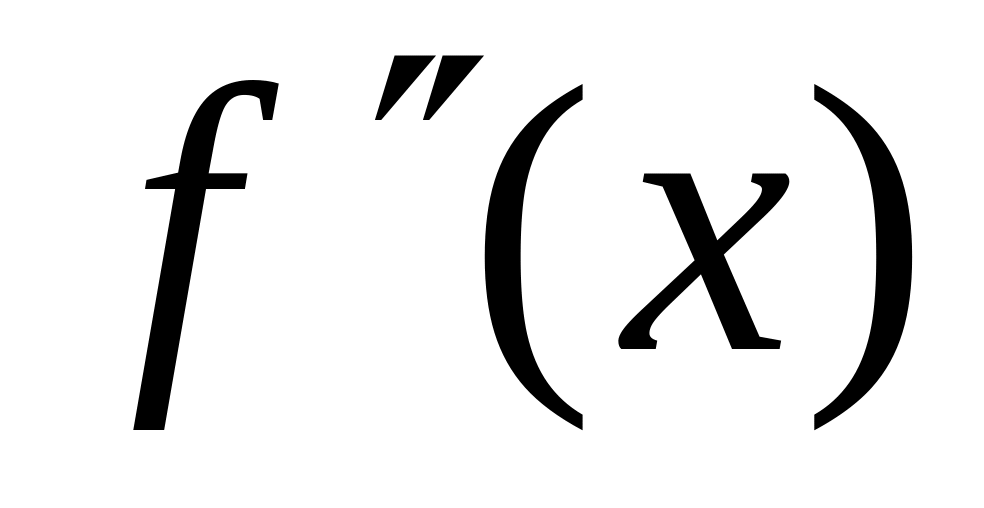
-
+
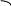
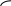


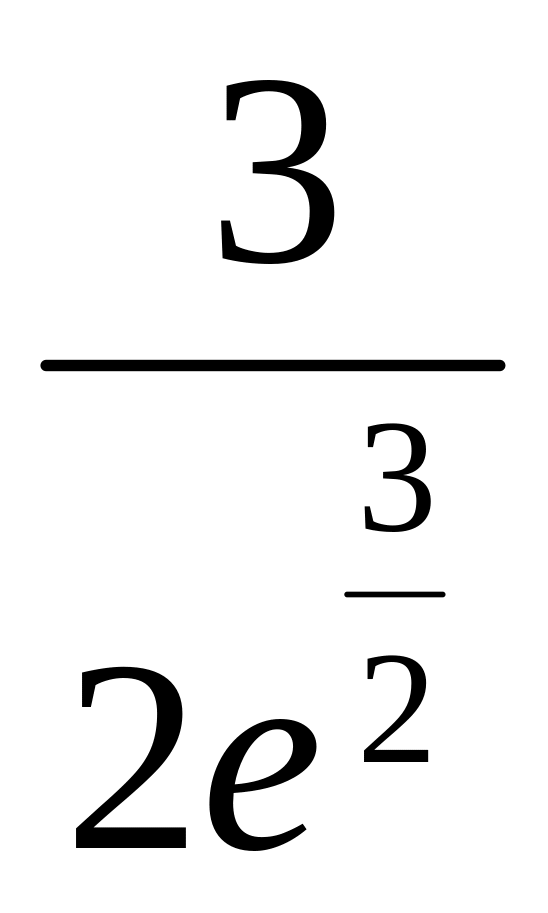
точка
перегиба
Вертикальных асимптот нет.
![]()
![]()
![]() -
горизонтальная асимптота.
-
горизонтальная асимптота.
8. График функции

Пример
2.
![]() .
.
Область определения :
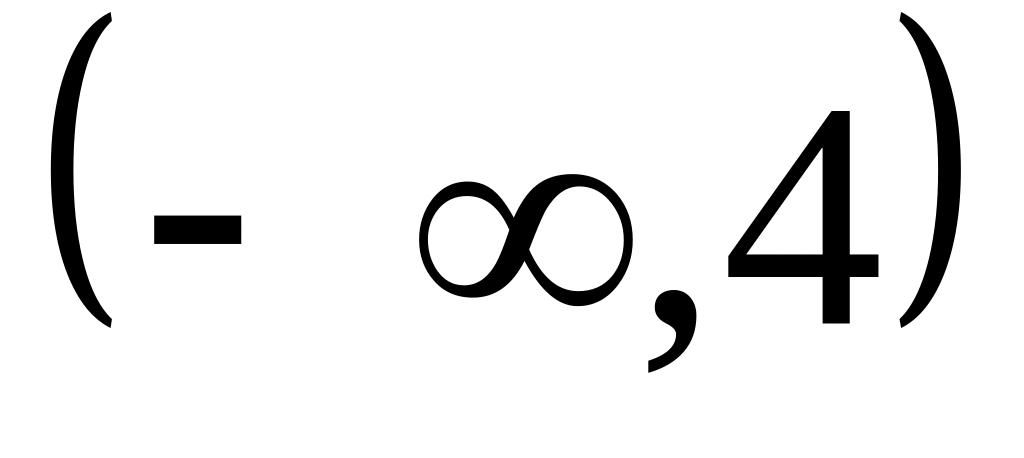
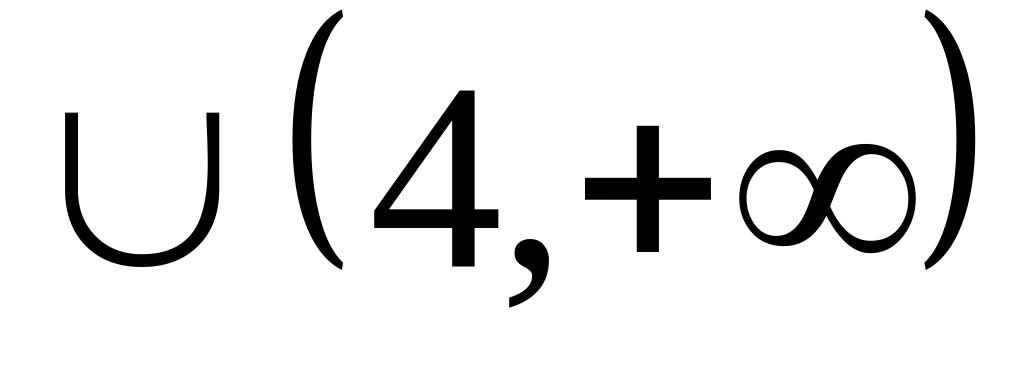 .
.
Функция общего вида.
Функция непериодическая.
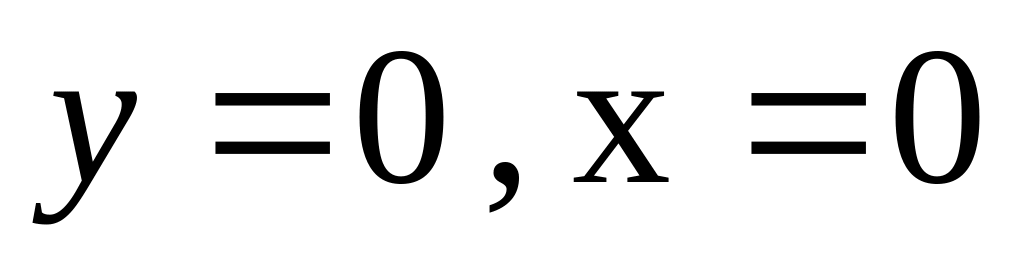 -
точка пересечения с осями координат.
-
точка пересечения с осями координат.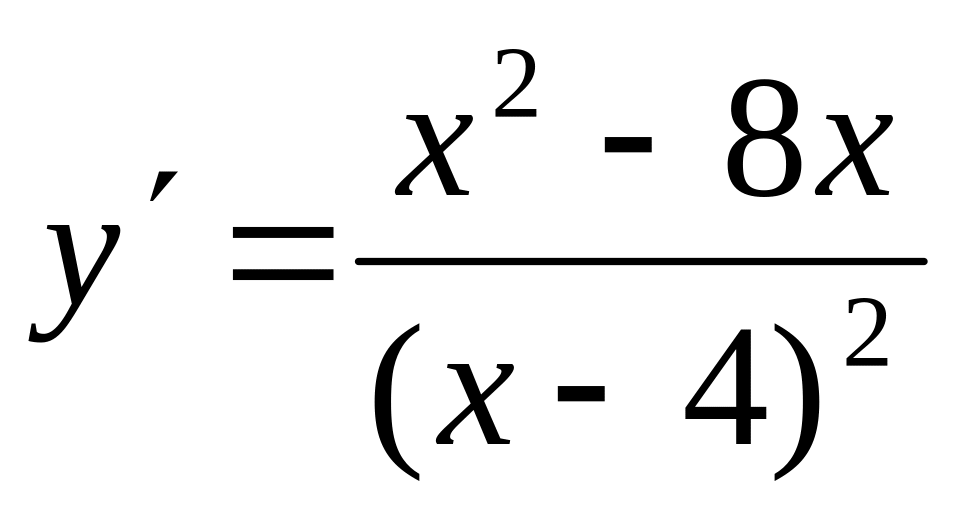 ,
,
 и
и
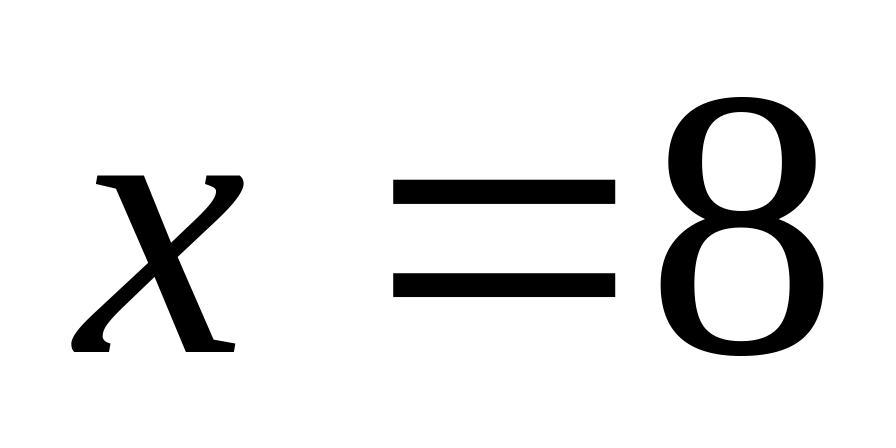 - критические точки.
- критические точки.х

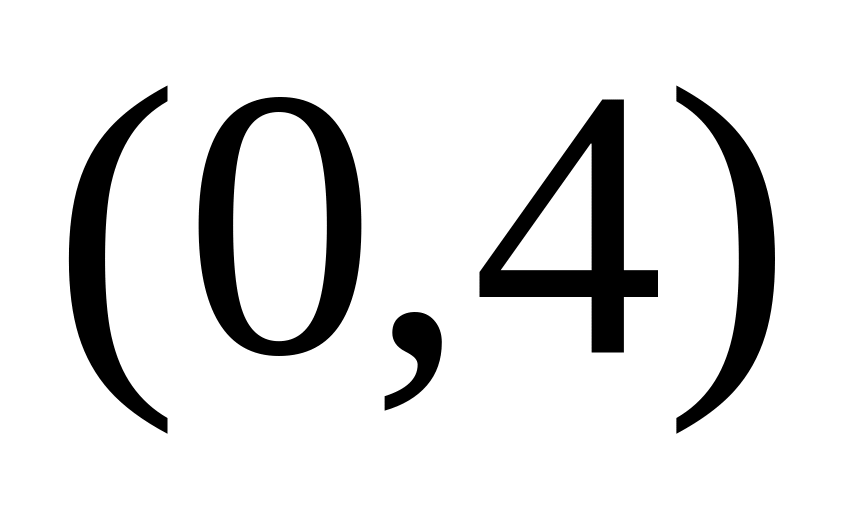
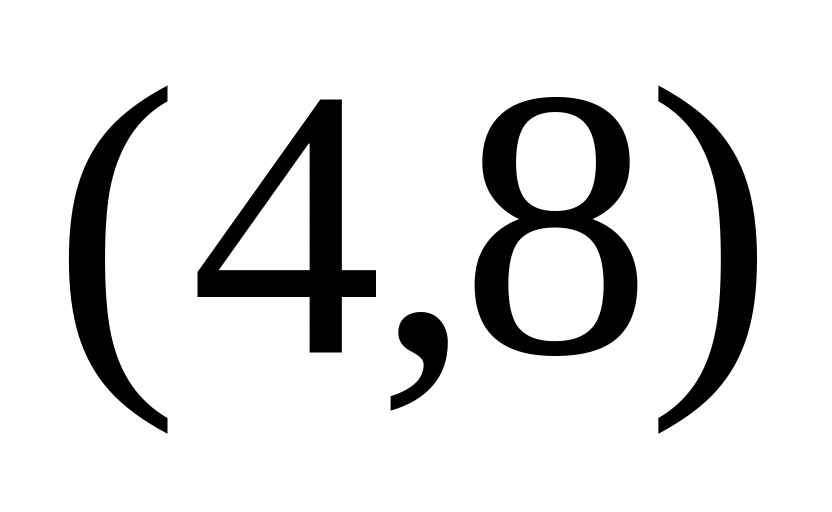
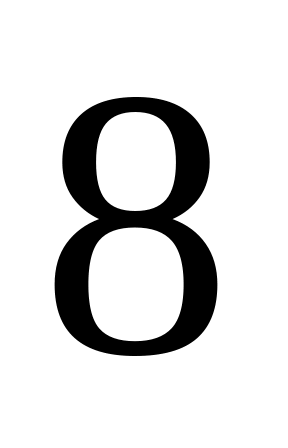 +
+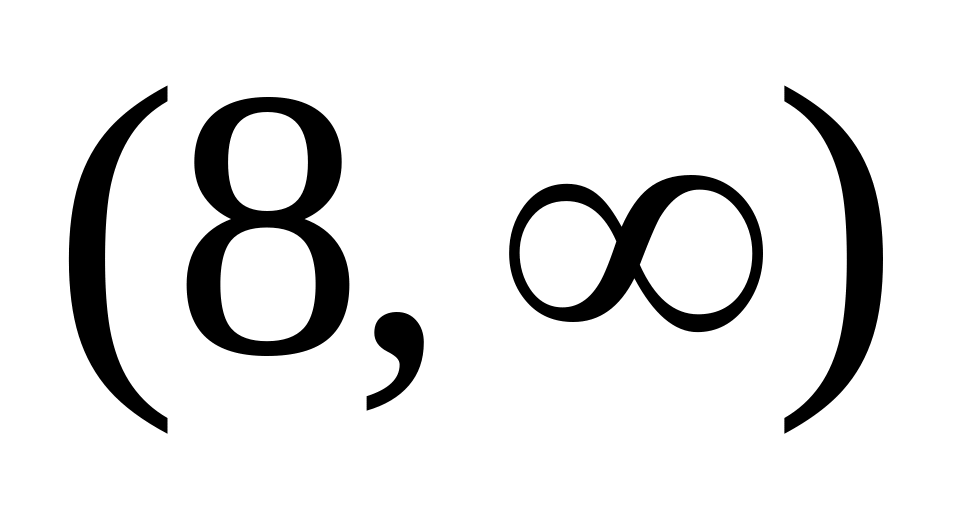
+
-
-
0
+
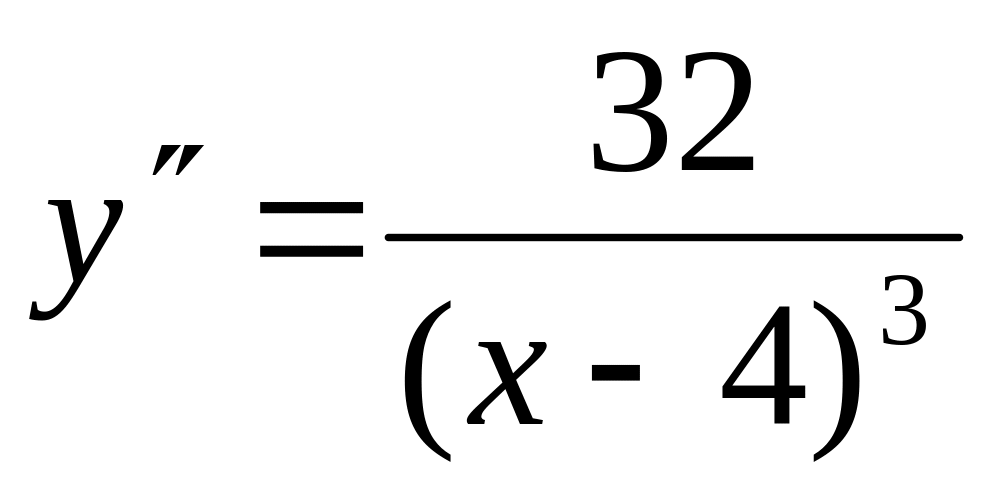 ,
,
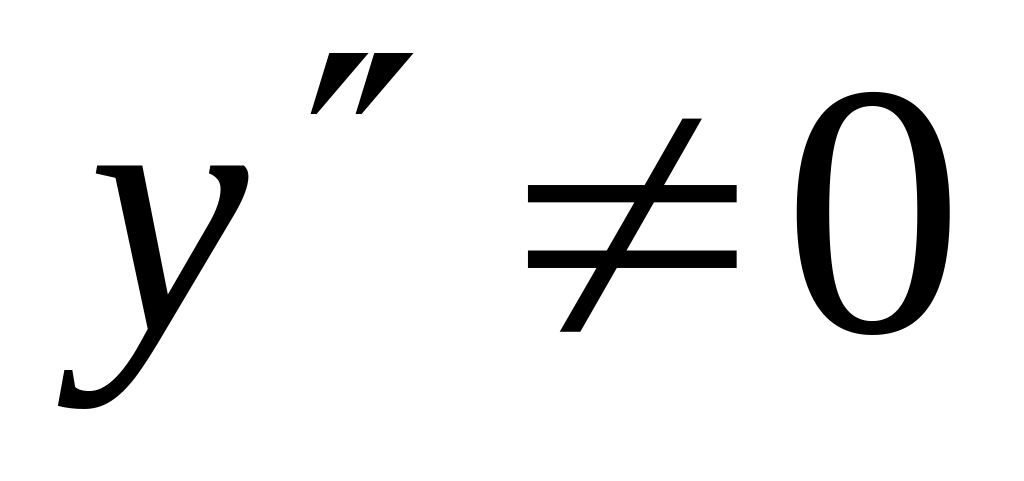 ,
следовательно, у графика функции точек
перегиба нет.
,
следовательно, у графика функции точек
перегиба нет.
-
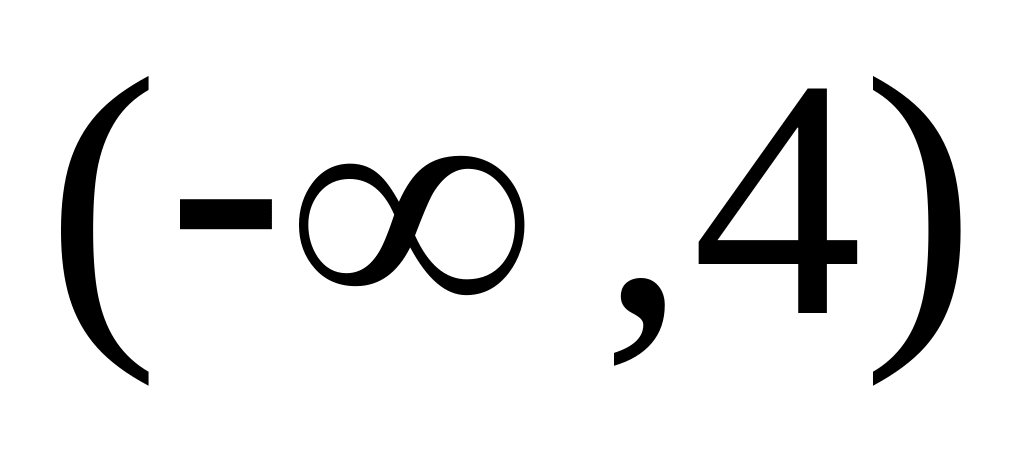
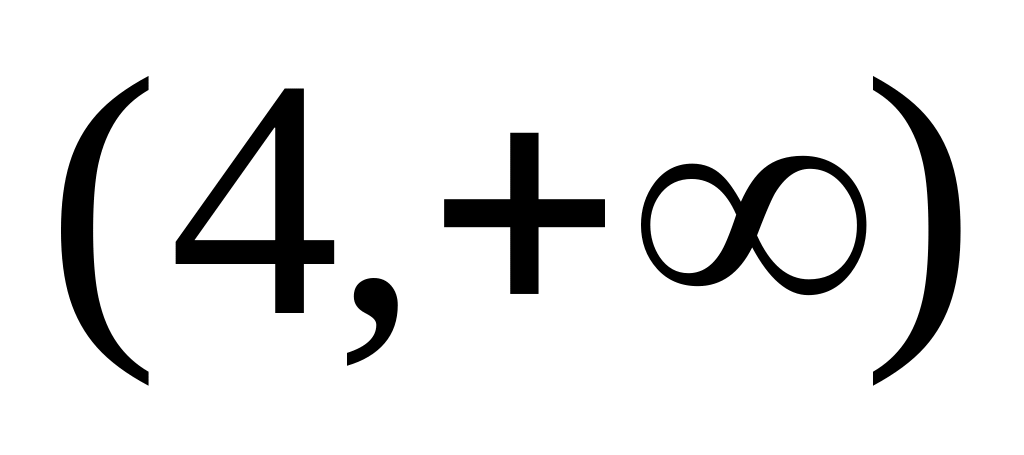
-
+
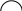

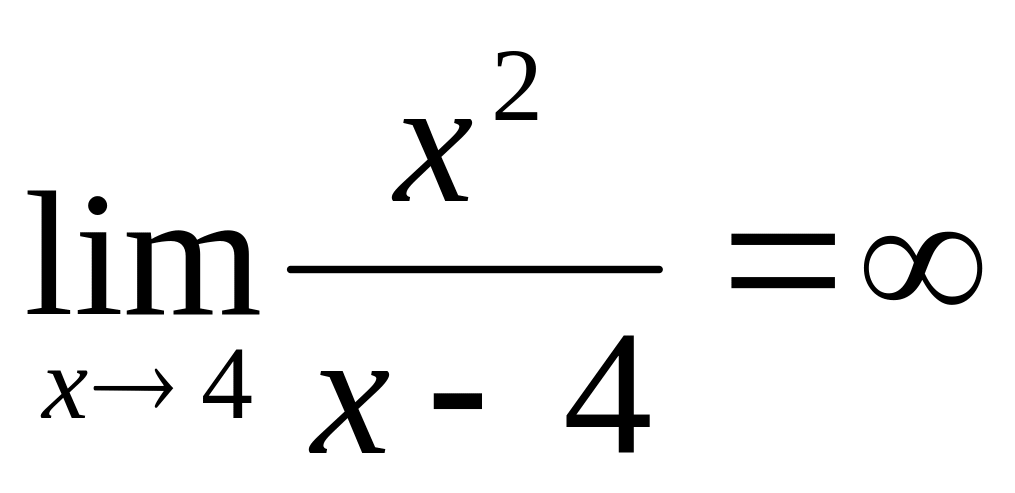 ,
следовательно,
,
следовательно,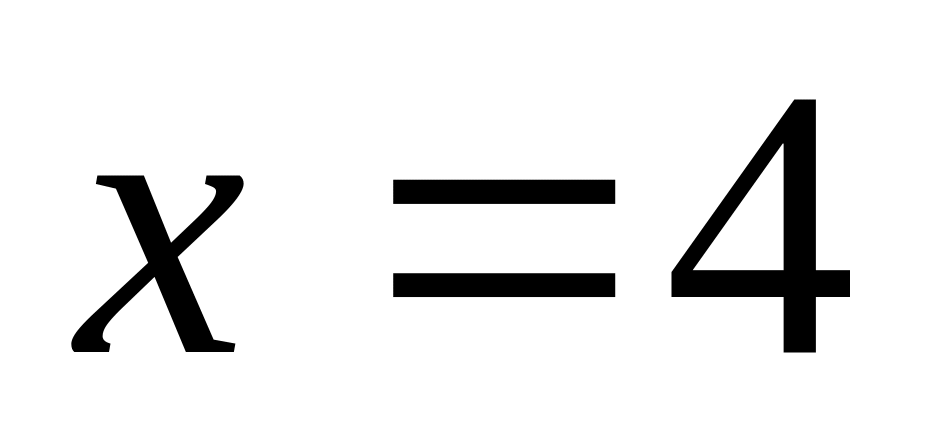 - вертикальная асимптота.
- вертикальная асимптота.
![]() т.е.
т.е.
![]() -
наклонная асимптота.
-
наклонная асимптота.
Г
 рафик
функции
рафик
функции

 У
У
 16
16
 Х
Х
 -4 4 8
-4 4 8
