9.2 Моделирование псевдослучайных чисел и

случайных событий

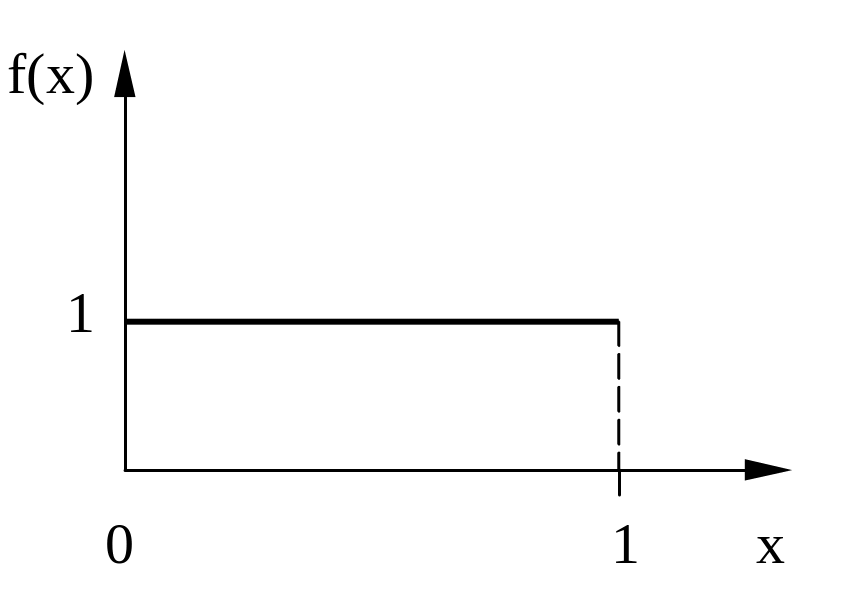
Формирование реализаций любых случайных объектов сводит­ся к выработке и преобразованию с помощью ЭВМ случайных чи­сел. При этом в большинстве случаев исходным материалом для моделирования являются случайные числа с равномерным законом распределения плотности вероятности (f(x)) на отрезке [0, 1] (рисунок 9.1, а).

Для получения (генерирования) равномерно распределен­ных случайных чисел на отрезке [0, 1] существует несколько методов.

1. Разработаны готовые таблицы случайных чисел» В ус­ловиях ЭВМ табличный метод неудобен, так как требует большо­го объема памяти для хранения таблиц.

2. Случайные числа вырабатываются с помощью радиоламп или радиоактивных веществ (физических генераторов случайных чисел). Числа, полученные путем преобразования шумов радио­ламп или излучения радиоактивных веществ, преобразуются в последовательности двоичных разрядов ЭВМ.

а) б)

в) г)

а) равномерное распределение на отрезке [0, 1];

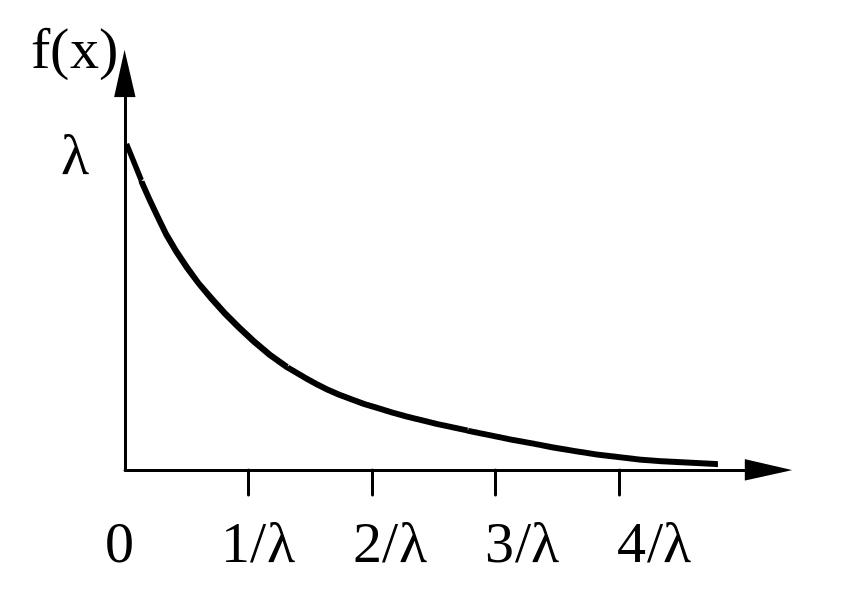
б) экспоненциальное распределение;

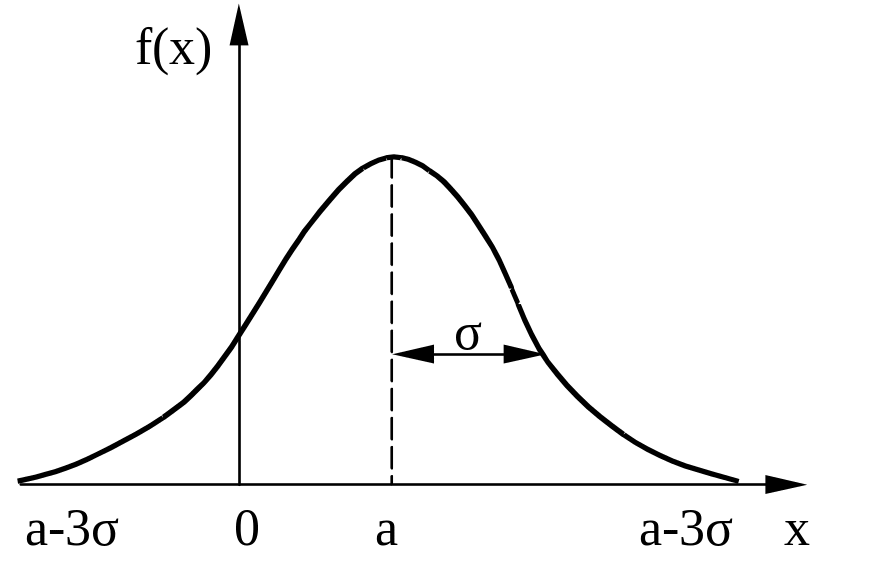
в) нормальное распределение;

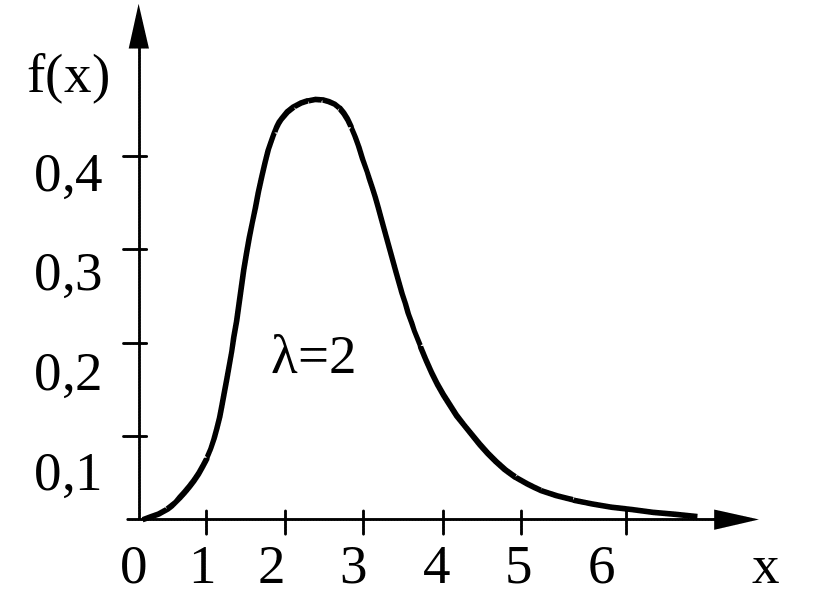
г) гамма-распределение

Рисунок 9.1 - Плотности распределения вероятностей

3. Случайные числа получаются на ЭВМ с помощью программ. При этом задаются некоторым числом ξ_о, из этого числа путем арифметических и логических операций получают следующее чис­ло ξ₁ затем преобразуют ξ₁ в ξ₂ и так далее. Так как числа ξ_о получаются в результате работы программы, эти чис­ла не являются истинно случайными, их называют псевдослучай­ными числами. Однако они могут успешно применяться в качест­ве случайных чисел, так как удовлетворяют требованиям слу­чайности, равномерности и имеют достаточно большую периодич­ность. Соответствующие программы для ЭВМ называются датчи­ками псевдослучайных чисел. Языки программирования высокого уровня, такие как Паскаль, Бейсик, Фортран, Си имеют соответ­ствующие стандартные функции, при обращении к которым гене­рируется псевдослучайное число из диапазона [0, 1] с равно­мерным законом распределения.

Моделирование случайных событий. Пусть необходимо смо­делировать случайное событие А, наступающее с заданной ве­роятностью Р.

В этом случае процедура моделирования состоит в генери­ровании случайного числа ξ с равномерным законом распреде­ления на отрезке [0, 1] и в сравнении этого числа с величиной г. Событие считается наступившим, если ξ ≤ Р (рисунок 9.2).

9.3 Моделирование случайных величин с заданным

законом рас­пределения

Реальные случайные величины очень редко описыва­ются равномерным распределением и подчиняются самым разнообразным законам распределения (нормальному, показательному, гамма-распределению и т.д.). В то же время моделирование на ЭВМ всех этих законов распределения, выполняется путем преоб­разования случайной величины, имеющей равномерное распределе­ние на отрезке [0, 1] .

Рисунок 9.2 - Структурная схема алгоритма моделирования

случайного события

Существует два основных пути такого преобразования слу­чайных чисел. Один из них, который может быть назван прямым, состоит в реализации некоторой операции над числом ξ, формирующей число η, имеющее заданный закон распределения. Другой путь основывается на моделировании условий соответст­вующей предельной теоремы теории вероятностей.

В первом случае используется так называемый метод об­ратной функции: если случайная величина Z имеет плотность распределения f(х), то распределение случайной величины

(9.1)

является равномерным на отрезке [0, 1].

Для моделирования случайных величин с законом распреде­ления f(х) представляет интерес обратная задача: зная за­кон распределения f(х) и имея случайные числа ξ_i , полу­чить случайные числа η_i, имеющие плотность распределения f(х). Это достигается путем разрешения относительно η_i. следующего уравнения

(9.2)

Если удается взять интеграл, то соотношение (9.2) может быть непосредственно использовано в моделирующих алгоритмах. Пусть требуется получить случайные числа η_i с показательным законом распределения (см. рисунок 9.1, б)

f(х) =λ · е^-λκ _, (х > 0) (9.3)

Тогда по методу обратной функции можно записать

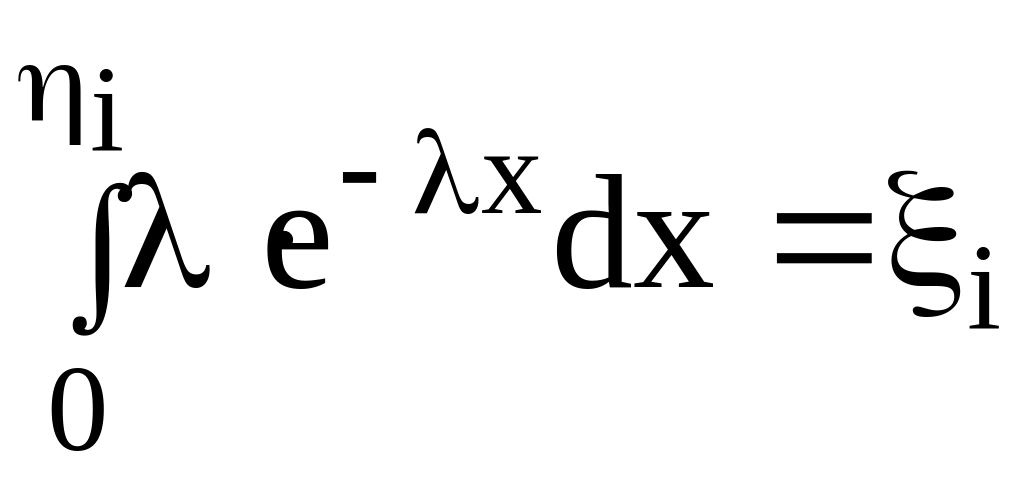. (9.4)

После вычисления интеграла имеем

(9.5)

Разрешая последнее уравнение относительно η_i. можно за­писать следующее соотношение для получения случайных чисел с показательным законом распределения

, (9.6)

Однако, для большинства законов распределения не удает­ся вычислить интеграл в уравнении (9.2) и, следовательно, вы­разить η_i через ξ_i. В этом случае прибегают к приближенным способам преобразования равномерного закона распределения в требуемый, при которых оказываются справедливыми соответст­вующие предельные теоремы.

Пусть требуется получить последовательность случайных чисел η_i, имеющих нормальное распределение (см. рисунок 9.1, в)

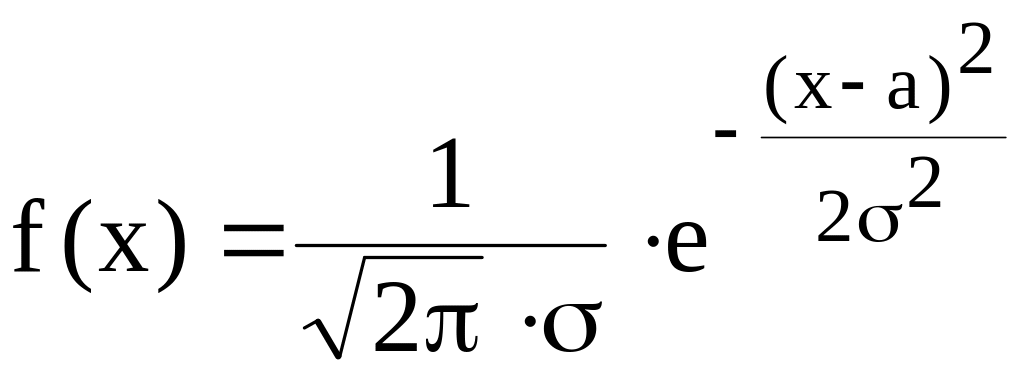, (9.7)

где а - математическое ожидание;

σ - среднеквадратическое отклонение.

Здесь можно воспользоваться центральной предельной тео­ремой теории вероятностей и построить случайные числа η_i в виде сумм последовательных случайных чисел, имеющих равно­мерное распределение на отрезке [0, 1] .

В частности, случайные числа, имеющие стандартизирован­ное нормальное распределение, у которого а = 0 и σ = 1, могут быть получены, например, по следующей зависимости

. (9.8)

Исходя из стандартизированного закона распределения, можно получить нормально распределенные случайные числа с произвольными значениями а и σ по формуле

. (9.9)

Алгоритм формирования n случайных чисел, имеющих нор­мальное распределение общего вида, приведен на рисунке 9.3.

Рисунок 9.3 - Структурная схема алгоритма моделирования