Содержание отчёта

Усиление сигналов

1. Принципиальная схема исследованных устройств.

2. Исходная и аппроксимированная сток–затворная характеристика полевого транзистора для соответствующего варианта.

3. Таблицы исходных, расчетных и экспериментальных данных.

4. Графики амплитудных характеристик ₁₂, а также осциллограммы исследованных процессов.

Умножение частоты

1. Принципиальная схема исследованных устройств.

2. Исходная и аппроксимированная сток–затворная характеристика полевого транзистора для соответствующего варианта.

3. Таблицы исходных, расчетных и экспериментальных данных.

4. Графики амплитудных характеристик ₁₂, а также осциллограммы и спектры исследованных процессов.

Контрольные вопросы

1. Какова роль полевого транзистора в схеме линейного усилителя?

2. Почему в качестве нагрузки в линейном усилителе применяются резистор, колебательный контур?

3. Как выбрать рабочую точку на характеристике усилительного элемента линейного усилителя?

4. Каковы преимущества нелинейных усилителей?

5. Какова связь между формой напряжения на входе и выходе нелинейного резонансного усилителя?

6. Какова роль избирательной нагрузки в схемах нелинейных усилителей?

7. Как выбрать рабочую точку на характеристике усилительного элемента нелинейного усилителя?

8. С какой целью применяются усилители?

9. Как выбрать оптимальный режим работы усилителя?

10. Как получить осциллограмму тока, протекающего через колебательный контур?

11. Что такое коэффициент гармоник?

12. Изобразить схему умножителя частоты. Пояснить принцип её работы.

13. С какой целью применяются умножители частоты?

14. Как выбрать оптимальный режим работы усилителя?

15. Как выбрать оптимальный режим работы умножителя частоты?

16. Какова роль нелинейного элемента в схеме умножителя частоты?

17. Какова роль избирательной нагрузки в схеме умножителя частоты?

18. Как получить осциллограмму тока, протекающего через колебательный контур?

19. Какое влияние оказывает выбор напряжения смещения на работу умножителя частоты?

20. Какое влияние и почему оказывает добротность контура нагрузки на качество работы умножителя частоты?

21. Что такое коэффициент гармоник?

ЛАБОРАТОРНАЯ РАБОТА №6

АМПЛИТУДНАЯ МОДУЛЯЦИЯ

Цель работы: исследование процесса амплитудной модуляции, получение статической модуляционной характеристики и выбор оптимального режима работы модулятора.

Краткие сведения из теории

Для сигналов с аналоговыми видами модуляции удобно использовать квазигармоническое представление:

,

где - огибающая процесса, - полная фаза .

Первое слагаемое здесь - текущая фаза, второе - девиация (отклонение) фазы. Учитывая, что и - суть медленно меняющиеся функции времени, за один период колебания с несущей частотой ₀, модулированный сигнал по форме представляет собой синусоиду. Этим и объясняется название "квазигармоническое", то есть почти синусоидальной формы.

Амплитудную модуляцию можно определить как вид модуляции, при котором девиация амплитуды пропорциональна информационному сигналу , а девиация фазы вырождается в начальную фазу .

, (6.1)

где К_АМ - коэффициент пропорциональности, характеризующий работу модулятора. Физический смысл этого коэффициента будет показан ниже.

Огибающая процесса может быть представлена как сумма постоянной составляющий (амплитуды несущего колебания) и девиации амплитуды:

(6.2)

Общая запись амплитудно-модулированного сигнала (АМ) имеет вид:

(6.3)

Для частного случая, тональной АМ:

; (  ₀ )

.

Величина ; вынося за скобку, получим:

Обозначим (глубина модуляции).

Окончательно для тональной модуляции:

(6.4)

Для модуляции сложным сигналом , а

здесь - частичная (парциальная) глубина модуляции; .

Временные диаграммы информационного сигнала и сигнала АМ представлены на рисунок 6.1.

Для получения спектра тонального АМ сигнала раскроем скобки выражения (6.4)

.

С пектрограммы исходного (информационного) сигнала и АМ сигнала показаны на рисунке 6.2.

Рисунок 6.1 Временные диаграммы тонального АМ сигнала

Спектр тонального АМ сигнала состоит из колебания несущей частоты и двух боковых, которые являются комбинационными частотами.

Итак, новыми колебаниями, возникающими в амплитудном модуляторе, являются комбинационные колебания второго порядка ₀  . Следовательно, наилучшей формой ВАХ нелинейного элемента в амплитудном модуляторе является квадратичная парабола: при . Если на вход нелинейного элемента подать бигармонический сигнал в спектре тока , кроме гармоник входных сигналов, образуются комбинационные колебания второго порядка :

(6.5)

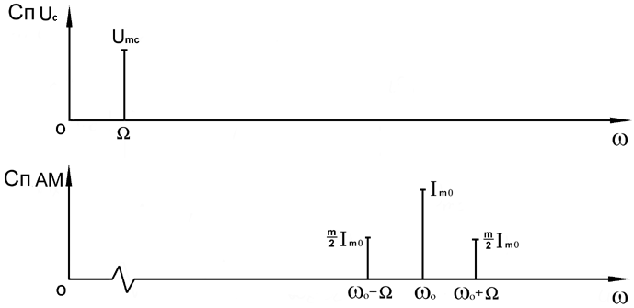
Рисунок 6.2 Спектр тонального АМ сигнала

Весь спектр тока показан на рисунке 6.3 Для выделения из спектра тока полезных компонентов сигнала (₀, ₀) необходимо применить полосовой фильтр с центральной частотой ₀ и полосой пропускания не уже 2.

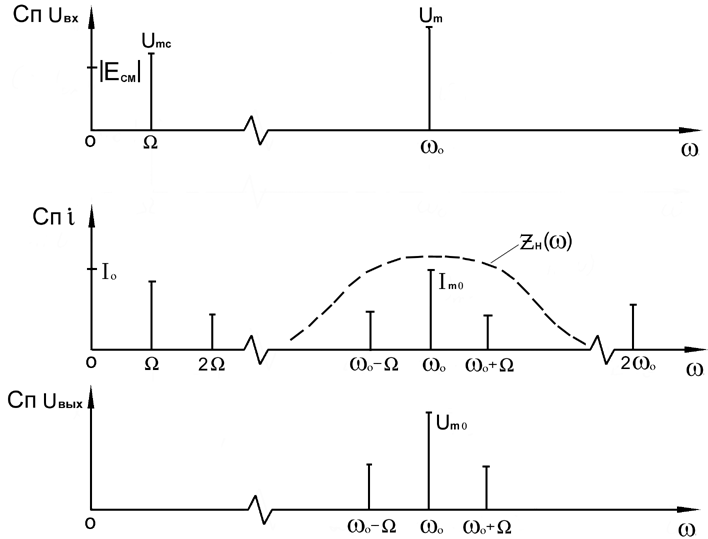
Рисунок 6.3 Спектры амплитудного модулятора

В простейшем варианте таким полосовым фильтром может быть параллельный контур с невысокой добротностью. (При высокой добротности контура в спектре выходного напряжения будут подавлены боковые частоты).

Для нахождения оптимального режима работы модулятора следует получить (расчетным или экспериментальным путем) статическую модуляционную характеристику (СМХ) при = const. Эта характеристика показывает возможности модулятора в изменении амплитуды сигнала.

Строятся несколько таких характеристик для разных амплитуд колебаний несущей частоты ( ) и из них выбирается та, которая имеет наибольший по протяженности линейный участок. Требование линейности СМХ вытекает из определения АМ. Тангенс угла наклона линейного участка СМХ (угла  на рисунке 6.4) является коэффициентом пропорциональности К_АМ. С помощью СМХ можно определить оптимальный режим амплитудного модулятора и его параметры:

- выбор оптимальной амплитуды сигнала несущей частоты (по максимальной протяженности линейного участка СМХ);

- границы линейного участка СМХ (средняя точка линейного участка соответствует оптимальному напряжению смещения и амплитуде несущего колебания (по вертикальной оси));

- максимальная амплитуда модулирующего сигнала - половина проекции линейного участка СМХ на горизонтальную ось графика;

- максимальная девиация амплитуды - половина проекции линейного участка СМХ на вертикальную ось;

- максимально достижимая глубина модуляции .

Рисунок 6.4 Статическая модуляционная характеристика