"Усиление сигналов. Умножение частоты"

Цель работы: исследование процессов усиления сигналов в линейном и нелинейном режимах. Изучение процесса умножения частоты. Получение оптимального режима.

Краткие сведения из теории усиление сигналов

В технике радиопередающих устройств широко применяются резонансные усилители мощности. Их отличительная черта – работа при больших амплитудах входных напряжений, что делает обязательным учёт нелинейного вида ВАХ активных элементов (транзисторов или ламп).

Рассмотрим транзисторный усилитель с нагрузкой в виде параллельного колебательного контура. На вход усилителя подано напряжение

U_вх(t) =U₀+U_{m вх} cost (5.1.1)

колебательный контур настроен на частоту сигнала: рез=.

Предположим, что характеристика i_к(U_бэ) транзистора аппроксимирована отрезками прямых. Ток в цепи коллектора имеет форму косинусоидальных импульсов с отсечкой. Эти импульсы обладают сложным спектральным составом, однако ведущую роль в работе устройства играет лишь первая гармоника тока, частота которой совпадает с резонансной частотой контура; сопротивление колебательной системы на частотах 2, 3 и т. д. столь мало, что высшие гармоники не дают вклада во входной сигнал.

Первая гармоника коллекторного тока создаёт на выходе полезное напряжение с амплитудой

U_mвых =(1R_рез =SR_резU_mвх) (5.1.2)

Используя эту формулу, можно записать выражение амплитуды гармонического сигнала на выходе резонансного усилителя при постепенной аппроксимации характеристики транзистора:

U_mвых =R_рез(a1U_mвх+3/4a3U³=5/8 a5U⁵_mвх +…). (5.1.3)

Важным параметром колебательной характеристики является ширина её линейного учёта, который определяет диапазон усиливаемых сигналов. Естественная причина , ограничивающая рост колебательной характеристики , состоит в следующем : при некотором критическом значении амплитуды входного сигнала U^kp_mвх колебательное напряжение на контуре становится близким по значению к напряжению источника питания Е_пит. Дальнейший рост амплитуды напряжения на контуре становится невозможным, поскольку при этом в некоторые моменты времени мгновенное значение напряжения на коллекторе транзистора становится малым. Как следствие, нормально запертый коллекторный переход открывается и цепь коллектор-база - источник сигнала - источник питания резко шунтирует колебательную систему усилителя.

Умножение частоты

Процесс умножения частоты сигнала - это получение n - ой гармоники входного моногармонического сигнала. Для того чтобы в спектре тока появились гармоники, саму форму этого сигнала надо сделать несинусоидальной, используя для этого нелинейный или параметрический элемент.

При нелинейном преобразовании моногармонического сигнала спектр тока нелинейного элемента содержит ряд гармоник (теоретически их число бесконечно), амплитуды которых могут быть рассчитаны, например, методом угла отсечки. Учитывая, что графики коэффициентов Берга имеют четко выраженные максимумы, можно определить оптимальные углы отсечки, соответствующие этим максимумам. Из графиков коэффициентов Берга () следует, что _опт=120⁰/n, где n - номер гармоники. Обращаем внимание на тот факт, что для других коэффициентов Берга формула _опт будет иная; например, для (), _опт=180⁰/n. При правильно выбранном угле отсечки амплитуда n - ой гармоники достигает максимума (оптимальный режим умножителя частоты).

_{mn max}= i_max (_опт). (5.2.1)

Для обеспечения этого максимума следует подобрать Е_см , если задана амплитуда входного сигнала U_m , либо наоборот, исходя из выражения

cos_опт = - (Е_см - )/ U_m. (5.2.2)

Для выделения нужной гармоники из сложного спектра тока можно использовать фильтр, в простейшем варианте - параллельный колебательный контур, настроенный на частоту нужной гармоники. Имея спектр тока и частотную характеристику контура z_н() (рисунок 5.1), можно легко рассчитать спектр выходного напряжения. Пусть, например, требуется выделить третью гармонику (n=3) входного сигнала с частотой ₀ . Амплитуды гармоник выходного напряжения могут быть рассчитаны на основании закона Ома. Так, для третьей гармоники сопротивление нагрузки (LC контура) будет максимальным (это частота резонанса в контуре) z_н(_р) = z_н(3₀) =  , где =L/C - характеристическое сопротивление , а - добротность. Амплитуда третьей гармоники напряжения:

U_m3 = I_m3 z_н (3₀) = I_m3 

Из курса ТЭЦ известно, что частотная зависимость модуля полного сопротивления параллельного колебательного контура:

(5.2.3)

Подставляя вместо  частоты соседних гармоник, определим z_н(₀), z_н(2₀) и т. д. Амплитуда любой гармоники напряжения на контуре:

U_mn = I_mnz_н(n₀)

В случае, когда добротность велика, спектр выходного напряжения будет состоять практически из одной третьей гармоники и форма выходного напряжения будет почти синусоидальной. Присутствие соседних гармоник обуславливает искажения формы выходного сигнала, которые могут быть количественно оценены коэффициентом гармоник:

К_Г= *100% (5.2.4)

Здесь Р_НЕЛ - суммарная мощность продуктов нелинейности (соседних гармоник c номерами 1,2,4,5 ..), а Р_ПОЛ - мощность полезной составляющей (третьей гармоники). Для рассматриваемого случая:

К_Г = 100%

Н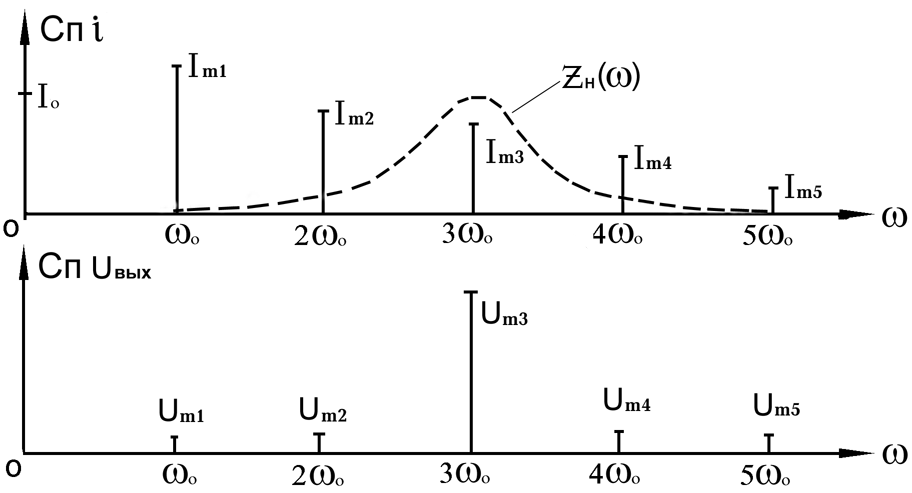 елинейное резонансное усиление можно рассматривать как частный случай умножения частоты на 1 (n=1). Рассмотрим КПД резонансного усилительного каскада

Рисунок 5.1 - Построение спектра выходного напряжения

где Р₁ - мощность первой гармоники сигнала (полезный сигнал); Р₀ - мощность, потребляемая от источника питания.

Для гармонического сигнала:

,

Для источника питания устройства:

При максимальной амплитуде U_m1 КПД также будет максимальным

;

учитывая, что при максимальной амплитуде сигнала U_m1  E - напряжению питания,

(5.2.5)

Для линейного режима работы ( =180⁰), (180⁰)= (180⁰)= ; ; т. е. 50% мощности источника питания переходит в тепло.

Для нелинейного режима работы   60⁰, .

Таким образом, усилительные каскады, работающие в нелинейном режиме, обладают большим КПД, что особенно важно в оконечных каскадах передающих устройств. Несмотря на то, что усилитель работает в нелинейном режиме и форма тока имеет вид косинусоидальных импульсов, выходное напряжение имеет практически синусоидальную (квазигармоническую) форму, т.к. контур в нагрузке каскада, настроенный на несущую частоту, подавляет все высшие гармоник.