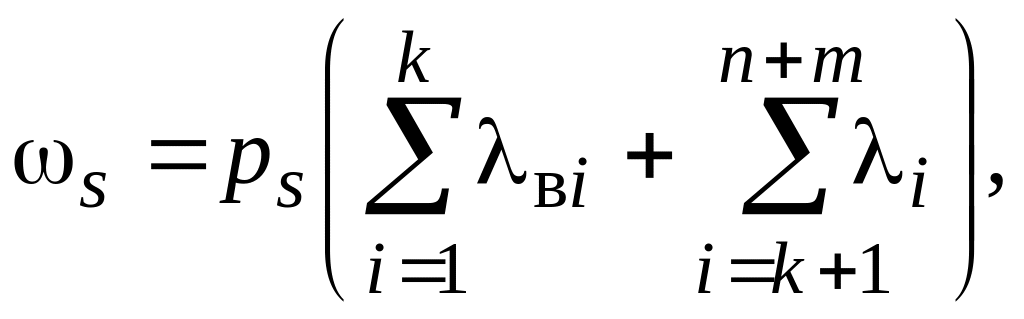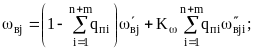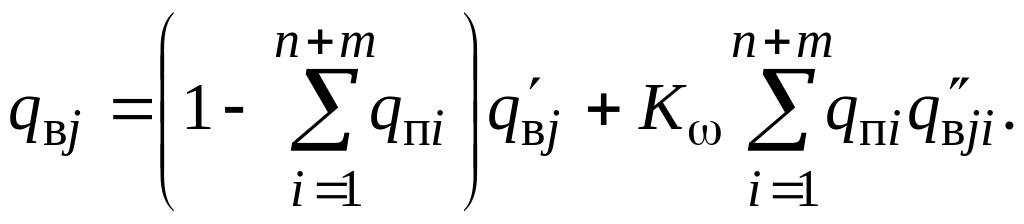3.4. Метод прямого обчислення показників структурної надійності схем електричних мереж

Розглянуті структурні аналітичні методи аналізу надійності схем ЕМ передбачають складання та перетворення еквівалентних розрахункових схем надійності. Ці схеми складають і перетворюють для кожного споживача ЕМ окремо. Будь-яка зміна схеми ЕМ (наприклад, під час переходу мережі в режим мінімального навантаження) вимагає нового складання та перетворення еквівалетних розрахункових схем надійності, тобто виконання нових розрахунків. Ці недоліки істотно ускладнюють програмування задач аналізу структурної надійності ЕМ та користування розробленими програмами.

Метод прямого обчислення показників структурної надійності ЕМ не передбачає складання та перетворення будь-яких розрахункових схем. Його розрахунковий процес будується на базі методу простору станів і формується за допомогою матриці, яка відображає повну структуру мережі та фіксує всі можливі зв’язки споживачів з джерелами живлення. Такою матрицею може бути перша матриця інциденцій (матриця сполучень), але з її допомогою важко прослідковувати зв’язки споживачів з джерелами живлення, що ускладнює програмування задачі аналізу надійності. Доцільніше використовувати матрицю, рядки та стовпці якої підпорядковані вузлам схеми мережі. Таку матрицю назвемо матрицею вузлів і позначимо її символом .

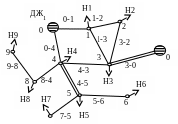
На рис. 3.12,а зображена схема електричної мережі, в якій позначено джерела живлення (ДЖ₁, ДЖ₂), вузли схеми, від яких живляться споживачі Нj та вітки, що з’єднують вузли. Вузли пронумеровані числами натурального ряду, а вітки – подвійними числами, які відповідають номерам з’єднуваних вузлів. Джерела живлення мають необмежену потужність, абсолютну надійність і тому об’єднані в один нульовий вузол. Вузли мережі враховують системи шин та інші елементи підстанцій, відмови яких спричиняють перерви електропостачання споживачів. Вітки схеми враховують ЛЕП та елементи підстанцій, відмови яких призводять до втрати зв’язків між вузлами.

0 1 2 3 4 5 6 7 8 9 1 1 1 0 1 1 1 1 1 1 2 1 1 1 1 3 1 1 1 1 4 1 1 1 5 1 6 1 7 1 1 8 1 9

а б

Рис. 3.12. Схема електричної мережі (а) та її матриця вузлів (б)

Схемі мережі (рис. 3.12,а) відповідає деяка матриця (рис. 3.12,б), заповнена одиницями, які ставлять на перетині рядка і стовпця та стовпця і рядка в разі наявності між двома відповідними вузлами з’єднувальної вітки. Наприклад, наявність вітки між четвертим і третім вузлами відображена двома одиницями на перетинах четвертого рядка і третього стовпця та третього рядка і четвертого стовпця. За цією матрицею легко прослідковують зв’язки споживачів з джерелами живлення. Наприклад, споживач Н₅, що безпосередньо зв’язаний з п’ятим вузлом, через відповідні вітки (одиниці в рядках і стовпцях) має зв’язок з вузлами 4, 6, 7, один з яких (четвертий) виходить на нульовий вузол, тобто на джерело живлення.

У поточні моменти часу деякі вітки та вузли мережі можуть переходити в неробочий стан і порушувати зв’язки споживачів з джерелами живлення, викликаючи цим перерви електропостачання. Відмову вітки можна зафіксувати в матриці викресленням двох одиниць, які належать з’єднуваним цією віткою вузлам. Відмову вузла можна зафіксувати викресленням пар одиниць усіх віток, які належать вказаному вузлові, оскільки відмова вузла супроводжується втратою його зв’язків з усіма іншими вузлами. При цьому в рядку і стовпці даного вузла зникають всі одиниці, що є ознакою втрати живлення відповідним споживачем. Відмови деяких вузлів можуть мати складніші наслідки. Наприклад, відмова вузла 4 супроводжується зниканням одиниць у четвертому рядку та стовпці, тобто знеструмленням четвертого споживача, а також посередньою втратою зв’язків з джерелами живлення споживачами Н₅, Н₆, Н₇, Н₈, Н₉. Можливі поєднання відмов віток, вузлів та віток і вузлів. Накриклад, якщо одночасно відмовлять вітки 1-2 і 3-2, то всі одиниці зникнуть у другому рядку та стовпці, тобто втратить живлення споживач Н₂.

Матриця відіграє в розробленому методі ключову роль. Вона дає змогу автоматизувати перебір станів електричної мережі та формалізувати за рахунок такої автоматизації відомий метод простору станів. Такі можливості цієї матриці зумовлені тим, що з її допомогою для кожного стану електричної мережі (відмова будь-яких вузлів, віток та їх комбінацій) за допомогою реалізованого на комп’ютері алгоритму контролюють зв’язки споживачів з джерелами живлення.

У методі простору станів розглядають усі можливі елементарні стани мережі, зумовлені станами (робочий, неробочий) її віток і вузлів. Якщо кількість віток становить n, а вузлів m, то кількість елементарних станів дорівнює . Для кожного s-го елементарного стану можна встановити ймовірність і частоту його виникання. Припускаючи незалежність відмов елементів мережі та враховуючи мале значення ймовірності відмови елемента мережі порівняно з імовірністю його нормальної роботи, ймовірність можна розрахувати наближено за теоремою множення ймовірностей. Якщо в s-му стані мережі k віток та вузлів відмовили, а n+m-k працюють, то

(3.37)

Частоту , рік^-1 виникання s-го елементарного стану розраховують як добуток імовірності на суму інтенсивностей переходів з s-го стану в усі інші (2.43). В нашому випадку

(3.38)

де – відповідно інтенсивність відновлення та інтенсивність відмови і-го елемента мережі, рік^-1.

Величини , розраховують за відомими статистичними показниками надійності елементів мережі

(3.39)

де – статистична частота відмов і-го елемента, рік^-1; – середньостатистичний час вимушеного простою і-го елемента, годин.

Розраховуючи для кожного s-го стану величини і фіксуючи за допомогою матриці , які споживачі в даному стані втрачали живлення, можна встановити ймовірність і частоту вимушеного припинення електропостачання кожного j-го споживача в усій сукупності елементарних станів мережі

(3.40)

Отримані для всієї сукупності елементарних станів величини , є фактично показниками надійності електропостачання кожного j-го споживача. Будучи визначеними для всіх споживачів, ці величини характеризують структурну надійність схеми електричної мережі та служать основою для встановлення інших її показників.

Загальна кількість елементарних станів, які теоретично підлягають аналізові, надзвичайно велика. Проте аналізувати всі стани потреби немає, оскільки значна їх частина має дуже низьку ймовірність виникання. Добуток k значень у формулі (3.37) практично перетворюється в нуль для . Отже, враховувати потрібно тільки стани, зумовлені відмовами елементів мережі по одному , по два , та по три .

Використання матриці забезпечує впорядкований та автоматизований перебір станів електричної мережі. Стани відмов віток і вузлів мережі по одному фіксують в порядку зростання їх номерів відповідним усуванням одиниць в рядках і стовпцях матриці за розглянутим вище способом. Після переходу в кожен новий х-й стан розраховують величини і додають їх до значень , усіх споживачів, які втратили живлення в х-му стані. Розрахунок повторюють разів і виконують за таким алгоритмом:

(3.41)

для .

Під час перебору станів, зумовлених відмовами двох елементів x та y, розрахунок повторюють до вичерпання поєднань по два і виконують за таким алгоритмом:

(3.42)

для .

Під час перебору станів мережі, зумовлених відмовами трьох елементів x, y, z розрахунок повторюють до вичерпання поєднань по три і виконують за таким алгоритмом

(3.43)

для .

Перебір станів у наведеному порядку дозволяє встановити два основні показники надійності електропостачання кожного окремого споживача, коли планові ремонти елементів мережі не враховують:

- частота вимушених перерв електропостачання, рік^-1,

(3.44)

- імовірність вимушеної перерви електропостачання, відн. од.,

(3.45)

Щоб врахувати планові ремонти, розрахунки за наведеними формулами необхідно повторити разів. Крім уже встановлених значень , отриманих для повної схеми, потрібно розрахувати значень , отриманих для схеми без виведеного в ремонт і-го елемента , імовірність перебування якого в ремонтному стані становить .

Основні показники надійності електропостачання кожного окремого споживача з урахуванням планових ремонтів елементів мережі розраховують за формулою повної імовірності:

- частота вимушених перерв електропостачання, рік^-1,

(3.46)

- імовірність вимушеної перерви електропостачання, відн. од.,

(3.47)

Отримані показники дозволяють за формулами (3.1, 3.2, 3.10, 3.11) встановити решту показників надійності кожного окремого споживача та мережі в цілому.

Підсумовуючи, відзначимо, що наведені обчислювальні процедури характеризуються високим ступенем формалізації. Це зручно для програмування, підготовки вхідної інформації та аналізу результатів комп’ютерних розрахунків.