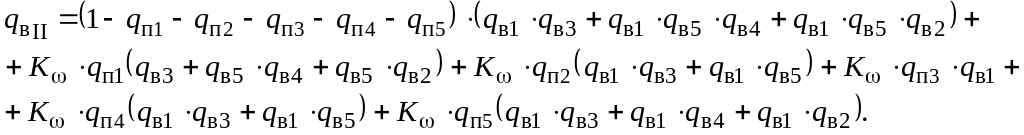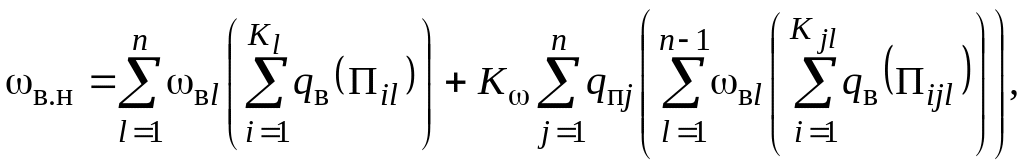3.3. Аналіз структурної надійності складних схем електричних мереж

Для аналізу надійності складних схем ЕМ найчастіше застосовують структурні методи, які дозволяють складні структури звести до послідовно-паралельних чи паралельно-послідовних і встановити показники надійності електропостачання споживачів подібно до того, як вони встановлювалися для електроустановок під час побудови моделей надійності на базі основних теорем теорії ймовірностей за умови, що функції надійності Р_і(t) поставлена у відповідність імовірність р_і робочого стану, а функції ненадійності Q_і(t) - імовірність q_і неробочого стану кожного елемента схеми.

Структуру схеми ЕМ можна перетворити, дослідивши її граф. Методи структурного аналізу дозволяють виявити всі шляхи між двома будь-якими вершинами графа. З погляду аналізу надійності ЕМ інтерес являють тільки шляхи між джерелами живлення тапоживачем.

Шлях схеми ЕМ - це та мінімальна сукупність її елементів, робочий стан яких забезпечує передачу електроенергії від джерела живлення до споживача.

На рис. 3.9,б зображені шляхи схеми рис. 3.9,а, які в сукупності утворюють еквівалентну послідовно-паралельну схему.

Рис. 3.9. Схема мережі (а) та її еквівалентні розрахункові схеми надійності (б,в)

Еквівалентну паралельно-послідовну схему можна отримати, виявивши мінімальні перерізи мережі.

Мінімальний переріз схеми ЕМ - це та мінімальна сукупність її елементів, одночасний неробочий стан яких спричинює перерву електропостачання споживача.

На рис. 3.9,в зображені мінімальні перерізи схеми рис. 3.9,а. Переріз 1, 5, 2, 6 не мінімальний, бо має зайві елементи. Такі перерізи не розглядаються.

Незважаючи на те, що методи структурного аналізу дозволяють виявляти шляхи та формувати еквівалентну послідовно-паралельну схему, надійність ЕМ розраховують переважно за схемою мінімальних перерізів через її високу інформативність. Ця схема чітко показує вплив на рівень надійності електропостачання споживачів окремих елементів схеми ЕМ та їх поєднань. Схему мінімальних перерізів можна отримати двома різними способами: зі схеми шляхів; безпосередньо зі схеми ЕМ. За першим способом спочатку формують матрицю шляхів , підпорядковуючи стовпці елементам послідовно-паралельної схеми, а рядки - її віткам, тобто шляхам. Для схеми рис. 3.9,б ця матриця має такий вигляд

1 2 3 4 5 6 1 1 1 ш1 1 1 1 ш2. 1 1 1 1 ш3 1 1 1 1 ш4

Якщо деякий елемент, наприклад 6, входить в усі шляхи, то він утворює одноелементний переріз, бо відмова цього елемента обриває всі зв’язки споживача з джерелом живлення. Якщо в кожному зі шляхів перебуває хоча б один з двох елементів, наприклад 1 і 3, то вони утворюють двоелементний переріз, бо їх одночасний неробочий стан також призводить до обриву всіх зв’язків споживача з джерелом живлення.

Формалізувати пошук мінімальних перерізів дозволяє операція логічного додавання. Мінімальні перерізи утворюють ті стовпці матриці , у результаті логічного додавання яких формується одиничний стовпець. Перед виконанням операцій логічного додавання стовпців з матриці слід усунути всі одиничні стовпці, бо вони утворюють одноелементні перерізи. Двоелементні перерізи можна виявити шляхом логічного додавання всіх стовпців попарно, а триелементні - шляхом логічного додавання всіх стовпців по три і т.д. Поєднання стовпців, які утворили мінімальний переріз в подальших операціях додавання брати участі не повинні, бо вони будуть формувати немінімальні перерізи.

За другим способом аналізують граф неперетвореної схеми надійності мережі. Такий граф має один вхід А (джерело) і один вихід Е (споживач), як показано на рис. 3.10,а.

Нехай задано граф, що містить m ребер і М вершин. Розірвемо ребра графа так, щоб частина вершин N була приєднана тільки до входу графа, а решта M-N вершин - до виходу (рис. 3.10,б). Розрив порушує зв’язок між входом і виходом графа й утворює дві структури, що називаються деревами: N-дерево (тобто дерево, що містить N вершин) і (M-N)-дерево. При цьому обірвані ребра утворюють мінімальний переріз (на рис. 3.10,б - ребра 3, 5, 6).

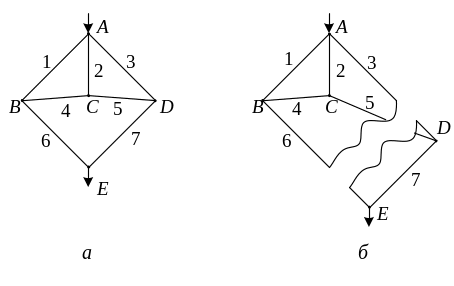
Рис. 3.10. Граф електричної мережі

Таким чином, пошук мінімальних перерізів зводиться до побудови можливих дерев графа. Для цього до однієї з вершин графа ( входу чи виходу) послідовно приєднуються одна за одною вершини, безпосередньо зв’язані з попереднім деревом.

Алгоритм визначення мінімальних перерізів такий.

1. Складають матрицю безпосередніх зв’язків вершин – ребер графа.

2. Складають масив N-дерев графа послідовним приєднанням до N_i-дерева вершин, безпосередньо зв’язаних з однією із вершин, що вже належать до N_i-1-дерева.

3. Для кожного N_i-дерева обирають перерізи.

4. Складають масив перерізів, з якого вибирають мінімальні.

Проаналізуємо визначення мінімальних перерізів для структури (див. рис. 3.10,а). 

1. Складаємо матрицю безпосередніх зв’язків вершин і ребер графа. Наприклад, вершина А безпосередньо зв’язана з ребрами 1, 2, 3, вершина В - з ребрами 1, 4, 6 тощо. Матриця зв’язків має вигляд

			А	В	С	D	Е
			123	146	245	357	67

2. Складаємо масив N-дерев. Перше N₁-дерево – це вершина А. Потім до неї по черзі приєднують три суміжні вершини В, С, D і утворюються наступні N₂-дерева АВ, АС, АD. Далі до дерева АВ приєднують вершину D, оскільки вона зв’язана з вершиною А. Одержимо N₃-дерево АВD. Крім того, до N₂-дерева приєднують вершину С тощо, поки не будуть розглянуті всі вершини, за винятком Е - виходу графа (якщо вершину Е приєднати до N-дерева, то утвориться зв’язана структура). Отже, масив N-дерев графа має вигляд

А, АВ, АС, АD , АВС, АВD , АСD , АВСD.

3. Для кожного N_і-дерева визначають перерізи. З матриці зв’язків вершини-ребра у стовпчик виписують всі ребра, безпосередньо зв’язані з вершинами N-дерев (табл. 3.4). Ребра, що належать сукупності ребер N_і-дерева парне число раз, виключають (у табл. 3.4 вони перекреслені), а ребра, що залишилися, виписують у нижній рядок табл. 3.4.

Таблиця 3.4

Визначення перерізів схеми мережі

N-дерева	А	АВ	АС	АD	АВС	АВD	АСD	АВСD
	123	123	123	123	123	123	123	123
Ребра		146	245	357	146	146	245	146
					245	357	357	245
								357
Перерізи	123	2346	1345	1257	356	24567	147	67

4. Вибираємо з множини одержаних перерізів мінімальні. Для цього всі перерізи подають в порядку зростання числа елементів і уточнюють, чи не містяться в перерізах з більшим числом елементів перерізи з меншим числом елементів. Так, переріз 24567, утворений деревом АВD, містить переріз 67, утворений деревом АВСD. Тому переріз 24567 виключають. Перерізи 67, 123, 147, 356, 1257, 1345, 2346 є мінімальними.

Слід зауважити, що широковживаний термін «мінімальні перерізи» неточний. Аналіз обидвох способів отримання мінімальних перерізів свідчить, що йдеться фактично про безнадлишкові перерізи. Тому доцільно було б замість терміна «мінімальні перерізи» вживати термін «безнадлишкові перерізи».

Усі елементи ЕМ високонадійні . Це означає, що ймовірність збігу неробочих станів чотирьох і більше елементів близька до нуля. Фактично для схем ЕМ обов’язковому врахуванню підлягають одно- та двоелементні перерізи. Врахування триелементних перерізів змінює результати обчислення показників надійності в межах одного-трьох відсотків.

Алгоритм розрахунку показників надійності електропостачання споживача будується на базі основних теорем теорії ймовірностей і тому досить простий за структурою. Імовірність перерви електропостачання споживача (ймовірність неробочого стану мережі відносно вузла навантаження q_в.н) в умовах нормальної роботи ЕМ, коли відсутні планові вимикання її елементів, розраховують за формулою

(3.29)

де k - загальна кількість мінімальних перерізів схеми; - імовірність неробочого стану і-го мінімального перерізу; k₁, k₂, k₃ - кількість одно-, дво- та триелементних перерізів; - ймовірність вимушеного простою елемента і-го одноелементного перерізу; - імовірності вимушеного простою l-го та r-го елемента і-го двоелементного перерізу; - імовірності вимушеного простою l-го, r-го та s-го елемента і-го триелементного перерізу.

У загальному випадку, коли враховують планові (намірені) вимикання елементів мережі, ймовірність обчислюють за формулою

(3.30)

де n - загальне число елементів розрахункової схеми надійності; - імовірність планового простою j-го елемента розрахункової схеми; - число мінімальних перерізів розрахункової схеми після виключення з неї j-го елемента; - імовірність неробочого стану і-го мінімального перерізу з виключеним j-м елементом.

Вираз (3.30) отримано на основі формули повної імовірності, коли як подію розглядають перерву електропостачання споживача, а як гіпотези - нормальний і всі ремонтні стани мережі.

Приклад 3.4. Обчислити ймовірність перерви електропостачання споживача ІІ мережі рис. 3.11,а, утвореної повітряними лініями 110 кВ на залізобетонних опорах довжиною l₁=l₂=30 км; l₃=l₄=40 км; l₅ =50 км.

Розв'язання. За даними табл. 3.1 і формулами (3.2), (3.4), (3.8) обчислюємо значення ймовірностей вимушеного та планового простоїв усіх п'яти ліній:

Рис. 3.11. Схема мережі (а) та її мінімальні перерізи в нормальному (б) та ремонтних режимах (в, г, д, е, є)

На рис. 3.11,б зображено еквівалентну паралельно-послідовну схему для випадку нормального режиму роботи мережі, а на рис. 3.11,в,г,д,е,є - для випадків ремонту відповідно 1-ої, 2-ої, 3-ої, 4-ої, 5-ої лінії. Мінімальні перерізи ремонтних схем можна отримати безпосередньо зі схеми рис. 3.11,а або з еквівалетної схеми нормального режиму після усунення з неї елемента, що ремонтується, та виниклих немінімальних перерізів.

Імовірність перерви електропостачання споживача ІІ обчислюємо за формулою (3.30)

Підставивши розраховані значення імовірностей вимушеного та планового простоїв елементів схеми мережі та прийнявши К_ω = 0,5, отримаємо q_вII=5,84×10^-6.

Частота перерв електропостачання споживача у складних схемах розраховується на основі виразу, який випливає з обгрунтованої в § 3.2 формули (3.18). Перепишемо її у вигляді

(3.31)

Формула складається з двох частин. У першій частині визначається частота накладань відмов на відмови, у другій - відмов на планові ремонти. Процедуру обчислень за цією формулою можна перенести на випадок складної схеми. У складній схемі для визначення частоти перерв електропостачання споживача необхідно взяти суму добутків частоти відмов кожного елемента на ймовірність неробочого стану схеми без цього елемента, а також суму добутків імовірностей планового простою кожного елемента на частоту відмов схеми без цього елемента. У результаті отримуємо

(3.32)

де - число мінімальних перерізів схеми без l-го елемента; - імовірність неробочого стану і-го мінімального перерізу схеми без l-го елемента; - число мінімальних перерізів схеми без j-го та l-го елементів; - імовірність неробочого стану і-го мінімального перерізу схеми без j-го та l-го елементів.

Під час проектних розрахунків, коли невідомий графік виведення елементів мережі в ремонт, певну проблему являє собою врахування планових простоїв, бо у складних схемах намірені вимикання елементів часто суміщають. Якщо такого суміщення не враховувати, то може виникнути ситуація, коли сума величин q_пj перевищить одиницю і результати обчислень показників надійності будуть неправильними. Тому кожен раз необхідно складати перелік станів намірених вимикань і добиватися дотримання умови

(3.33)

Якщо в схемі наявні послідовно працюючі елементи (блоки трансформатор-вимикачі-роз'єднувачі тощо), намірені вимикання яких суміщають, то ймовірність планового простою приписують одному елементові групи і розраховують як

(3.34)

Записана формула отримана з (3.17), де ідентифіковано всі величини та пояснено порядок обчислень.

Середньорічний недовідпуск електроенергії та середньорічні збитки по мережі в цілому розраховують за формулами, аналогічними (3.11).

(3.35)

Недовідпуск електроенергії споживачам мережі протягом деякого періоду часу Т, меншого від року, визначають як

(3.36)

де - середнє за проміжок часу Т значення потужності і-го споживача.

Величина недовідпуску електроенергії споживачам мережі за проміжок часу Т (місяць, тиждень, доба, година) може слугувати критерієм прийняття рішень щодо поточної зміни схеми мережі під час планування режимів та оперативного керування ними.