
- •Теоретичні відомості
- •Завдання.
- •Щоб одержати початковий наближений розв'язок задачі, будемо вважати, що функція по горизонталях області розподілена рівномірно.
- •Робота 2
- •Завдання.
- •1. Використовуючи симетрію заданих початкових умов, побудуємо розв'язок тільки у чверті. Візьмемо крок і складемо таблицю значень і :
- •Робота 3
- •Завдання.
- •Робота 4
- •Завдання.
Робота 2
Завдання.
Використовуючи метод сіток, знайти
розв'язок диференціального рівняння
Лапласа
з заданими початковими умовами; крок
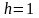 .
Уточнення розв'язку зробити до сотих
частин за допомогою процесу Лібмана.
.
Уточнення розв'язку зробити до сотих
частин за допомогою процесу Лібмана.
№1 |
|
|
№2 |
|
|
№3 |
|
|
№4 |
|
|
№5 |
|
. |
№6 |
|
. |
№7 |
(Г), |
. |
№8 |
(Г), |
. |
№9 |
|
. |
№10 |
(Г), |
. |
№11 |
(Г), |
|
№12 |
(Г), |
|
№13 |
(Г), |
|
№14 |
(Г), |
|
№15 |
|
. |
№16 |
(Г), |
. |
№17 |
|
|
№18 |
(Г), |
|
№19 |
(Г), |
. |
№20 |
|
. |
№21 |
|
|
№22 |
|
|
№23 |
|
. |
№24 |
(Г), |
. |
№25 |
(Г), |
|
№26 |
(Г), |
|
№27 |
(Г), |
. |
№28 |
|
. |
№29 |
(Г), |
. |
№30 |
|
. |
Зразок виконання завдання (Г); . |
1. Використовуючи симетрію заданих початкових умов, побудуємо розв'язок тільки у чверті. Візьмемо крок і складемо таблицю значень і :
-
0
1
2
3
4
3
2,90
2,60
1,98
0
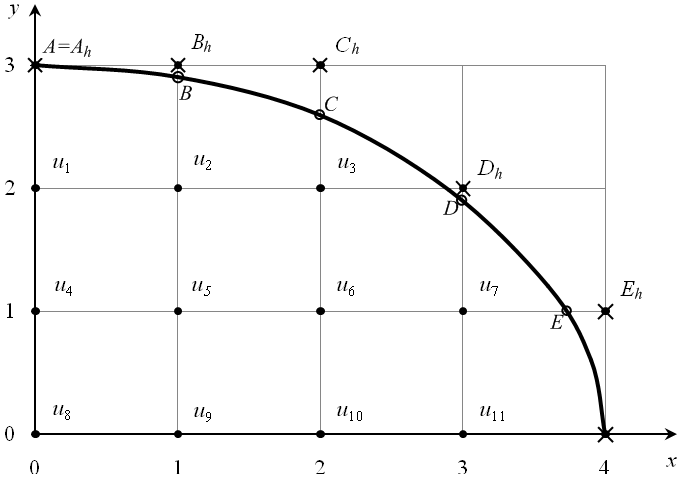
Рис.7
На рисунку хрестиками позначено граничні
вузли, кружечками – внутрішні, точки
 - точки, які належать межі Г області
.
- точки, які належать межі Г області
.
Обчислимо значення функції на межі:
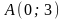 ;
;
 ,
,
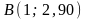 ;
;
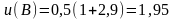 ,
,
 ;
;
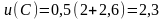 ,
,
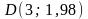 ;
;
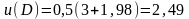 ,
,
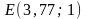 ;
;
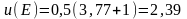 ,
,
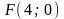 ;
;
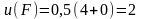 .
.
Для визначення початкових значень функцій у внутрішніх точках складемо систему рівнянь, що містять ці значення. Кожне рівняння отримується прирівнюванням значення функції у внутрішній точці середньому арифметичному чотирьох значень функції в сусідніх точках:
 ,
,
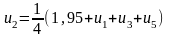 ,
,
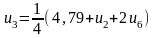 ,
,
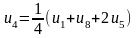 ,
,
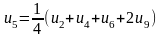 ,
,
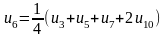 ,
,
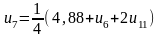 ,
,
 ,
,
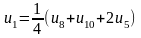 ,
,
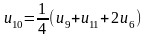 ,
,
 .
.
Розв'язавши цю систему, одержимо
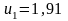 ,
,
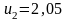 ,
,
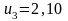 ,
,
 ,
,
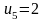 ,
,
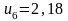 ,
,
 ,
,
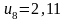 ,
,
 ,
,
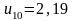 ,
,
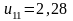 .
.
Знайдені значення функції дозволяють скласти шаблон №1, у якому внутрішні значення відповідають знайденим, а граничні одержуються в результаті уточнення попередніх граничних значень за формулою лінійної інтерполяції
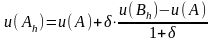 ,
,
де – вузлова гранична точка; – найближча до точка, що лежить на межі; – найближча до вузлова точка, що лежить всередині області; – відстань між точками і , узята зі знаком плюс, якщо точка лежить всередині області, і зі знаком мінус, якщо вона лежить поза областю.
У даному прикладі маємо:
 ;
;
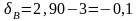 ;
;
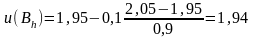 ;
;
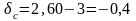 ;
;
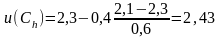 ;
;
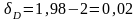 ;
;
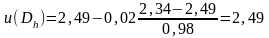 ;
;
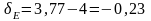 ;
;
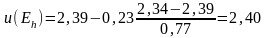 ;
;
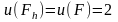 .
.
№1. |
|
|
|
|
1,5 |
1,94 |
2,43 |
|
|
1,91 |
2,05 |
2,10 |
2,49 |
|
2,05 |
2,11 |
2,18 |
2,34 |
2,40 |
2,11 |
2,13 |
2,19 |
2,28 |
2 |
Процес Лібмана полягає в уточненні значень, що входять у шаблон №1. Кожний наступний шаблон одержується з попереднього наступним чином: значення функції у внутрішніх точках дорівнюють середньому арифметичному чотирьох сусідніх значень попереднього шаблона, а значення функції в граничних точках знаходяться за формулою лінійної інтерполяції, яка вже використовувалася при одержанні шаблона №1. Ці уточнення проводяться до тих пір, поки два послідовних шаблони не збіжаться з заданою точністю. У результаті обчислень одержимо наступну послідовність шаблонів:
№2. |
|
|
|
|
|
№3. |
|
|
|
|
1,5 |
1,94 |
2,31 |
|
|
|
1,5 |
1,94 |
2,33 |
|
|
1,91 |
2,02 |
2,29 |
2,49 |
|
|
1,90 |
2,06 |
2,25 |
2,49 |
|
2,06 |
2,10 |
2,18 |
2,34 |
2,40 |
|
2,05 |
2,10 |
2,23 |
2,32 |
2,41 |
2,09 |
2,13 |
2,19 |
2,22 |
2 |
|
2,10 |
2,12 |
2,18 |
2,22 |
2 |
№4. |
|
|
|
|
|
№5. |
|
|
|
|
1,5 |
1,94 |
2,31 |
|
|
|
1,5 |
1,94 |
2,33 |
|
|
1,92 |
2,05 |
2,28 |
2,49 |
|
|
1,91 |
2,06 |
2,26 |
2,49 |
|
2,05 |
2,12 |
2,21 |
2,34 |
2,40 |
|
2,06 |
2,11 |
2,23 |
2,33 |
2,41 |
2,09 |
2,12 |
2,20 |
2,20 |
2 |
|
2,09 |
2,14 |
2,19 |
2,22 |
2 |
№6. |
|
|
|
|
|
№7. |
|
|
|
|
1,5 |
1,94 |
2,31 |
|
|
|
1,5 |
1,94 |
2,32 |
|
|
1,92 |
2,06 |
2,28 |
2,49 |
|
|
1,92 |
2,06 |
2,27 |
2,49 |
|
2,06 |
2,12 |
2,22 |
2,34 |
2,40 |
|
2,06 |
2,12 |
2,23 |
2,33 |
2,41 |
2,10 |
2,13 |
2,20 |
2,21 |
2 |
|
2,10 |
2,20 |
2,22 |
2,22 |
2 |
№8. |
|
|
|
|
|
|
|
|
|
|
1,5 |
1,94 |
2,32 |
|
|
|
|
|
|
|
|
1,92 |
2,06 |
2,27 |
2,49 |
|
|
|
|
|
|
|
2,06 |
2,12 |
2,23 |
2,33 |
2,41 |
|
|
|
|
|
|
2,10 |
2,13 |
2,20 |
2,22 |
2 |
|
|
|
|
|
|
Шаблон №8 є відповіддю.

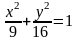 (Г),
(Г), .
.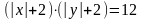 (Г),
(Г),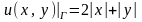 .
.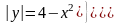 (Г),
(Г),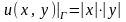 .
.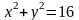 (Г),
(Г),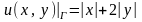 .
. (Г),
(Г),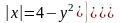 (Г),
(Г), (Г),
(Г), .
. .
.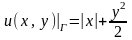 .
.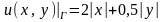 .
.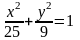 (Г),
(Г),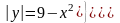 (Г),
(Г), .
.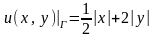 .
.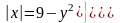 (Г),
(Г), (Г),
(Г),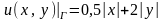 .
.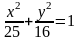 (Г),
(Г),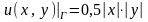 .
.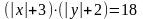 (Г),
(Г),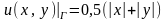 .
.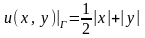 .
.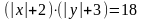 (Г),
(Г),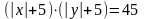 (Г),
(Г),