7. Наближені методи розв'язування диференціальних рівнянь з частинними похідними

Теоретичні відомості

1⁰. Рівняння Лапласа .

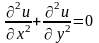І Схема для заміни рівняння Лапласа скінченно-різницевим рівнянням:

.

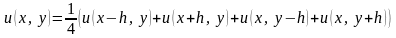ІІ Схема для заміни рівняння Лапласа скінченно-різницевим рівнянням:

.

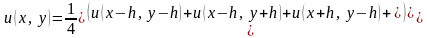а) Задача Дирихлє для рівняння Лапласа полягає в знаходженні функці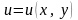ї , що задовольняє даному рівнянню всередині деякої області 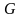, а на межі цієї області Г – умові 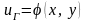, де 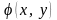- задана неперервна функція.

Метод сіток полягає в тому, що вибирають крок 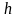і будують сітку , яка покриває дану область .

Виділивши граничні та внутрішні вузли, замінюють дане рівняння у внутрішніх точках скінченно-різницевим рівнянням, використовуючи схему І або ІІ, а в граничних точках значення 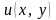функції знаходять із додаткової умови. Розв’язавши одержану систему, складають таблицю значень шуканої функції.

б) Процес усереднення Лібмана ззастосовується при розв’язуванні задачі Дирихлє для рівняння Лапласа. При цьому використовуються формули:

для внутрішніх точок

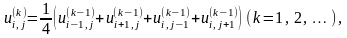
де - початкові значення у внутрішніх точках, взяті із розв’язку системи чи довільно;

для вузлових граничних точок

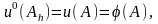
де 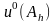- початкові значення функції в точці , 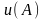- значення функції в точці 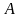, що лежить на межі;

,

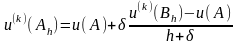де 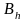- найближча до вузлова точка, що лежить в середині області ; - відстань між точками та , взяте зі знаком плюс, якщо - внутрішня точка області , і зі знаком мінус, якщо - зовнішня точка області .

2⁰. Змішана задача для рівняння теплопровідності 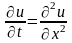полягає у визначенні функції , що задовольняє даному рівнянню, почаковій умові та крайовим умовам .

Використовуючи метод сіток, вибирають крок по осі 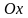та обчислюють крок 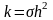по осі 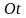, а потім будують сітку зі значеннями .

Значення 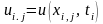обчислюють за формулами:

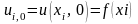- з початкової умови,

- з крайових умов.

Для визначення значень у внутрішніх точках застосовують формули:

при ,

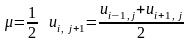при .

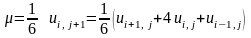3⁰. Змішана задача для рівняння коливання струни полягає в знаходженні функції , що задовольняє даному рівнянню, початковим умовам 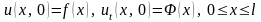та крайовим умовам , .

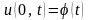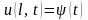Викотовуючи метод сіток, вибирають крок по осях і та будують сітку зі значеннями .

Для визначення значень функції 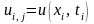застосовують формули:

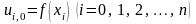- нульовий шар;

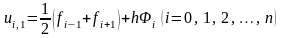- перший шар;

.

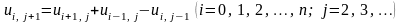РОБОТА 1

Завдання.

Використовуючи метод сіток, знайти наближений розв'язок задачі Дирихлє для рівняння Лапласа в квадраті з вершинами , , , 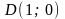; крок 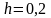. При розв'язуванні задачі використати ітераційний процес усереднення Лібмана до одержання відповіді з точністю .

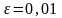В таблиці варіантів наведено формули, що задають шукану функцію на сторонах квадрата .

Номер варіанта
1			0	0
2
3		0	0
4		20
5	0
6
7
8
9		40	40
10			0
11		20
12				0
13
14			0
15				0
16			30	30
17
18	0			0
19		20
20			0
21
22
23
24	40	40
25			0
26		25
27				0
28
29			0
30				0

Зразок виконання завдання , , , .

Процес розв'язування розіб'ємо на декілька етапів.

1. Побудуємо область розв'язку, покривши її сіткою з кроком (рис.1); обчислимо значення шуканої функції 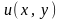в граничних точках області.

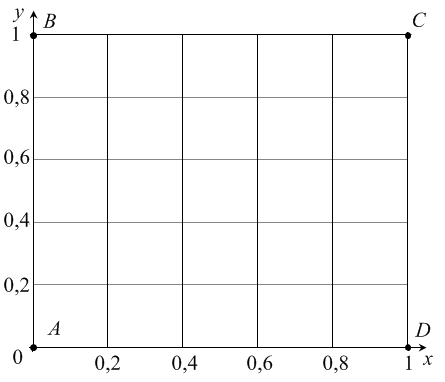
Рис. 1

Рис. 2

1. Значення функції на стороні знайдемо за формулою 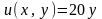; маємо ; ; ; ; ; .

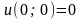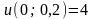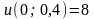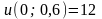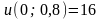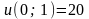2. На стороні : ; ; ; ; ; ; .

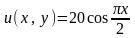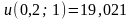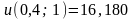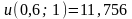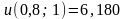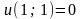3. На стороні : ; ; ; ; ; ; .

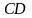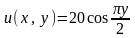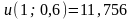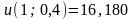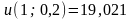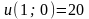4. На стороні : ; ; ; ; ; ; .

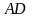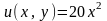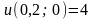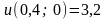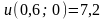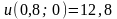2. Скориставшись схемою розміщення вузлів зображених на рис.3, для визначення значень функції у внутрішніх точках області методом сіток задане рівняння Лапласа в кожній точці замінимо скінченно-різницевим рівнянням за формулою:

.

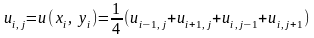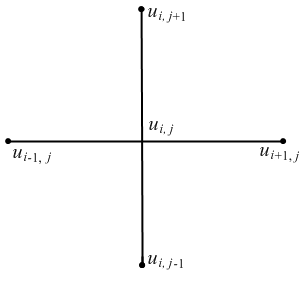
Рис. 3

Використовуючи останню формулу, складемо рівняння для кожної внутрішньої точки. Попередньо пронумеруємо шукані значення функції, зобразивши їх на рис.2, що відповідають побудованій вище сітковій області; на цьому рисунку відмітимо також знайдені граничні значення.

У результаті одержимо систему рівнянь

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; .

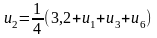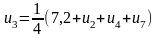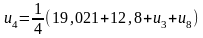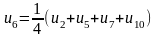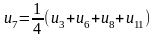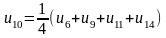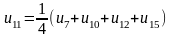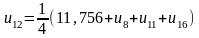Розв'язування цієї системи проведемо ітераційним способом Зейделя. Для кожного значення складемо послідовність 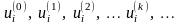, яку будуємо до збіжності в сотих частинах. Запишемо співвідношення, за допомогою яких будемо знаходити елементи всіх послідовностей:

; ;

; ;

; ;

; ;

; ;

; ;

; ;

; .

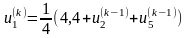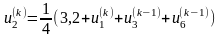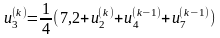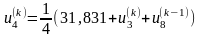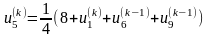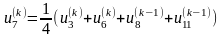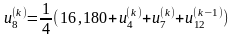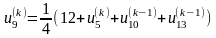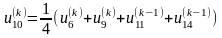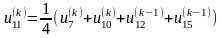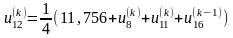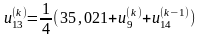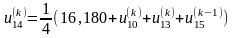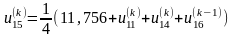Для обчислень за цими формулами потрібно визначити початкові значення , які можна знайти одним з відомих способів.
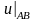
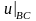
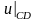
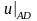
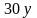
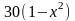
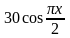
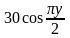
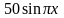
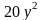
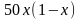
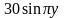
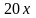
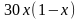
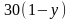
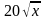
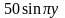
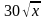
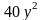
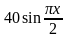
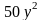
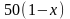
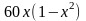
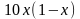
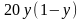
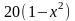
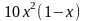
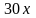
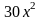
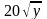
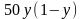
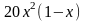
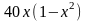
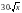
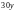
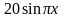
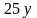
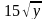
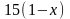
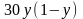
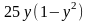
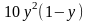
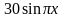
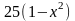
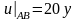
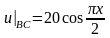
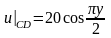