1.5. Повторные независимые испытания

Формула Бернулли

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события А постоянна и равна и не равна 0 и 1, событие А наступит ровно раз, вычисляется по формуле Бернулли:

, где . (1.15)

Локальная теорема Лапласа

При большом числе испытаний для решения подобных задач

применяется формула

, (1.16)

где и .

Функция φ (х) – чётная, т.е. φ(-х) = φ (х). Функция φ (х) табулированная на отрезке [0; 4], поэтому для х ≥ 4 функция φ (х) ≈ 0.

В приложении А приведена таблица значений этой функции.

Теорема Пуассона

Если вероятность наступления события А в каждом испытании стремится к 0 ( →0) при неограниченном увеличении числа испытаний ( →∞), причем произведение стремится к постоянному числу , то вероятность того, что событие А из испытаний наступит раз находится по формуле . (1.17)

В приложении В приведена таблица значений этой функции.

Интегральная теорема Лапласа

вероятность того, что событие наступает не менее раз и не более раз приближенно равна

(1.18)

где  функция Лапласа.

Ф(х) нечётная, т.е. Ф(-х) = Ф(х), для х > 5 Ф(х) ≈ 0,5.

В приложении Б приведена таблица значений функции Лапласа.

Формулы Бернулли, Лапласа и Пуассона применяются в тех случаях, когда рассматриваются испытания , удовлетворяющие схеме Бернулли, т.е.

• проводимые испытания независимы;

• каждое испытание имеет только два исхода;

• вероятность появления события в каждом испытании постоянна и равна .

При этом важно правильно выбрать соответствующую формулу: (1.15), (1.16), (1.17), (1.18).

Указания. При выборе формулы можно руководствоваться следующим:

1. Если число независимых испытаний 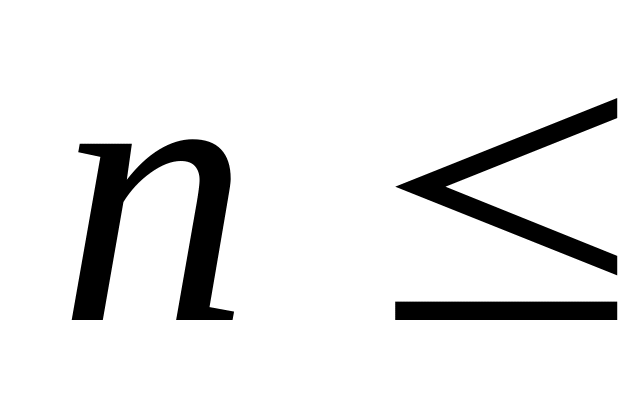10, то для вычисления вероятности появления события m раз пользуются формулой Бернулли (1.15).

2. Если число независимых испытаний 10 и требуется найти вероятность появления события от до раз, то используется формула .

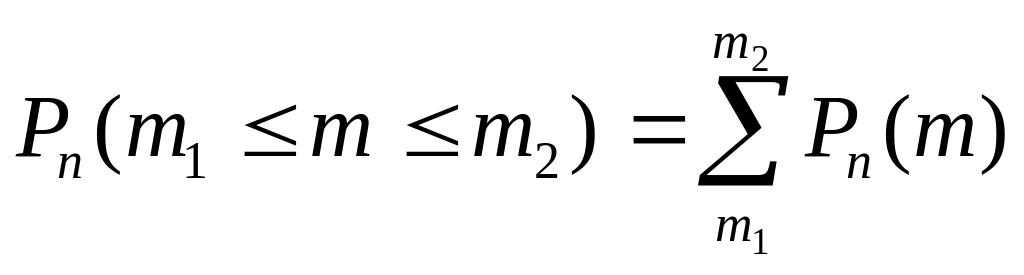3. Если число независимых испытаний n достаточно велико, а вероятность появления события в каждом испытании мала (стремится к 0) и , то для вычисления вероятности применяют формулу Пуассона (1.17).

4. Если число независимых испытаний n достаточно велико, вероятность появления события в каждом испытании отлична от 0 и 1, то для вычисления применяют формулу (1.16).

5. Если число независимых испытаний n достаточно велико, то для вычисления вероятности появления события от m₁ до m₂ раз:

а) при малом числе слагаемых в сумме можно применять локальную формулу Лапласа, т.е.

; ( 1.19)

б) при малом числе слагаемых в сумме и малой вероятности появления события в каждом испытании, при применяют формулу Пуассона, т.е.

; (1.20)

в) при достаточно большом числе слагаемых применяется

интегральная теорема Лапласа.

Наивероятнейшее число появления события

Если n – число независимых испытаний, р – вероятность наступления события А в отдельном испытании, то наивероятнейшее число m₀ появления события А удовлетворяет неравенству np – q ≤ m₀ ≤ np + p.

Следствие интегральной теоремы Лапласа

Если вероятность наступления события А в каждом из независимых испытаний постоянна и отлична от 0 и 1, то при достаточно большом числе испытаний вероятность того , что

а) число m наступлений события А отличается от произведения np не более чем на величину ɛ > 0 (по абсолютной величине), т. е.

б) частость события А отличается от его вероятности р не более чем на величину Δ > 0 ( по абсолютной величине ), т.е. _.

Пример 1.16. Вероятность выигрыша по одному любому лотерейному билету равна 0,02. Чему равна вероятность выигрыша для владельца четырёх билетов а) по трём билетам; б) не более чем по двум билетам. Решение: n = 4; p = 0,02 ; q = 0,98.

а) ;

Пример 1.17. Магазин получил 1000 бутылок минеральной воды. Вероятность того, что при перевозке бутылка окажется разбитой, равна 0,003. Найти вероятность того, что магазин получит разбитых бутылок: а) ровно две; б) меньше двух; в) больше одной; г) хотя бы одну.

Решение: Число независимых испытаний =1000 достаточно велико, а вероятность появления события в каждом испытании мала (стремится к 0 ) и , искомую вероятность будем находить по формуле Пуассона (1.17), используя таблицу значений функции (приложение В).

а)

б)

в)

г) .

Пример 1.18. Доля изделий высшего сорта на данном предприятии составляет 90%. Найти вероятность того, что из взятых на проверку 600 изделий: а) высшего сорта окажется 530 изделия; б) из 600 изделий от 520 до 535 изделий (включительно) будут высшего сорта; в) наивероятнейшее число изделий высшего сорта.

Решение. Эксперимент заключается в проведении 600 повторных независимых испытаний с двумя исходами в каждом. Вероятность появления изделия высшего сорта в каждом испытании постоянна. Следовательно, схема Бернулли применима.

а) По условию задачи , , . Так как достаточно велико, а и не малы, то для вычисления искомой вероятности применим локальную теорему Лапласа (1.16) и таблицу значений функции (приложение А) .

, ; ;

;

б) , , . Так как число независимых испытаний достаточно велико и число слагаемых в сумме равно шестнадцати, то для вычисления искомой вероятности воспользуемся интегральной теоремой Лапласа .

Значения функции Лапласа, учитывая её нечётность, находим по таблице (приложение Б)

в) , q=0,1.

Наивероятнейшее число изделий высшего сорта определим по формуле

np – q ≤ m₀ ≤ np + p;

600·0,9 – 0,1 ≤ m₀ ≤ 600·0,9 + 0,9; 539,9 ≤ m₀ ≤ 540,9; m₀=540.

Задачи

117. Вероятность того, что торговая база не превысит дневную норму расходов, равна 0,9. Определите вероятность того, что за пять дней норма дневных расходов будет превышена дважды.

118. Вероятность того, что посетитель магазина совершит покупку, равна 0,6. Найдите вероятность того, что из 8 посетителей покупку сделают:

а) не более двух человек; б) не менее двух человек.

119. Система состоит из шести независимо работающих элементов. Вероятность отказа элементов равна 0,3. Найдите: а) наивероятнейшее число отказавших элементов; б) вероятность наивероятнейшего числа отказавших элементов системы; в) вероятность отказа системы, если для этого достаточно, чтобы отказали, хотя бы пять элементов.

120. Тест по экономике состоит из 10 вопросов. На каждый вопрос в тесте предлагается 4 варианта ответа, из которых нужно выбрать один правильный. Какова вероятность того, что, будучи совершенно не готовым к тесту, студент угадает правильные ответы, по крайней мере, на 6 вопросов?

121. Два равносильных противника играют в шахматы. Что вероятнее: а) выиграть одну партию из двух или две партии из четырёх; б) выиграть не менее двух партий из четырёх или не менее трёх партий из пяти (ничьи во внимание не принимаются)?

122. Вероятность хотя бы одного попадания при двух выстрелах равна 0,96. Найдите вероятность трёх попаданий при четырёх выстрелах.

123. Сколько раз следует двукратно подбросить монету, чтобы с вероятностью не менее 0,95 хотя бы один раз появилось событие «один герб и одна решка»?

124. Игральная кость брошена 9 раз. Найдите наивероятнейшее число очков, кратное трём, и вычислите его вероятность.

125. Сколько раз нужно бросить игральную кость, чтобы наивероятнейшее число появлений чётного числа очков было равно 6?

126. Аудиторную работу по теории вероятностей с первого раза успешно выполняют 60% студентов. Найдите вероятность того, что из 400 студентов работу успешно выполнят 265 студентов.

127. По результатам проверок налоговыми инспекциями установлено, что в среднем каждое третье малое предприятие региона имеет нарушение финансовой дисциплины. Найдите вероятность того, что из 1200 зарегистрированных в регионе малых предприятий имеют нарушения финансовой дисциплины: а) 410 предприятий; б) наивероятнейшее число таких предприятий.

128. Производители калькуляторов знают из опыта, что 2% проданных калькуляторов имеют дефекты. Аудиторская фирма купила 500 калькуляторов. Какова вероятность того, что придётся заменить: а) 4 калькулятора; б) не менее трёх калькуляторов?

129. Вероятность производства стандартной детали в некоторых условиях равна 0,97. Найдите наивероятнейшее число стандартных среди 625 деталей и вероятность такого числа деталей.

130. Сборник задач содержит 400 задач с ответами. В каждом ответе может быть ошибка с вероятностью 0,01. Какова вероятность, что 98% всех ответов на задачи сборника приведены без ошибок?

131. Вероятность того, что пассажир опоздает к отправлению поезда, равна 0,012. Найдите наиболее вероятное число опоздавших из 900 пассажиров и вероятность такого числа опоздавших.

132. Учебник издан тиражом 2 000 экземпляров. Вероятность того, что экземпляр учебника сброшюрован неправильно, равна 0,003. Найдите вероятность того, что: а) тираж содержит 5 бракованных книг; б) не более 3.

133. Вероятность того, что случайно выбранный лицевой счёт клиента отделения сбербанка содержит ошибки, равна 0,002. Если при выборочной проверке счетов обнаружится, что не менее 0,4% отобранных счетов содержат ошибки, то оператор увольняется с работы. Найдите вероятность того, что оператор будет уволен, если ревизор проверит 400 счетов.

135. Имеется общество из 730 человек. Найти: а) вероятность того, что у трёх человек день рождения приходится на Новый год; б) наиболее вероятное число человек, имеющих один и тот же день рождения и вероятность такого события. Считать, что вероятность рождения в фиксированный день равна

136. В новом микрорайоне поставлено 10 000 кодовых замков на входных дверях домов. Вероятность выхода из строя одного замка в течение месяца равна 0,000 4. Найдите вероятность того, что за месяц: а) откажут пять замков; б) откажут по крайней мере 3 замка; в) будут исправно работать 9 997 замков; г) будут исправно работать хотя бы 9 997 замков.

137. Завод отправил на базу 15 000 стандартных изделий. Среднее число изделий, повреждаемых при транспортировке, составляет 0,06%. Найдите вероятность того, что из 15 000 изделий будет повреждено от двух до пяти изделий.

138. Магазин произвёл 50 распродаж по сниженным ценам. Вероятность того, что каждая из них оправдала себя по окупаемости, составляет 0,08. Найдите вероятность, что хотя бы одна из распродаж оказалась неубыточной.

139. Каждый из 100 компьютеров в интернет-кафе занят клиентом в среднем в течение 80% рабочего времени. Какова вероятность того, что в момент проверки клиентом будет занято: а) от 75 до 90 компьютеров; б) не менее 80 компьютеров; в) не более 74 ?

140. На научную конференцию приглашены 130 человек, причём каждый из них прибывает с вероятностью 0,7. В гостинице для участников конференции заказано 95 мест. Какова вероятность, что все приезжающие будут поселены в гостинице?

141. Страховая фирма заключила 10 000 договоров. Вероятность страхового случая по каждому в течение года составляет 2%. Найдите вероятность того, что таких случаев будет не более 250.

142. При обследовании уставных фондов банков установлено, что пятая часть банков имеет уставный фонд свыше 100 млн руб. Найдите вероятность того, что среди 1 800 банков имеют уставный фонд свыше 100 млн руб. от 330 до 400 включительно.

143. Инвестор решил вложить поровну средства в три предприятия при условии возврата ему через определённый срок 150% от вложенной суммы каждым предприятием. Найдите вероятность того, что по истечении срока кредитования инвестор получит обратно, по крайней мере, вложенную сумму, если вероятность банкротства каждого из предприятий равна 0,2.

144. Страховая компания застраховала 1 000 клиентов одного возраста и одной социальной группы. Вероятность смерти клиента в течение года – 0,006. Каждый клиент вносит 1 января 15 долларов. В случае смерти застрахованного лица наследникам выплачивается 1 200 долларов. Чему равна вероятность того, что: а) страховая компания разорится; б) получит более 10 000 долларов прибыли?

145. У страховой компании имеются 10 000 клиентов. Каждый из них, страхуясь от несчастного случая, вносит 500 руб. Вероятность несчастного случая 0,0055, страховая сумма, выплачиваемая пострадавшему, составляет 50 000 руб. Какова вероятность того, что: а) страховая компания потерпит убыток; б) на выплату страховых сумм уйдёт более половины всех средств, поступивших от клиентов; в) на какую прибыль может рассчитывать страховая компания с надёжностью 0,95.

146. В тесто, приготовленное для выпечки 1 000 булочек, засыпают 10 000 изюминок и тщательно перемешивают. Какова вероятность того, что в случайно выбранной булочке будет: а) 5 изюминок; б) меньше 10 изюминок.

147. Мастер и ученик участвуют в шахматном матче. Мастер выигрывает матч, если он выиграл все партии в матче. Ученик выигрывает матч, если он выиграл хотя бы одну партию в матче. Из скольких партий должен состоять матч, чтобы шансы на победу у мастера и ученика были равны, если вероятность победы мастера в одной партии 0,9, а ученика – 0,1?

148. Статистическая вероятность рождения мальчика равна 0,515. Определите вероятность того, что среди 400 новорожденных доля мальчиков будет отличаться от вероятности рождения мальчика по абсолютной величине не более чем: а) на 0,005; б) 0,01; в) 0,04. Как влияет величина допустимого отклонения на значение искомой вероятности?

149. При установившемся технологическом процессе вероятность изготовления бракованного шарика для шарикоподшипника равна 0,15. Определите вероятность того, что доля бракованных шариков среди изготовленных 1 000 шт. будет отличаться от вероятности изготовления бракованного шарика не более чем на 0,003 в ту или иную сторону. Как изменится результат, если шариков 625 шт.? Как влияет число отбираемых шариков на величину искомой вероятности?

150. Французский учёный Бюффон в 1777г. бросил монету 4 040 раз,

причём «герб» появился 2 048 раз. Найти вероятность того, что при повторении опыта Бюффона относительная частота появления «герба» отклонится от вероятности появления «герба» по абсолютной величине не более чем в опыте Бюффона.

151. Вероятность попадания в цель при каждом выстреле постоянна и равна 0,8. Найдите число выстрелов, необходимых для того, чтобы с вероятностью 0,954 4 относительная частота попаданий в цель отличалась от вероятности 0,8 по абсолютной величине не более чем на 0,01.

152. 90% семян всходят. Найдите наименьшее отклонение (по абсолютной величине) частости взошедших семян из 2 000 посеянных от вероятности 0,9, которое можно ожидать с вероятностью 0,990 7.

153. Найдите границы, в которых с вероятностью 0,861 2 находится относительная частота родившихся девочек из 2 500 новорождённых. Вероятность рождения девочки принять равной 0,485.

154. Для определения нормы высева требуется определить всхожесть семян с точностью до 0,01 и надёжностью 0,956 6. 80% семян всходят после посева, сколько семян следует проверить?

155. Среди проверенных наудачу отобранных 2 500 изделий из массовой продукции цеха оказалось 300 шт. бракованных. Определить вероятность того, что отклонение эмпирически установленной доли брака от доли брака во всей продукции цеха не превысит по абсолютной величине 0,01. Указание: доля брака во всей продукции цеха принимается равной вероятности того, что наудачу взятое изделие из всей продукции окажется бракованным.

156. Вероятность изготовления нестандартной микросхемы равна 0,02. Какое количество микросхем следует отобрать, чтобы с вероятностью 0,910 8 можно было утверждать, что доля среди них нестандартных микросхем будет отличаться от вероятности изготовления нестандартной микросхемы по абсолютной величине не более чем на 0,05?

157. Вероятность того, что из наудачу взятого яйца выведется петушок, равна 0,52. В инкубатор заложили 38 500 яиц. Определите вероятность того, что среди выведенных цыплят число курочек будет отличаться от наиболее вероятного числа по абсолютной величине не более чем на 208 штук.

158. Известно, что 83% изделий, выпускаемых цехом по единой технологии, высшего качества. Определите вероятность того, что число изделий высшего качества среди 1 200 изготовленных будет по абсолютной величине отличаться от наиболее вероятного их числа не более чем на 10.

159. Отдел технического контроля проверяет на стандартность 900 изделий. Вероятность того, что деталь стандартна, равна 0,9. Найти с вероятностью 0,954 4 границы, в которых будет заключено число m стандартных деталей среди проверенных.

160. На керамическом заводе 70% тарелок выпускается продукцией первого сорта. ОТК завода должен проверить партию из 600 изготовленных тарелок. Какое предельное отклонение (по абсолютной величине) числа первосортных тарелок от наиболее вероятного их числа можно гарантировать с вероятностью 0,99?

161. В среднем 85% заёмщиков возвращают кредит в срок. Банк предоставил кредит 600 клиентам. Найдите вероятность того, что отклонение числа клиентов, не оплативших кредит в срок, от наивероятнейшего числа не превзойдёт 6.

162. Вероятность того, что студент воспользуется услугами банкомата 0,25. Оценить, что услугами банкомата воспользуются от 45 до 55 студентов из двухсот. Найдите вероятность того, что отклонение числа студентов, которые воспользуются банкоматом, от наивероятнейшего числа не превзойдёт трёх.

163. Игральную кость бросают 80 раз. Найдите приближённо границы, в которых число выпадений шестёрки будет заключено с вероятностью 0,997.

164. Вероятность поломки радиолампы в течение года – 0,1. В крае находится в эксплуатации 10 000 таких ламп. Каков должен быть объём запаса таких ламп, чтобы с надёжностью 0,95 обеспечить потребность в замене ламп?