1.4. Формула полной вероятности. Формула Байеса
Формула полной вероятности
Если событие А может произойти с одной из попарно несовместных гипотез Н1, Н2,….Нn, образующих полную группу, то вероятность появления события А равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события А:
,
(1.13)
где
.
Формула Байеса
Формула Байеса определяет условную вероятность появления гипотезы
Hi, при условии, что событие А уже произошло:
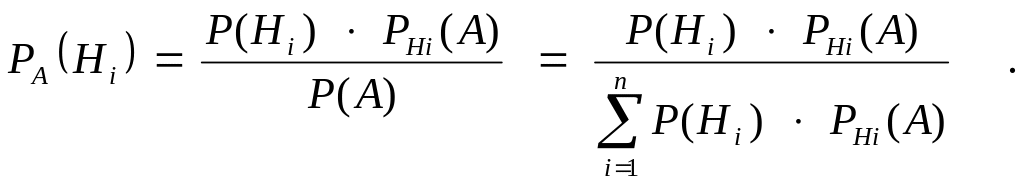(1.14)
Пример 1. 14. Фирма имеет три источника поставки комплектующих – фирмы А, В, С. На долю фирмы А приходится 50% общего объёма поставок, В – 30% и С-20%. Из практики известно, что 10% деталей, поставляемых фирмой А – бракованные, фирмой В – 5% и С − 6%. Найти вероятность того, что наудачу выбранная деталь будет бракованной.
Решение: Производится испытание: извлекается одна деталь.
Событие А – извлечённая деталь бракованная .
Гипотеза Н1 – деталь фирмы А; гипотеза Н2 – деталь фирмы В; гипотеза Н3 – деталь фирмы С.
Согласно формуле полной вероятности (1.13), искомая вероятность равна:
.
Из
условия задачи:
;
;
.
;
;
.
Р(А) = 0,5 0,1 + 0,3 0,05 + 0,2 0,06 = 0,077.
Пример 1.15. В центральную бухгалтерию корпорации поступили пачки накладных для проверки и обработки. 90% пачек были признаны удовлетворительными: они содержали только 1% неправильно заполненных накладных. Остальные 10% пачек были признаны неудовлетворительными, так как содержали 5% неверно оформленных накладных. Взятая наугад из пачки накладная оказалась оформленной неверно, какова вероятность того, что пачка накладных, из которой изъята накладная признана неудовлетворительной ?
Решение: Испытание: проверяется пачка накладных. Событие А − взятая наугад накладная оказалась неверно оформленной.
Гипотеза Н1 − пачка не соответствует стандарту.
Гипотеза Н2 − пачка соответствует стандарту.
Необходимо найти вероятность гипотезы Н1 при условии, что событие А произошло. Согласно формуле Байеса (1.14) имеем:
;
;
;
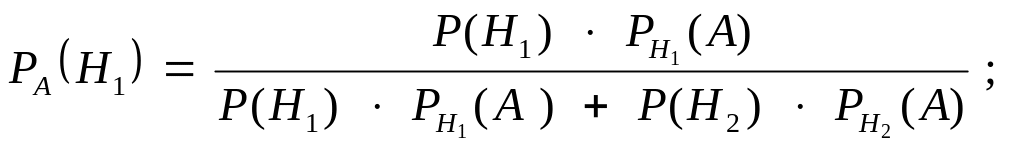
Задачи
96. На складе хранится 10 изделий компании А, 15 изделий компании В и 30 изделий компании С. Вероятность того, что А производит изделия высшего сорта, равна 0,9, В – 0,8 и С − 0,7. Найдите вероятность того, что случайно выбранное изделие окажется высшего сорта.
97. Вероятности обращения фирмы за кредитом в один из четырёх банков соответственно равны р1 = 0,3, р2 = 0,2, р3 = 0,4 и р4 = 0,1. Вероятность отказа в кредите в первом банке равна 0,4, во втором − 0,5, в третьем и четвёртом банках эти вероятности соответственно равны 0,2 и 0,7. Найдите вероятность того, что фирма получит кредит после обращения в наугад взятый банк.
98. Из имеющегося набора карточек с буквами, составляющими слово "экономика", наугад взяли две карточки, после чего случайным образом взяли ещё одну. Какова вероятность того, что карточка будет с гласной буквой?
99. В торговую фирму поступили телевизоры от трёх поставщиков в отношении 1:4:5. Практика показала, что телевизоры, поступающие от 1-го, 2-го, и 3-го поставщиков, не потребуют ремонта в течение гарантийного срока соответственно в 98%, 88% и 92% случаев. Найдите вероятность того, что поступивший в продажу телевизор не потребует ремонта в течение гарантийного срока.
100. Для изготовления продукции используются детали четырёх заводов. Первый завод поставил 2 000 деталей, второй − 1 700, третий − 200 и четвёртый поставил 2 000. Известно, что процент бракованных деталей среди продукции первого завода составляет 0,2%, второго − 0,3%, третьего − 0,2% и четвёртого − 0,5%. Какова вероятность того, что наугад взятая деталь окажется бракованной?
101. В вычислительной лаборатории имеется 6 персональных компьютеров одного типа и 4 другого. Вероятность того, что за время работы компьютер первого типа не выйдет из строя, равна 0,999, а для компьютеров второго типа эта вероятность равна 0,99. Студент сел выполнять работу за наугад выбранный компьютер. Найдите вероятность того, что до окончания работы компьютер не выйдет из строя.
102. Электрические лампочки изготавливаются на трёх заводах. Первый из этих заводов поставляет 40% общего количества, второй − 35% и третий − 25%. Продукция первого завода содержит 80% стандартных ламп, второго − 90%, третьего − 98%. Все изготовленные лампочки поступают в магазин. а) Какова вероятность того, что купленная в магазине лампочка окажется стандартной? б) Купленная лампочка оказалась стандартной. Найти вероятность того, что она изготовлена на первом заводе.
103. Страховая компания разделяет застрахованных по классам риска: I класс – малый риск, II – класс средний, III класс – большой риск. Среди клиентов компании 50% − первого класса риска, 30% − второго и 20% − третьего. Вероятность выплаты страхового вознаграждения для клиента первого класса риска 0,01, для второго – 0,03, для третьего – 0,08. а) Какова вероятность того, что застрахованный клиент получит денежное вознаграждение за период страхования. б) купленная лампочка. б) Застрахованный клиент получил страховое вознаграждение. Найти вероятность того, что он относится к III классу риска.
104. В специализированную больницу поступают в среднем 55% больных с заболеванием А, 25% − с заболеванием В, 20% − с заболеванием С. Вероятность полного излечения болезни А равна 0,7, для болезней В и С эти вероятности соответственно равны 0,8 и 0,9. Больной, поступивший в больницу, был выписан здоровым. Найдите вероятность того, что этот больной страдал заболеванием С.
105. Два бухгалтера обрабатывают равное количество счетов. Вероятность того, что первый бухгалтер допустит ошибку, равна 0,005, для второго эта вероятность равна 0,01. При проверке счетов была найдена ошибка. Найдите вероятность того, что её допустил первый бухгалтер.
106. Имеется три группы студентов. В первой группе 24 человека, во второй − 26 и в третьей − 20. Экзамен по теории вероятностей сдали на «отлично» в первой группе 6 человек, во второй − 7 и в третьей группе − 4 студента. На общем собрании студентов этих групп выбирают случайным образом одного студента. Какова вероятность того, что выберут студента первой группы, сдавшего экзамен по теории вероятностей на «отлично»?
107. Коллектив академии избирает ректора. Среди избирателей 30% − преподаватели, 60% − студенты и 10% − прочий персонал. Вероятность того, что преподаватель проголосует за определённого кандидата, равна 0,7, среди остальных избирателей эта вероятность равна 0,5. Найдите вероятность того, что кандидат будет избран (кандидат считается избранным, если за него проголосовало более 50% избирателей).
108. Число грузовых автомашин, проезжающих по шоссе, на котором стоит автозаправочная станция, относится к числу легковых машин как 2:3. Вероятность того, что проезжающая грузовая машина будет заправляться, равна 0,1, для легковой машины эта вероятность равна 0,2. К автозаправочной станции подъехала для заправки машина. Найдите вероятность того, что это грузовая машина.
109. Два охотника стреляют одинаковыми пулями в медведя. В результате медведь был убит одной пулей (событие А). Как охотники должны поделить шкуру убитого медведя, если известно, что вероятность попадания у первого охотника 0,3, а у второго – 0,6?
110. Уголь закупается у двух поставщиков А и В. Если в течение четырёх дней уголь не поступает, то производственный процесс останавливается. Вероятность того, что уголь поступит в 4 дня от А равна 0,6, от В – 0,35. Производственный процесс не был остановлен в 4 дня. Найти вероятность того, что уголь поступил от поставщика В.
111. Некто, заблудившись в лесу, вышел на поляну, откуда вели 4 дороги. Известно, что вероятности выхода из леса за час для различных дорог равны соответственно 0,6; 0,3; 0,2; 0,1. Чему равна вероятность того, что заблудившийся пошёл по первой дороге, если известно, что через час он вышел из леса?
112. На Дальнем Востоке 70% совместных предприятий занимаются экспортно-импортной деятельностью, остальные 30% – производители. В конце года 10% первых и 4% вторых не предоставили деклараций в налоговую инспекцию. Найти вероятность того, что: а) предприятие является компанией-производителем, если оно нарушило законодательство; б) найти вероятность того, что случайно выбранное предприятие является законопослушным.
113. Экономист полагает, что в течение периода активного экономического роста американский доллар будет расти в цене с вероятностью 0,7, в период умеренного экономического роста он подорожает с вероятностью 0,4 и при низких темпах роста – с вероятностью 0,2. Вероятность активного экономического роста в стране оценивается аналитиками как 0,3; умеренного экономического роста – 0,5 и низкого роста 0,2. Предположим, что доллар дорожает в течение текущего периода. Чему равна вероятность того, что анализируемый период совпал с периодом активного экономического роста?
114. Из числа авиалиний некоторого аэропорта 60% – местные, 30%– по странам СНГ и 10% – в страны дальнего зарубежья. Среди пассажиров местных авиалиний 50% путешествуют по делам, связанным с бизнесом, на линиях СНГ – 60%, на международных – 90%. Из прибывших в аэропорт пассажиров случайно выбирается один. Чему равна вероятность того, что он: а) бизнесмен; б) прибыл из стран СНГ по делам бизнеса; в) прибыл местным рейсом по делам бизнеса; г) прибывший международным рейсом бизнесмен.
115*. Задача о разорении1. Петя с папой играют в следующую игру. Петя бросает монету, предварительно сообщив папе, какая сторона, по его мнению, выпадет: «герб» или «решка». Если Петя угадал, то папа платит Пете 1 руб., в противном случае Петя платит папе рубль. Начальный капитал Пети составляет х = 100 руб. Игра продолжается до тех пор, пока Петя не наберёт заранее определённую сумму s, либо пока он не разорится, проиграв весь имеющийся капитал x. Найти вероятность того, что Петя разорится, так и не набрав желаемую сумму, если эта сумма s составляет:
а) 110 руб.; б) 1 000 руб.
116*. Задача о разборчивой невесте2. У одной из Машиных подруг есть достаточно большое число женихов. Заранее она о своих женихах ничего не знает, кроме их числа n. Расположившись в очередь в случайном порядке, женихи представляются разборчивой невесте один за другим так, что встречая очередного жениха, она знает всех предыдущих. Представленный и отвергнутый жених больше не возвращается. Невеста решила избрать следующую стратегию выбора: она просматривает первых m женихов, никого из них не выбирая, а затем останавливает свой выбор на первом из оставшихся (n – m) женихов, который окажется лучше, чем любой из первых m женихов. Найти вероятность Pm(A) сделать наилучший выбор при такой стратегии. Определить такое число m*, чтобы вероятность Pm* (A) была максимальной среди всех Pm(A), m=0,1… ,n.