Операции над матрицами

Над матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциям над числами, а некоторые – специфические.

1. Умножение матрицы на число. Произведением матрицы А на число λ называется матрица B=λA, элементы которой b_ij = λa_ij для i =1,2, … , m; j = 1, 2, …, n.

Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы. В частности, произведение матрицы А на число 0 есть нулевая матрица, т.е. 0*А= 0.

2. Сложение матриц. Суммой двух матриц A и B одинакового размера m*n называется матрица C = A+B, элементы которой c_ij = a_ij + b_ij для i=1, 2, …, m; j= 1, 2, …, n ( т.е. матрицы складываются поэлементно)

3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A- B = A + (-1)*B.

4. Умножение матриц. Умножение матрицы A на матрицу B определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц называется такая матрица 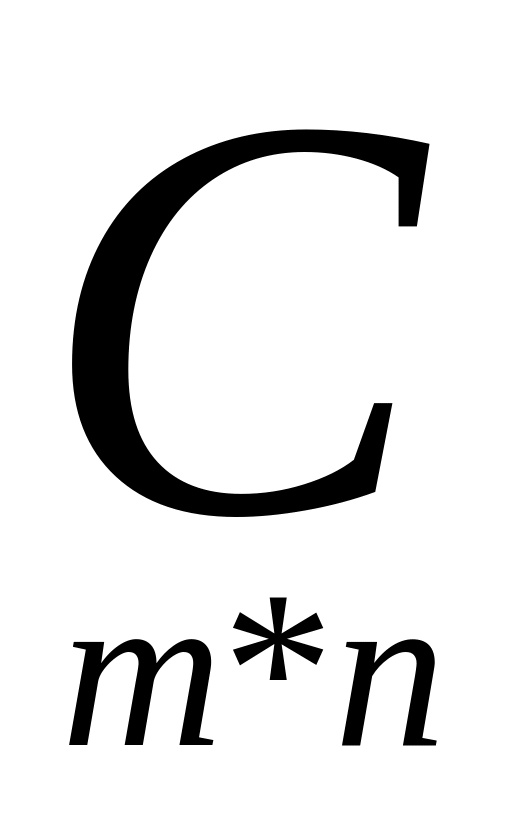, каждый элемент которой c_ij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы B:

С_ij = a_i1b_1j + a_i2b_2j + … + a_ikb_kj = =1, 2, …, m; j = 1, 2, …, n.

Транспонирование матрицы – переход от матрицы А к матрице А^, , в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А^, называется транспонированной относительно матрицы А.

Н апример, А_2*3 = 1 2 3 А^, = 1 4

4 5 6 2 5

3 6