1. Общие сведения

Планирование ремонтов агрегатов тракторов и комбайнов

при отсутствии исходной информации

Исходные данные для планиро­вания:

1. Средний доремонтный или межремонтный ресурс агрегата – _др или _мр.

2. Плановая наработка (в пересчете на одну машину) – Н_пл.

3. Фактическая наработка от последнего ремонта до начала пла­нового периода (в пересчете на одну машину) – Н_ф.

4. Коэффициент вариации – V.

В случае закона нормального распределения (ЗНР) суммарное ко­личество ремонтов N_р за плановый период определяют по формуле

N_р = N * F_o (Н_ф + Н_пл - _{мр (др)} ) / (V _{мр (др)}) ,

где N – количество планируемых агрегатов данной марки;

F_o – интегральная нормированная функция распределения, опре­деляемая по таблице П.2 приложения.

Верхнюю границу наработки до постановки в ремонт отдельного агрегата определяют по формулам

Если выполняется неравенство № _i / (N + 1) < 0,5, по формуле

= _{мр (др)} [1 – VН_к{1 - № _i / (N + 1)}] - Н_ф (2)

В случае неравенства № _i / (N + 1) > 0,5, по формуле

= _{мр (др)} [1 + VН_к{1 - № _i / (N + 1)}] - Н_ф (3)

где № _i – порядковый номер агрегата, отправляемого в ремонт;

Н_к – квантиль ЗНР, величину которого определяют по таблице П.7 приложения

Ход работы

ЗАДАЧА

В хозяйстве эксплуатируют 10 тракторов ДТ-75. Составить план ремонтов тракторов (двигателей) при Н_ф = 800 мото-ч и Н_пл = 2000 мото-ч.

Собственной исходной информации о ресурсах двигателей в хозяйстве нет. По зоне установлена для них средняя величина межремонтного ресурса _мр = 1800 мото-ч.

Решение

1. Задаваясь величиной коэффициента вариации V = 0,40, определить I суммарное количество ремонтов двигателей за плановый период по уравнению

N_р = 10 F_o(800 + 2000 – 1800) / (0,4*1800) = 10 F_o(1,39)

По таблице П.2 приложения F_o(1,39) = 0,92, тогда

N_р = 10 • 0,92 10 ремонтов двигателей.

2. Определить верхнюю границу наработки до ремонта первого двигателя по уравнению (2) (так как =0,09 < 0,50)

По таблице П.7 приложения Н_к (0,91) = 1,34, тогда

= 1800 [1 – 0,4Н_к{1 - 1 / (10 + 1)}] – 800 40 мото-ч

Нижняя граница наработки до ремонта первого двигателя — начало пла­нового периода ( = 0 мото-ч).

3. Определить верхнюю границу наработки до ремонта второго двигателя по уравнению (2) (так как < 0,50 )

= 1800 [1 – 0,4Н_к{1 - 2 / (10 + 1)}] – 800 340 мото-ч

Нижняя граница наработки до ремонта второго двигателя есть верхняя гра­ница наработки до ремонта первого двигателя

= = 40 мото-ч

и т. д. до ремонта шестого двигателя.

= 580 мото-ч; = 760 мото-ч; = 920 мото-ч.

4. Определить верхнюю границу наработки до ремонта шестого двигателя по уравнению (3) (так как = 0,55 > 0,50 )

= 1800 [1 + 0,4Н_к{6 / (10 + 1)}] – 800 1090 мото-ч

и т. д. до конца планового периода (до ремонта десятого трактора).

= = 1800 [1 + 0,4Н_к{7 / (10 + 1)}] – 800 = 1800 [1 + 0,4Н_к (0,64) ] – 800 = 1800 (1 + 0,4*0,358) – 800 1258 мото-ч;

= = 1800 [1 + 0,4Н_к{8 / (10 + 1)}] – 800 = 1800 [1 + 0,4Н_к (0,73) ] – 800 = 1800 (1 + 0,4*0,613) – 800 1442 мото-ч;

= = 1800 [1 + 0,4Н_к{9 / (10 + 1)}] – 800 = 1800 [1 + 0,4Н_к (0,82) ] – 800 = 1800 (1 + 0,4*0,915) – 800 1659 мото-ч;

= 1800 [1 + 0,4Н_к{10 / (10 + 1)}] – 800 = 1800 [1 + 0,4Н_к (0,91) ] – 800 = 1965 мото-ч.

При больших плановых наработках Н_пл может возникнуть необхо­димость повторных ремонтов машин. Количество повторных ремонтов суммируют с количеством ремонтов, рассчитанных по уравнению (1).

Первый повторный ремонт планируют, если

Н_пл - _мр

Второй повторный ремонт планируют при

Н_пл - _мр

и т. д.

Если _мр > Н_пл, повторные ремонты не планируют. Так, в задаче:

2000 — 40 = 1960 > 1800 — добавить один повторный ремонт,

2000 — 340 = 1660 < 1800 — второго повторного ремонта не планировать.

Таким образом с учетом необходимости проведения одного повторного ремонта, общее количество планируемых ремонтов N_р = 11.

Планирование ремонтов при наличии полной информации о

ресур­сах

План наблюдения NUN. Зна­чения среднего доремонтного (межремонтного) ресурса _{мр (др)} и коэффициента вариации V определя­ют в результате обработки полной информации. Н_пл = 2000 мото-ч, Н_ф = 800 мото-ч.

Таблица 1.1 – Информация по доремонтным ресурсам 10 двигателей тракторов ДТ-75М (план NUN)

Номер наблюдаемого трактора	Доремонтный ресурс, мото-ч	Номер наблюдаемого трактора	Доремонтный ресурс, мото-ч
1 2 3 4 5	1500 1520 1610 2010 2870	6 7 8 9 10	2980 3120 3160 3230 3330

Так как объем выборки N = 10 < 25, статистический ряд не строится.

У многих ПН машин начало рассеивания смещено относительно их нулевого значения (ресурс, стоимость, время восстановления работоспособности и др.). Смещение начала рассеивания t _см определяют по формуле

t _см = t ₁ – 0,5(t ₃- t ₁),

где t ₁ и t ₃ – значения первой и третьей точек информации в порядке их возрастания.

Среднее значение ПН рассчитывают по формуле

= t_i / N,

где t_i- значение i – го показателя надежность, мото-ч;

N – объем выборки.

Среднее квадратическое отклонение рассчитывают по формуле

= ( t_i - )² / (N – 1)

Коэффициент вариации V является относительной характеристикой рассеивания ПН и используется при предварительном выборе и оценке ТЗР.

V = / ( -t _см)

Если коэффициент вариации V меньше 0,5, для планирования ре­монтов рекомендуется применять ЗНР, а суммарное количество ремонтов N_р и наработки до ремонта отдельных тракторов определять по уравнениям (1), (2) и (3).

Если V > 0,5, используют закон распределения Вейбулла (ЗРВ) и расчет ведут в cледующей последовательности.

1. Пользуясь таблицей П.11 приложения, определяют по величине коэффициента вариации параметр Вейбулла b и коэффициент K_b

2. По уравнению a = ( _{мр (др)} – t_см) / K_b определяют параметр Вейбулла – а,

смещение t_см определяют по уравнениям

t _см = t ₁ – (t ₃ - t ₁) / 2 или t _см = t _1н – 0,5А,

где – t ₃ и t ₁ первый и третий ПН в порядке возрастания;

t _1н – начало первого интервала статистического ряда.

3. Суммарное количество ремонтов N_р определяют по уравнению

N_р = F (от 0 до Н_ф + Н_пл), (4)

где F — интегральная функция ЗРВ, определяемая по таблице П.3 приложения. Для входа в таблицу П.3 необходимо вычислить отношение

(Н_ф + Н_пл - t_см) / а

Верхнюю границу наработки до постановки в ремонт i-ой машины определяют по уравнению

= а* {( № _i / (N + 1)} + t_см - Н_ф, (5)

где — нормированный квантиль ЗРВ, определяемый по таблице П.8 приложения.

За нижнюю границу наработки до ремонта i-го трактора

принимают верхнюю границу наработки до ремонта предыдущего трактора = .

Решение

Смещение начала рассеивания t _см

t _см = 1500 – (1610-1500) / 2 = 1390 мото-ч

Среднее значение ПН

= 2533 мото-ч

Среднее квадратическое отклонение

= 4269792 / (10 – 1) = 688,8 689 мото-ч

Коэффициент вариации V

V = 689 /(2533 – 1390) = 689 / 1143 = 0,602

Так как V = 0,602 > 0,5, выбираем ЗРВ. Далее выполняется расчет по формулам (4), (5).

При больших плановых наработках Н_пл может возникнуть необхо­димость повторных ремонтов машин. Количество повторных ремонтов суммируют с количеством ремонтов, рассчитанных по уравнению (4).

Первый повторный ремонт планируют, если

Н_пл - _мр

Второй повторный ремонт планируют при

Н_пл - _мр

и т. д.

Практическая работа № 4, 5

Обработка полной статистической информации о ресурсе машин

Методика статистической обработки полной информации

Обработка полной информации содержит следующие этапы [4]:

1. Построение статистического ряда исходной информации и опре-

деление смещения начала рассеивания.

2. Определение среднего значения ПН и среднего квадратичeского отклонения .

3. Проверка информации на выпадающие точки.

4. Построение гистограммы, полигона и кривой накопленных опытных вероятностей.

5. Определение коэффициента вариации V.

6. Проверка совпадения опытных и теоретических законов распределения ПН по критериям соответствия.

Графическое построение интегральной F(t) и дифференциальной f(t) функций ТЗР.

7. Определение доверительных границ рассеивания одиночных и средних ПН и наибольшей возможной ошибки переноса.

Статистический ряд составляют при объеме выборки N ≥ 25 для

упрощения дальнейших расчетов (без потерь точности).

Количество интервалов статистического ряда n определяют по условию n = 8…12.

Длину интервала статистического ряда А рассчитывают по формуле

А = (t _max – t _min) / n,

где t _max и t _min – максимальная и минимальная точки информации соответственно (в курсовой работе это информация об износах) мм.

У многих ПН машин начало рассеивания смещено относительно их нулевого значения (ресурс, стоимость, время восстановления работоспособности и др.). Смещение начала рассеивания t _см определяют по формуле

t _см = t _1н – 0,5А,

где t _1н – начало первого интервала, мм.

Значение опытной вероятности в i –м интервале Р_i определяют по формуле

Р_i = m_i / N,

где m_i – опытная частота i – го интервала.

Полученные данные вносят в табл.1.

Таблица 1. Информация об интервалах исходного статистического ряда

Номер i – го интервала	Границы i – го интервала tiн - tiк, мм	Середина i – го интервала , мм	Частота i – го интервала	Опытная вероятность i – го интервала Рi
1 2 … n

Среднее значение ПН рассчитывают по формуле

= , (1)

где t_ic- значение середины i – го интервала, мм;

Р_i – опытная вероятность i – го интервала.

Среднее квадратическое отклонение рассчитывают по формуле

= (2)

В опытной информации о ПН могут быть ошибочные точки, выпадающие из общего закона распределения. Поэтому перед окончательной математической обработкой информацию проверяют на выпадающие точки по критерию Ирвина.

,

где – опытное значение критерия Ирвина;

t_i, t_i-1 – смежные точки информации.

Теоретический коэффициент Ирвина определяют по значениям объема выборки N и доверительной вероятности , используя таблицу П.1 приложения.

Точка информации является достоверной, если выполняется условие , в противном случае точка является выпадающей, ее исключают из информации и строят заново статистический ряд.

Гистограмма и полигон являются дифференциальными, а кривая накопленных опытных вероятностей – интегральным статистическими законами распределения опытных ПН (рис.1.).

Гистограмму строят следующим образом. По оси абцисс откладывают в масштабе значение ПН (длину интервала – А), а по оси ординат – частоту m_i или опытную вероятность P_i для данного i – ого интервала.

При построении i – ой точки полигона по оси ординат откладывают частоту m_i или опытную вероятность P_i , а по оси абцисс t_ic – середину данного i – ого интервала. Точкой полигона является точка пересечения ординаты с абциссой.

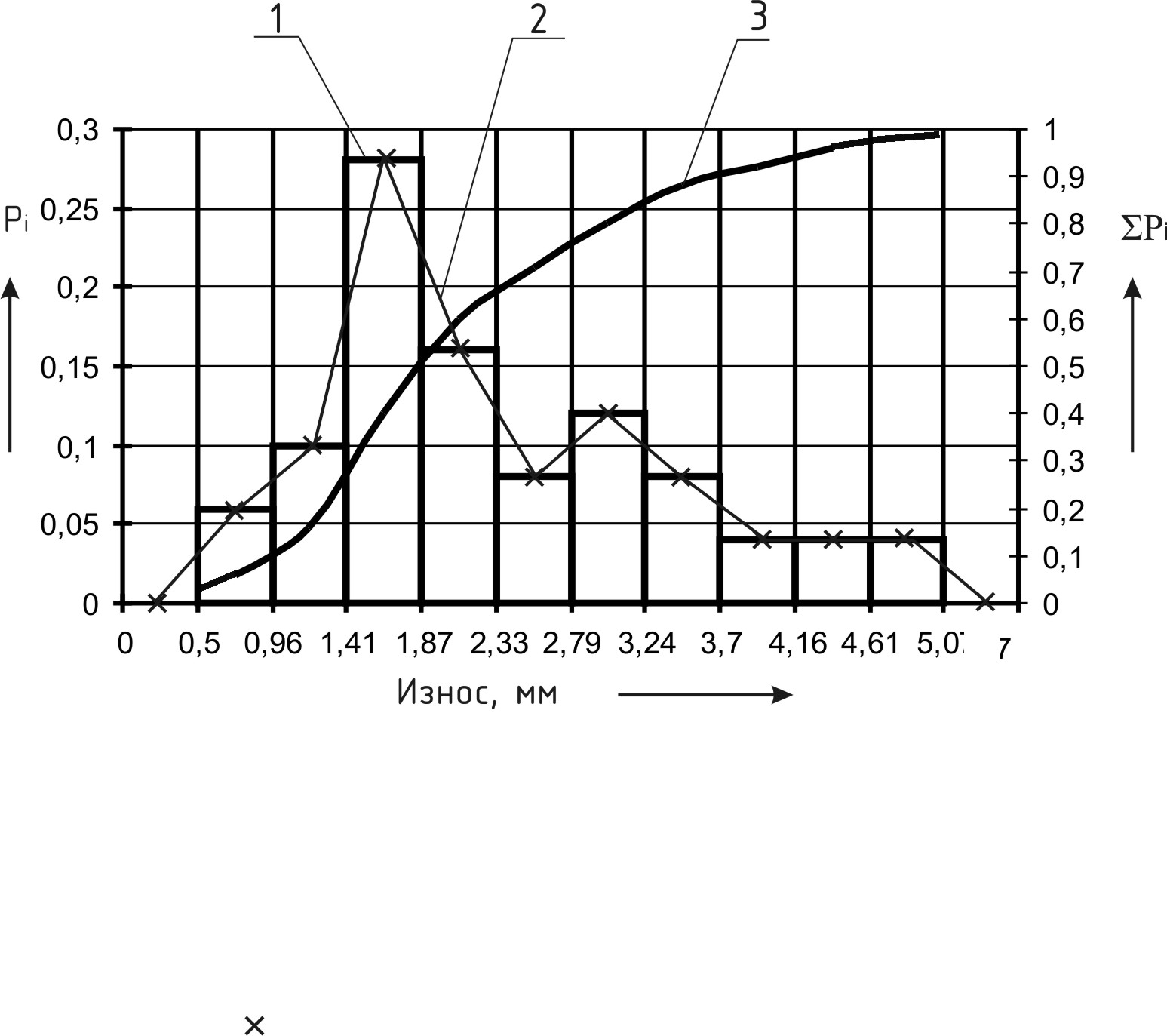
Рис. 1. Статистические законы распределения опытных показателей надежности (износ посадочного места под подшипник 7522 в вальцедековом станке СВУ-2):

1 – гистограмма; 2 – полигон; 3 – кривая накопленных опытных вероятностей

Площадь каждого прямоугольника гистограммы, площадь под полигоном в пределах интервала равны количеству объектов в долях единицы, у которых значения ПН находятся в границах этого интервала.

Начальную и конечную точки полигона получают смещением последнего по оси абцисс на половину интервала относительно начала первого и конца последнего интервалов соответственно влево и вправо.

Точку кривой накопленных опытных вероятностей в i – ом интервале получают при пересечении ординаты, равной сумме вероятностей

i – интервалов и абциссы конца данного i – ого интервала – t_iк.

Коэффициент вариации V является относительной характеристикой рассеивания ПН и используется при предварительном выборе и оценке ТЗР.

Для ПН, зона рассеивания которых начинается от нуля, коэффициент вариации V определяют по формуле

V = / ,

Если зона рассеивания смещена относительна нуля формула имеет вид

V = / ( - t _см)

При V< 0,3 предварительно выбирают закон нормального распределения (ЗНР), если V > 0,5 – закон распределения Вейбулла (ЗРВ).

Проверку совпадения опытных и теоретических законов распределения ПН производят по критериям соответствия Пирсона, Колмогорова или Стьюдента.

Критерий согласия Пирсона ² представляет собой сумму квадратов отклонений опытных и теоретических частот в каждом интервале укрупненного статистического ряда информации.

² = (m_i – m_mi)² / m_mi,

где n _y – число интервалов в укрупненном статистическом ряду;

m_i – опытная частота в i – ом интервале укрупненного статистического ряда;

m_mi – теоретическая частота в i – ом интервале укрупненного статистического ряда.

Укрупненный статистический ряд составляют исходя из условий:

n_y 4, m_i 5. Допускается объединение тех интервалов в которых m_i < 5.

После выбора количества интервалов укрупненного статистического ряда необходимо заполнить табл. 2.

Теоретическую частоту в i – ом интервале рассчитывают по формуле

m_mi =

где F(t _iк) и F(t _iн) – интегральные функции в конце и начале i – го интервала укрупненного статистического ряда.

Таблица 2. Информация об интервалах укрупненного статистического ряда

Номер i – го интервала укрупненного статистического ряда	Границы i – го интервала tiн - tiк, мм	Опытная частота i – го интервала,
1 2 … nу

Интегральную функцию ЗНР определяют по равенству

F(t _iк) = F_o

где F_o – центрированная и нормированная интегральная функция, определяемая по табл. П.2. приложения.

Следует учитывать, что

F_o(– t) = 1 – F_o (+t)

Интегральную функцию ЗРВ определяют из табл. П.3. приложения, по величине параметра ЗРВ – b и отношению (t _iк - t _см) / а, где а – параметр ЗРВ.

Параметры а и b можно приближенно рассчитать по формулам

а = , b = 1 / V^1,06. (3)

Рассчитав значения критерия согласия Пирсона ² для ЗНР и ЗРВ, по таблице П.4 приложения, определяют вероятность совпадения опытных и теоретических данных Р. Для входа в таблицу необходимо определить число степеней свободы r по формуле

r = n _y – K,

где К – число обязательных связей. Для ЗНР и ЗРВ число обязательных связей К = 3: две связи это два параметра распределения, а третья связь – = 1,0.

Вероятность совпадения является критической при Р = 10%, то есть если Р 10%, данный теоретический закон распределения непригоден. Из двух ТЗР выбирают тот, который обеспечивает большее совпадение опытных и теоретических данных.

После окончательного выбора ТЗР рассчитывают значения дифференциальной функции в серединах интервалов исходного статистического ряда f(t_ic).

Для ЗНР по известной формуле

f(t_ic) = (A / ) ,

где – центрированная дифференциальная функция ЗНР, определяемая по отношению в таблице П.5 приложения.

Следует учитывать, что f_o(– t) = f_o(+ t).

В случае ЗРВ значения дифференциальной функции в середине i – го интервала исходного статистического ряда определяют как разницу интегральных функций в конце и в начале i – го интервала статистического ряда.

f(t_ic) = F(t_ik) – F(t_iн)

Затем по полученным данным строят график дифференциальной функции (функции плотности вероятности).

На следующем этапе по таблице П.2. приложения, используя отношение , определяют значения интегральной функции ЗНР в концах интервалов исходного статистического ряда.

В случае ЗРВ значения интегральной функции в концах интервалов исходного статистического ряда определяют из таблицы П.3. приложения по параметру b и отношению (t _iк - t _см) / а. Далее по полученным данным строят график интегральной функции.

Значения характеристик показателя надежности изменяются в зависимости от условий эксплуатации машин и объема выборки. Оценивают эти изменения доверительными границами рассеивания. Определение границ рассеивания ПН и возможной ошибки их переноса является одной из основных задач теории надежности. Границы в которых может колебаться значение одиночного ПН при заданной доверительной вероятности называют нижней доверительной границей и верхней доверительной границей рассеивания . На рисунке 2.2 показана взаимосвязь между доверительной вероятностью , доверительными границами рассеивания и и возможной максимальной ошибкой е для ЗНР.

Максимальную абсолютную ошибку для одиночного ПН определяют по формуле

е = , (4)

где - коэффициент Стьюдента, определяемый по значению доверительной вероятности и объему выборки N из таблицы П. 6 приложения.

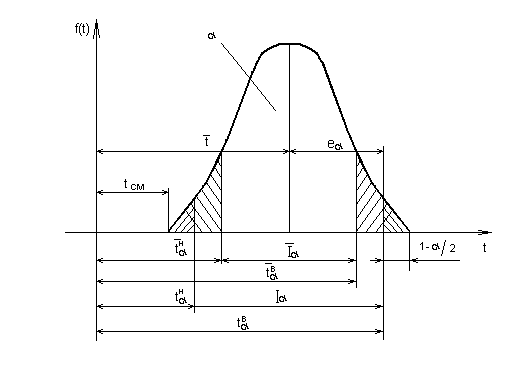
Рис. 2. Взаимосвязь между доверительной вероятностью , возможной максимальной ошибкой е , доверительными границами рассеивания одиночного ( и ) и среднего и значений ПН для ЗНР

Нижнюю и верхнюю доверительные границы рассеивания при ЗНР рассчитывают соответственно по формулам

= – е ; = + е (5)

В случае ЗРВ нижнюю и верхнюю доверительные границы рассеивания определяют соответственно по формулам

= + а , = + а ,

где – квантиль ЗРВ, определяемый по таблице П. 7 приложения по параметру b и величинам (1 – ) / 2 и (1 + ) / 2.

Интервал в который при заданной доверительной вероятности попадает 100 % от N показателей надежности, называют доверительным

интервалом I , и его определяют по формуле

I = – (6)

В практике чаще приходится определять доверительные границы рассеивания среднего значения показателя надежности.

Среднее квадратическое отклонение при этом определяют по формуле

при законе нормального распределения и заданной доверительной вероятности показатели рассеивания среднего значения показателя надежности определяют по преобразованным формулам (4), (5) и (6):

абсолютную ошибку по формуле

е =

нижнюю и верхнюю доверительные границы рассеивания по формулам

= – (е / ), = + (е / )

доверительный интервал по формуле

= -

При законе распределения Вейбулла нижнюю и верхнюю доверительные границы рассеивания определяют по формулам

= , = ,

где r₁ и r₃ – коэффициенты распределения Вейбулла, которые определяют по таблице П.6 приложения в зависимости от заданной доверительной вероятности и объема выборки N.

Доверительные границы рассеивания при законе распределения Вейбулла, в отличие от закона нормального распределения, ассиметричны среднему значению показателя надежности.

При расчете характеристик ПН и переносе их на другие группы машин той же марки необходимо оценить наибольшую возможную ошибку этого переноса. Из рис. 2. следует, что наибольшая абсолютная ошибка переноса опытных характеристик ПН при заданной доверительной вероятности будет равна е в обе стороны от среднего значения ПН – .

Относительную предельную ошибку переноса ( в процентах) независимо от ТЗР определяют по формуле

= 100( – ) / ( – )

Практическая работа № 6

Обработка усеченной и многократно усеченной информации

о надежности объекта методами вероятностной бумаги

Цель работы: Изучить методы обработки усеченной и многократно

усеченной информации о надежности объекта

Общие сведения

Определение параметров ТЗР графическими методами

Выбор точек для нанесения на вероятностную бумагу при полной,

усеченной и многократно-усеченной информации

При использовании вероятностной бумаги отпадает необходимость в расчете параметров ТЗР – , и V.

При N ≤ 10 используют все опытные точки информации, которые называют координатными точками.

При N > 10 выбирают 5 – 7 точек, равномерно расположенных в общем объеме. Накопленная опытная вероятность первой точки должна составлять ∑ P₁ = 0,08 – 0,15, а последняя является предпоследней или последней в выборке.

Накопленную вероятность координатных точек определяют по формуле

∑ P_i = № i / (N + 1), (1)

где № i – порядковый номер i – ой точки в таблице исходной информации.

В ходе наблюдений некоторые объекты могут быть приостановлены не достигнув предельного состояния (например, в связи с производственной необходимостью часть наблюдаемых тракторов передали в другое хозяйство). В этом случае информация является многократно усеченной.

При многократно-усеченной информации порядковые но­мера координатных точек с учетом приостановленных объектов (расчетные номера № i_p) определяются по уравнению

№ i_p = + (N + 1 - )/(N + 1 – N_o – N_пр), (2)

где № i_p и № i_p' – расчетные номера i – ой и предыдущей отказавших объектов;

N₀ и N_пp — соответственно количество отказавших и приостановленных объектов до № i_p.

Пример

Таблица 1. Многократно усеченная информация по межремонтным ресурсам 10 двигателей тракторов ДТ-75М (план NUT, Т = 3800 мото-ч)

Номер наблюдаемого трактора	Номер отказавшего трактора	Наработка до конца наблюдения	Наработка до очередного ремонта
1 2 3 4 5 6 7 8 9 10	1 2 3 Приостановлен 4 Приостановлен Приостановлен 5 6 Приостановлен	1550 1800 2050 2250 2400 2900 2950 3000 3250 3800	1550 1800 2050 - 2400 - - 3000 3250 -

№ 1_р = 1,0; № 2_р = 2,0; № 3_р = 3,0; № 4_р = 3,0 + (10+1-3)/(10+1-3-1) = 4,14;

№ 5_р = 4,14 + (10+1-4,14) / (10+1-4-3) = 5,85; № 6_р =

5,85 + (10+1-5,85) / (10+1-5-3) = 7,56

Соответственно по формуле (3.1) получим значения накопленных опытных вероятностей для координатных точек

∑ P₁ = 1/(10+1) = 0,09; ∑ P₂ = 1/(10+1) = 0,18; ∑ P₃ = 0,27;

∑ P_4,14 = 4,14/(10+1) = 0,38; ∑ P_5,85 = 0,53; ∑ P_7,56 = 0,69

Построение функциональной сетки вероятностной бумаги

Функциональную сетку вероятностной бумаги составляют так, чтобы нанесенная на эту бумагу интегральная функция распределения была представлена прямой. Для выпрямления интегральной функции на ось ординат наносят накопленные вероятности координатных точек ∑ P_i = 0,01; 0,05; 0,10; 0,20…0,95. При этом расстояния отметок от начала оси ординат берут равными значениям соответствующих квантилей. Значения квантилей приведены в таблицах П.7 и П.8 приложения.

Вероятностная бумага ЗНР

По оси абцисс откладывают t_i в произвольном масштабе М_х. Если t_см = 0, то t₁ = 0.

Начальная точка отсчета по оси ординат ∑ P_i = 0,01 → соответственно значение квантиля Н_к (0,01) = Н_к (0,99) = 2,326 (см. таблицу П.7). Расстояние У_i в мм координатной точки ∑ P_i от начальной точки оси ординат пропорционально разности квантилей этих координатных точек Н_к (0,01) и Н_к (∑ P_i), умноженной на масштабный коэффициент М, то есть

М[Н_к (0,01) - Н_к (∑ P_i)].

Приняв М = 50 мм и получим

У_i (мм) = 50 [2,326 - Н_к (∑ P_i)]

В виду того, что дифференциальная и интегральная функции имеют симметричную форму относительно среднего значения показателя надежности , верхняя половина оси ординат в интервале ∑ P_i = 0,5 – 0,99 будет зеркальным отражением нижней половины.

Если = 0,05, по таблице П.7 получим, что Н_к (0,05) = Н_к (0,95) = 1,645

У (∑ P_i = 0,05) = 50 (2,326 – 1,645) = 34 мм

Значения У_i ординаты в зависимости от ∑ P_i приведены в таблице П.9 приложения.

Примем масштаб по оси абцисс 1 мм = 20 мото-ч и определим координаты точек

№ 1_р = 1,0; Х₁ = 1550/20 = 77,5 мм; ∑ P₁ = 0,09; У₁ = 49,3 мм;

№ 2_р = 2,0; Х₂ = 1800/20 = 90,0 мм; ∑ P₂ = 0,18; У₂ = 70,5 мм;

№ 3_р = 3,0; Х₃ = 2050/20 = 102,5 мм; ∑ P₃ = 0,27; У₃ = 85,6 мм;

№ 4_р = 4,14; Х_4,14 = 2400/20 = 120 мм; ∑ P_4,14 = 0,38; У_4,14 = 101,0 мм

№ 5_р = 5,85; Х_5,85 = 3000/20 = 150 мм; ∑ P_5,85 = 0,53; У_5,85 = 120,1 мм

№ 6_р = 7,56; Х_7,56 = 3250/20 = 162,5 мм; ∑ P_7,56 = 0,69; У_7,56 = 141,1 мм

Интегральную прямую проводят так, чтобы количество точек с обеих сторон было примерно одинаковым, а отклонения от прямой минимальные.

Определение параметров ЗНР ( и )

При ЗНР среднему значению показателя надежности соответствует ∑ P = 0,5. Поэтому пересечение горизонтали ∑ P = 0,5, соответственно У = 116,3 мм с интегральной прямой дает абциссу А = 137 мм (рис.1.). Умножив абциссу А на масштабный коэффициент М_х получаем среднее значение показателя надежности .

= А*М,

= 137*20 = 2740 мото-ч

Среднее квадратичное отклонение определяют графическим способом на основе уравнения = ( - t_i) / Н_к (F_i). При значении квантиля Н_к (F_i) = 1 получим = - t_i. Из таблицы П.7 получаем, что квантилю Н_к (F_i) = 1 соответствует ∑ P_i = 0,16. Следовательно среднему квадратичному отклонению на графике будет соответствовать отрезок Б, представляющий разность абцисс и t_{∑ P = 0,16}.

= А*М,

= 46*20 = 920 мото-ч

Рис. 1. Графическая часть обработки усеченной информации по

закону нормального распределения

Вероятностная бумага ЗРВ

Для построения вероятностной бумаги ЗРВ по оси абцисс отмечают логарифмы текущих значений t_i в масштабе. Один порядок логарифмов

(1 … 10 или 10 … 100) принимают равным 100 мм. Абциссу (в мм) координатной точки с учетом смещения t_iсм определяют по формуле

Х_i = 100 lg (t_i – t_см)

Ординату (в мм) координатной точки с учетом масштабного фактора М = 50 определяют по формуле

У_i = 50{2,37 + [lglg 1/ (1 - ∑ P_i)]}

или по значению ∑ P_i в таблице П.10 приложения.

Определим координаты точек, приняв размерность ресурса в сотнях мото-ч.

№ 1_р = 1,0; Х₁ = 100 lg (15,5 – 13,0) = 40,0 мм; ∑ P₁ = 0,09; У₁ = 49,1 мм;

№ 2_р = 2,0; Х₂ = 100 lg (18,0 – 13,0) = 70,0 мм; ∑ P₂ = 0,18; У₂ = 65,3 мм;

№ 3_р = 3,0; Х₃ = 87,5 мм; ∑ P₃ = 0,27; У₃ = 75,3 мм;

№ 4_р = 4,14; Х_4,14 = 104,0 мм; ∑ P_4,14 = 0,38; У_4,14 = 84,4 мм

№ 5_р = 5,85; Х_5,85 = 123,0 мм; ∑ P_5,85 = 0,53; У_5,85 = 94,3 мм

№ 6_р = 7,56; Х_7,56 = 129,0 мм; ∑ P_7,56 = 0,69; У_7,56 = 103,8 мм

Определение параметров (а и b) по интегральной прямой ЗРВ

Параметр «а» определяют как антилогарифм абсциссы точки пересече­ния интегральной прямой с горизонталью ΣР = 0,63, проведенной на расстоянии 100,3 мм от оси абсцисс (рис. 2).

а = антиlg (А/100)

А = 126 мм; а = антиlg 1,26 = 18,2 сотен ч. = 1820 ч.

Рис. 2. Графическая часть обработки усеченной информации по закону распределения Вейбулла

Параметр «b» определяют как тангенс угла наклона интегральной пря­мой к оси абсцисс, с учетом выбранного масштаба

b = 200 / Б

Б = 168 мм; b = 200 / 168 = 1,2

Расчет среднего значения ПН – и, среднего квадратичного отклонения при ЗРВ

По величине параметра «b», из табли­цы П.11 приложения, определяют вспомогательные коэффици­енты К_в и С_в

Среднее квадратичное отклонение определяется по уравнению

= а* С_в

= 1820*0,79 = 1440 мото-ч

Среднее значение ПН – определяют по уравнению

= а К_в + t_см

= 1820*0,94 + 1300 = 3010 мото-ч

Окончательный выбор ТЗР производят визуально (по лучшему совпадению координатных точек с интегральной прямой) или (при незначительной визуальной разнице) по кри­терию согласия Пирсона ².

Оценка качества ремонта сельскохозяйственной техники

Для оценки качества ремонта сельскохозяйственной техники используют коэффициенты ка­чества по среднему межремонтному _мр и 90 – процентному межремонтному гамма – ресурсу К(90%)_мр

_мр = _мр (90%) / 1,45 (90%) К_з, (3)

К(90%)_мр = Т(90%) _мр / (90%) К_з, (4)

где _мр и _мр (90%) – фактические средний межремонтный ресурс и 90 % гамма-ресурс отремонтированных машин на контролируе­мом ремонтном предприятии;

(90%) – нормированный по Российской Федерации 90% гамма-ресурс;

К_з – зональный коэффициент.

В табл. 2. приведены нормированные 90% гамма-ресурсы двигателей и трансмиссии тракторов ДТ-75 и МТЗ-80, а в табл. 3. – зональные коэффициенты.

Таблица 2 . Нормированный 90% гамма-ресурс двигателей

и трансмиссии

Марка трактора	ДТ-75М	МТЗ-80
Двигатели мото-ч	1600*	3500*
Трансмиссии мото-ч	2000*	4200*

* значения нормированных 90% гамма-ресурсов двигателей и

трансмиссии тракторов в таблице 3.2 являются ориентировочными и предназначены для учебных целей

При законе нормального распределения 90 – процентному межремонтному

гамма – ресурсу Т(90%) будет соответствовать абсцисса точки пересечения инте­гральной прямой c горизонталью ΣP = 0,10, проведенной на расстоянии 52,2 мм от оси абсцисс.

_мр (90%) = В*М,

где В —длина отрезка В на рис. 1.

Таблица 3. Зональный коэффициент по регионам Российской

Федерации

Регион Российской Федерации	Зональный коэффициент*
Северо-западный Центральный Волго-Вятский Центрально-Черноземный Поволжский Северо-Кавказский Уральский Западно-Сибирский Восточно-Сибирский Дальневосточный Юго-Западный Южный	0,8 0,8 0,75 1,0 1,0 1,0 0,85 0,9 0,75 0,75 0,9 1,0

* значения зональных коэффициентов являются ориентировочными и предназначены для учебных целей

_мр (90%) = 79 * 20 = 1580 мото-ч

В случае закона распределения Вейбулла 90 – процентному межремонтному гамма – ресурсу Т(90%) будет соответствовать антилогарифм абсциссы точки пересечения ин­тегральной прямой с горизонталью ΣР = 0,10, проведенной на расстоянии 51,5 мм от оси абсцисс, суммированный с величиной смещения t_см.

_мр (90%) = антиlg 0,01 В + t_см = 10^{0,01 В} + t_см,

где В —длина отрезка В на рис. 2.

В расчете: _мр (90%) = антиlg 0,01*43 + 1300 = 100*10^0,43 + 1300 =

= 1570 мото-ч

Коэффициент качества ремонта по среднему межремонт­ному ресурсу определяют по формуле (3)

_мр = 3010 / 1,45*1600*1,0 = 1,3

Коэффициент качества ремонта по 90 – процентному межремонтному гамма-ресурсу определяют по формуле (4)

В случае ЗНР

К(90%)_мр = 1580 / 1600 = 0,99

В случае ЗРВ

К(90%)_мр = 1570 / 1600 = 0,98

Проверкой качества ремонта двигателей СМД-20 на ремонтном предприятии Южного региона установлено, что коэффициент ка­чества по среднему межремонтному _мр составляет 1,30, а коэффициент ка­чества по 90 – процентному межремонтному гамма – ресурсу К(90%)_мр составляет 0,99.

Качество ремонта двигателя можно считать хорошим.

Практическая работа № 7

Определение надёжности технических систем с последовательным,

параллельным и смешанным соединением элементов

Цель работы: изучить виды технических систем по способу соединения элементов, методику расчета надежности систем с последовательным, параллельным и смешанным соединением элементов.

Общие сведения

Система – множество элементов и связь между ними, образующие целостность.

Элемент – часть системы, предназначенная для выполнения определенных функций и неделимая на составные части при данном уровне рассмотрения.

Уровень рассмотрения определяет отнесение объекта к системе или элементу.

Например, двигатель является системой по отношению к кривошипно-шатунному механизму. В то же время по отношению к машине (трактор, комбайн или автомобиль) двигатель является элементом. Кривошипно-шатунный механизм является системой по отношению к коленчатому валу и элементом по отношению к двигателю.

Различают последовательное, параллельное и смешанное соединение элементов в системе (рис.1.).

а)

б) в)

Рис. 1. Схемы соединения элементов в системе: а) – последовательное; б) – параллельное; в) – смешанное соединение элементов в системе

Надежность системы с последовательным соединением элементов

Конструкция сельскохозяйственных машин представляет в основном систему с последовательным соединением элементов.

Вероятность безотказной работы системы с последовательным соединением элементов определяют по формуле [6]

P_s = P_i, (1)

где P_i – вероятность безотказной работы i-го элемента системы.

Как следует из формулы (1) надежность такой системы быстро убывает с увеличением количества элементов и надежность системы всегда меньше наименее надежного входящего в ее схему элемента.

Вероятность безотказной работы системы меняющейся с течением времени или наработки t рассчитывают по формуле

P_s (t) = P_i (t), (2)

где P_i (t) – вероятность безотказной работы i-го элемента системы при наработке t.

Интенсивность отказов системы

λ_s (t) = λ_i (t), (3)

где λ_i (t) – интенсивность отказов i-го элемента системы при наработке t.

Надежность системы с параллельным соединением элементов

Резервирование – применение дополнительных средств и возможностей с целью сохранения работоспособного состояния объекта при отказе одного или нескольких элементов.

При резервировании элементы в системе соединены параллельно. При этом элементы системы делят на основные и резервные.

Основной элемент – элемент, необходимый для выполнения системой требуемых функций при отсутствии отказов ее элементов.

Резервный элемент – элемент, предназначенный для выполнения функций основного элемента при отказе последнего.

Способы резервирования представлены на рис. 2.

Общее резервирование – метод повышения надежности, при котором резервируется изделие в целом.

Раздельное резервирование – метод повышения надежности, при котором резервируются отдельные части изделия.

Различают резервирование с целой и дробной кратностью.

Кратность резервирования m – отношение числа резервных элементов к числу основных.

При резервировании с целой кратностью m представляет собой целое число, в случае резервирования с дробной кратностью m есть дробное несокращаемое число. Например m = 4/2 означает резервирование с дробной кратностью, при котором число резервных элементов равно четырем, число основных – двум, а общее число элементов составляет шесть.

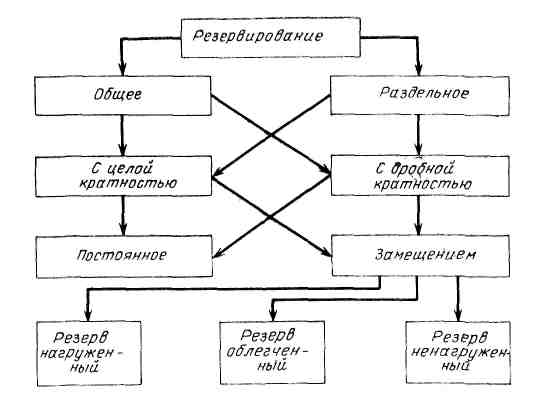
Рис. 2. Способы резервирования

По способу включения различают постоянное резервирование (нагруженный резерв) и резервирование замещением (ненагруженный резерв).

При постоянном резервировании резервные элементы подключены к основным и находятся в одинаковом с ними режиме.

При резервировании замещением резервные элементы замещают основные элементы в случае отказа последних.

До момента включения в работу резервные элементы могут находиться в трех состояниях:

- нагруженный резерв (резервный элемент воспринимает такую же нагрузку как и основной);

-облегченный резерв (резервный элемент воспринимает часть нагрузки основного элемента);

- ненагруженный резерв (резервный элемент не воспринимает нагрузку).

На рис. 3 показаны схемы различных способов резервирования.

Общее постоянное резервирование с целой кратностью

Вероятность безотказной работы системы определяют по формуле [А. М. Половко]

P_s (t) = 1 – [1 – P_i (t)]^m+1, (4)

где P_i (t) – вероятность безотказной работы i-го элемента в течение времени t; n – количество элементов в основной или резервной цепи системы; m – кратность резервирования.

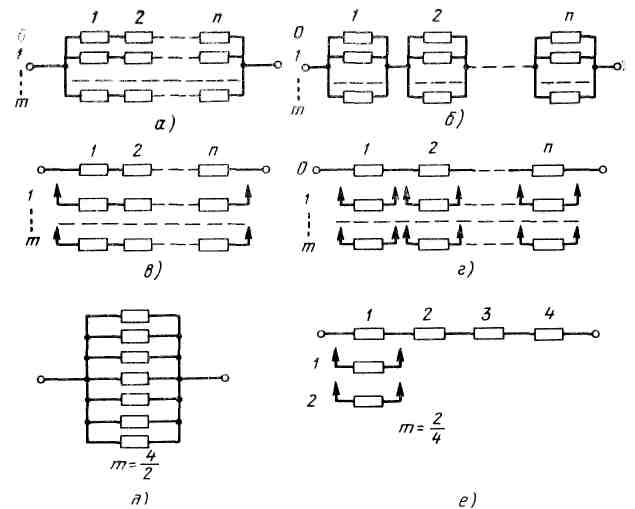
Рис. 3. Схемы различных способов резервирования: а – общее постоянное с целой кратностью; б) – раздельное постоянное с целой кратностью; в – общее замещением с целой кратностью; г – раздельное замещением с целой кратностью; д – общее постоянное с дробной кратностью; е - раздельное замещением с дробной кратностью

При экспоненциальном распределении, так как P_i (t) = е^{– (t)} вероятность безотказной работы системы

P_s (t) = 1 – [1 – е^{– λ t}]^m+1, (5)

Средняя наработка системы до отказа

_sо1 = = _о1 , (6)

где λ = λ_i (t) – интенсивность отказов системы при наработке t; _о1 – средняя наработка до отказа основной или резервной подсистем.

Если каждый элемент имеет экспоненциальное распределение наработки и одинаковую интенсивность отказов, то вероятность безотказной работы системы с одним резервным элементом (m = 1, дублирование) можно определить по формуле

P_s (t) = 2е^{– λ t} – е^{– 2λ t} (7)

Средняя наработка системы до отказа при дублировании (m = 1)

_sо1 = (8)

При резервировании неравнонадежных изделий

P_s (t) = 1 – F_i (t) = 1 – (1 – P_i (t), (9)

где F_i (t) – вероятность появления отказа в течение времени t i–го изделия.

Раздельное постоянное резервирование с целой кратностью

Вероятность безотказной работы системы определяют по формуле

P_s (t) = {1 – [1 – P_i (t)] ^{m +1}}, (10)

где P_i (t) – вероятность безотказной работы i-го элемента в течение времени t; n – количество элементов в основной цепи системы; m_i – кратность резервирования i-го элемента.

При экспоненциальном распределении, так как P_i (t) = е^{– (t)} вероятность безотказной работы системы

P_s (t) = {1 – [1 – е^{– λ t}]^{m +1}} (11)

Если элементы имеют одинаковую надежность и кратность резервирования получим

P_s (t) = {1 – [1 – е^{– λ t}]^{m +1}}ⁿ (12)

Средняя наработка системы до отказа

_sо1 = = , (13)

где к_i = (i + 1)/(m+1).

Общее резервирование с замещением (ненагруженным резервом) и целой кратностью

Система с ненагруженным резервом – система с параллельным соединением элементов, в которой в каждый момент времени работает только один элемент; если работающий элемент выходит из строя, то включается резервный элемент (резервирование замещением). На рис.4 показана схема системы с ненагруженным резервом.

Рис. 4. Схема системы с ненагруженным резервом

При экспоненциальном распределении и ненагруженном резерве вероятность безотказной работы системы

P_s (t) = е ^{– λ (t) )} (14)

Средняя наработка системы до отказа

_sо1 = _о1(m + 1), (15)

где _о1 – средняя наработка до отказа основного элемента.

При дублировании, когда в системе один резервный элемент

P_s (t) = е ^{– λ t} (1 + λ t) (16)

Если переключатель имеет отказы с интенсивностью λ_п, а элементы постоянную интенсивность λ, то для системы с дублирующим элементом (m = 1)

P_s (t) = е ^{– λ t} [1 + (1 – е ^– )] (17)

Раздельное резервирование замещением с целой кратностью

Вероятность безотказной работы системы определяют по формуле

P_s (t) = P_i (t), (18)

где P_i (t) – вероятность безотказной работы системы из-за отказов i-го элемента, резервированного по способу замещения.

Общее резервирование с дробной кратностью и постоянно включенным

резервом

Вероятность безотказной работы системы рассчитывают по формуле

P_s (t) = , (19)

_sо1 = , (20)

где P_о (t) – вероятность безотказной работы основного или любого резервного элемента; l – общее число основных и резервных подсистем; h – число подсистем, необходимых для нормальной работы резервированной системы.

Кратность резервирования в этом случае определяют по формуле

m = ( – h)/h

Скользящее резервирование

При экспоненциальном распределении вероятность безотказной работы системы определяют по формуле

P_s (t) = , (21)

_sо1 = _о1(r + 1), (22)

где λ_о – интенсивность отказов нерезервированной системы; r – число резервных элементов.

Надежность системы со смешанным соединением элементов

Вероятность безотказной работы системы со смешанным соединением элементов определяют по формуле

P_s (t) = Р(А)*Р(В), (23)

где Р(А) – вероятность безотказной работы подсистемы с последовательным соединением элементов; Р(В) – вероятность безотказной работы подсистемы с параллельным соединением элементов.

P(А) = P_i, P(В) = 1 – (1 – P_j),

где P_i – вероятность безотказной работы i-го элемента подсистемы с последовательным соединением n – элементов; P_j – вероятность безотказной работы j-го элемента подсистемы с последовательным соединением g – элементов.

Ход работы

Пример 1. Дана система, схема расчета надежно­сти которой изображена на рис. 5. Необходимо найти вероятность безотказной работы системы при известных вероятностях безотказной работы ее элементов (значе­ния вероятностей указаны на рисунке).

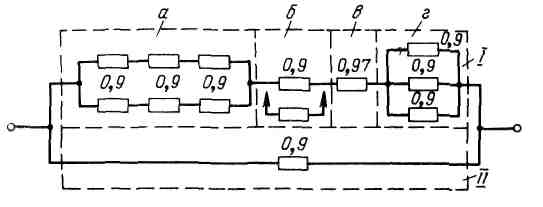
Рис. 5. Схема соединения элементов в системе

Решение: Из рис. 5. видно, что система состоит из двух (I и II) неравнонадежных устройств.

Устройство I состоит из четырех узлов:

а – дублированного узла с постоянно включенным резервом, причем каждая часть узла состоит из трех последовательно соединенных (в смысле надежности) элементов расчета;

б – дублированного узла по способу замещения;

в – узла с одним нерезервированным элементом;

г – резервированного узла с кратностью т = 1 / 2 (схе­ма группирования).

Устройство II представляет собой нерезервированное устройство, надежность которого известна.

Так как оба устройства неравнонадежны, то на осно­вании формулы (9) имеем

Найдем вероятность p_I(t). Вероятность безотказной работы устройства I равна произведению вероятностей безотказной работы всех узлов, т. е. p_I = p_aр_бр_вp_г.

В узле а число элементов основной и резервной цепи n = 3, а кратность резервирования т = 1. Тогда на осно­вании формулы (4)

В узле б кратность общего резервирования замещением т = 1, тогда на основании формулы (16) имеем

В узле г применено резервирование с дробной крат­ностью, когда общее число основных и резервных систем l = 3, число систем, необходимых для нормальной работы, n = 2. Тогда на основании формулы (19)

Вероятность безотказной работы устройства I будет

Тогда вероятность безотказной работы резервированной системы будет

Пример 2. Вероятность безотказной работы преобразователя постоянного тока в переменный в течение t = 1000 час равна 0,95, т. е. Р (1000) =0,95. Для повышения надежности системы электроснабжения на объекте имеется такой же преобразователь, который включа­ется в работу при отказе первого. Требуется рассчитать вероятность безотказной работы и среднюю наработку до первого отказа системы, состоящей из двух преобра­зователей.

Решение: Из условия задачи видно, что имеет ме­сто общее резервирование с замещением при кратности т = 1. Тогда на основании формулы (16) имеем

Из условия задачи = 0,95, тогда λ₀t = 0,05. Подставляя значения P (1000) и полученное значение λ₀t в выражение для P_c(t), получим

Средняя наработка до первого отказа системы на основании формулы (15) будет

Пример 3. Схема расчета надежности устройства приведена на рис. 6. Предполагается, что последействие отказов отсутствует и все элементы расчета равно-надежны. Интенсивность отказов элемента λ = 1,35 · 10^-3 1/час. Требуется определить наработку до первого отказа резервированного устройства.

Рис. 6. Схема соединения элементов в системе

Решение: Имеет место раздельное резервирование равнонадежных устройств с постоянно включенным резервом. Для вычисления средней нара­ботки до первого отказа целесообразно воспользоваться формулой (13). По условию задачи число элементов не­резервированной системы n = 2, .кратность резервирова­ния т = 1. Тогда

Задачи для СРС

Задача 1. Схема расчета надежности приведена на рис. 7. Необходимо найти вероятность безотказной работы изделия, если известны вероятности отказов элементов.

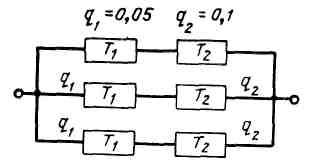
Рис. 7. Схема соединения элементов в системе

Ответ: Р_s = 0,997

Задача 2. Схема расчета надежности показана на рис. 8, где приведены данные о вероятностях безотказной работы элементов. Определить вероятность безотказной работы Р_s и вероятность отказа F_s изделия.

Рис. 8. Схема соединения элементов в системе

Ответ: Р_s = 0,991; F_s = 0,009.

Задача 3. Схема расчета надежности показана на рис. 9. Определить по известным вероятностям отказов элементов q₁ и q₂ вероятность безотказной работы изделия.

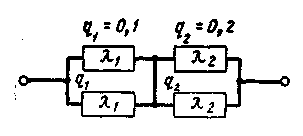
Рис. 9. Схема соединения элементов в системе

Ответ: Р_s = 0,95.

Задача 4. Схема расчета надежности показана на рис. 10, на кото­ром приведены вероятности безотказной работы элементов. Вычислить вероятность безотказной работы изделия.

Рис. 10. Схема соединения элементов в системе

Ответ: Р_s = 0,997.

Задача 5. Схема расчета надежности показана на рис. 11. Интенсив­ности отказов элементов имеют следующие значения: λ₁ = 0,3 · 10^-3 l/час, λ₂ = 0,7 · 10^-3 1/час. Необходимо определить вероятность безотказной работы изделия в течение времени t = 100 час, среднюю наработку до первого отказа, частоту отказов и интенсив­ность отказов в момент времени t = 100 час.

Рис. 11. Схема соединения элементов в системе

Ответ: Р_s = 0,99; _sо1 = 1500 ч; f_s(100) = 1,8*10^-4 1/ч; λ_s (100) = 1,8*10^-4 1/ч.

Задача 6. Схема расчета надежности изделия показана на рис. 12. Интенсивности отказов элементов имеют значения: λ₁ = 0,3 · 10^-3 l/час, λ₂ = 0,7 · 10^-3 1/час. Требуется найти вероятность безотказной работы изделия в течение времени t =100 час, среднюю наработку до первого отказа, частоту отказов и интенсивность отказов в момент времени t = 100 час.

Рис. 12. Схема соединения элементов в системе

Ответ: Р_s (100) = 0,994; _sо1 = 1760 ч; f_s(100) = λ_s (100) = 0,108*10^-3 1/ч.

Задача 7. Схема расчета надежности изделия приведена на рис. 13. Вероятность безотказной работы нерезервированного устройства в течение 300 час равна 0,74, резерв ненагруженный и интенсивность отказов устройств λ = const. Необходимо найти его вероятность и среднее время безотказной работы

Рис. 13. Схема соединения элементов в системе

Ответ: Р_s (300) = 0,995; _sо1 = 3000 ч.

Задача 8. Предложено конструктором три варианта схем построения изделия (рис. 14):

а) изделие нерезервировано и средние наработки до первого отказа элементов равны T₁ = T₂ = 300 час;

б) один элемент дублируется путем замещения при ненагруженном состоянии резерва, а второй, как и в схеме рис. 14, а, нерезервирован, причем средние наработки до первого отказа дублированного узла и нерезервированного элемента те же;

в) один элемент дублирован путем постоянно включенного резерва, а второй нерезервирован, причем, как и в схемах рис. 14, а и б, средние наработки до первого отказа дублированного узла и нерезервированного элемента равны 300 час.

Какой из вариантов более предпочтителен с точки зрения надеж­ности, если надежность изделия оценивать средней наработкой до первого отказа?

Рис. 14. Схема соединения элементов в системе

Ответ: Т_а = 150час, Т_б = 167 ч; Т_в = 165 ч.

Задача 9. Система состоит из двух одинаковых элементов. Для повышения ее надежности конструктор предложил два следующих варианта (рис. 15): а – дублирование системы по способу замещения с ненагруженным состоянием резерва; б – скользящее резерви­рование при одном резервном элементе, находящемся в ненагруженном состоянии. Какой из вариантов более целесообразен с точки зрения надежности, если интенсивность отказов элемента λ?

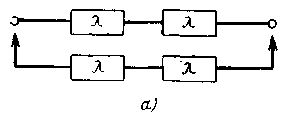
Рис. 15. Схема соединения элементов в системе

Задача 10. Схема расчета надежности изделия приведена на рис. 7. Требуется определить интенсивность отказов изделия при t =100 час, если интенсивности отказов элементов имеют следующие значения: λ₁ = 0,23 · 10^-3 l/час, λ₂ = 0,17 · 10^-3 1/час.

Ответ: λ_s (100) = 19,2*10^-7 1/ч.

Задача 11. Схема расчета надежности изделия приведена на рис. 16. Вероятность безотказной работы элементов составляет: Р₁ = 0,7; Р₂ = 0,9; Р₃ = 0,8. Определить вероятность безотказной работы системы со смешанным соединением элементов.

Рис. 16. Схема соединения элементов в системе

Ответ: P_s = 0,78.

Список литературы

1. Надежность и ремонт машин. Методические указания / А. И.Сидоров, А. Н. Батищев, В. З. Бубнов – М.: ВСХИЗО, 1987 – 65 с.

2. Кравченко И. Н., Зорин В. А., Пучин Е. А., Бондарева Г. И. Основы надежности машин: Учебное пособие для вузов. Часть 1. – М.: Изд-во, 2007. – 224 с.

3. Надежность и ремонт машин. В. В. Курчаткин, Н. Ф. Тельнов, К. А. Ачкасов, В. И. Савченко и др. / Под ред. В. В. Курчаткина. – М.: Колос, 2000.

4. А. И. Селиванов, Ю. Н. Артемьев. Теоретические основы ремонта и надежности сельскохозяйственной техники. М.: Колос, 1978. – 248 с.

5. Жиркин Ю. В. Надежность, эксплуатация и ремонт металлургических машин: Учебник. – Магнитогорск: МГТУ, 2002. – 330 с.