4.4. Определение эмпирических закономерностей

Разнообразные способы получения информации о закономерностях, присущих тому или иному объекту исследования, можно разделить на две группы.

Наблюдения, когда исследователь не вмешивается в ход наблюдаемого процесса, ограничиваясь упорядоченной регистрацией значений интересующих его величин.

Эксперимент, когда ход процесса и регистрируемые значения величины зависят от последовательности изменений некоторых других величин, задаваемой исследователем (т.е. исследователь активно вмешивается в ход процесса).

Каждая группа способов имеет свои достоинства и недостатки. Введение искусственных изменений переменных, влияющих на состояние объектов исследования, позволяет целенаправленно и быстро получить искомые зависимости между переменными. Однако для того чтобы исследуемый эффект достаточно отчетливо проявился на фоне различных шумов, могут требоваться значительные изменения переменных. Для многих промышленных объектов это оказывается невозможным, поскольку такой эксперимент может привести к недопустимому по технологическим условиям режиму и даже к аварийным ситуациям. Кроме того, чтобы исключить при проведении опытов непредусмотренные режимы, значения неизменяемых переменных должны быть стабилизированы. Только при выполнении данного условия отдельные опыты обладают достаточной воспроизводимостью, а результаты достоверны. Требуемую стабильность неизменяемых переменных сравнительно легко можно обеспечить на лабораторных и полупромышленных установках. В производственных же условиях добиться стабильности весьма сложно, а во многих случаях невозможно. Например, для производств, где перерабатывается природное сырье, изменение переменных процесса не зависит от желания экспериментатора. Именно в этом случае применяется метод наблюдений, при использовании которого экспериментатор вынужден ожидать проявления интересующих его закономерностей, что значительно удлиняет время экспериментирования. Надо также иметь в виду, что описания, полученные на основании результатов наблюдений, справедливы лишь для имевшего место диапазона изменений переменных и, следовательно, носят частный характер.

Таким образом, метод проведения активного эксперимента предпочтителен. Однако в условиях плохой воспроизводимости опыта практически единственно возможным является метод наблюдений.

Успех применения экспериментальных методов тем более ощутим, чем выше уровень теоретических знаний об исследуемом объекте. В то же время следует отметить, что эмпирические методы в ряде случаев позволяют получить некоторое теоретическое представление о механизме исследуемого процесса и практически оценить теоретические предпосылки, имеющие часто односторонний, субъективный характер.

Не останавливаясь подробно на экспериментальных методах исследования, следует отметить некоторые из них [15,7]. На практике часто возникает задача определения влияния на состояние объекта исследования (конструкция, технологический процесс) факторов, имеющих только качественную оценку или не поддающиеся измерению, например, при выяснении влияния различных свойств сырья на качество изделий. Решение подобных задач составляет предмет дисперсионного анализа.

Если объект исследования по технологическим, техническим или экономическим соображениям не допускает преднамеренного варьирования входных переменных в необходимом диапазоне, то для накопления статистического материала применяется пассивный эксперимент, заключающийся в наблюдении и регистрации значений входных и выходных переменных в режиме нормального функционирования исследуемого объекта.

Выбор структуры модели является наиболее неформализуемой процедурой эксперимента, так как исследователь до начала эксперимента, как правило, не располагает необходимой априорной информацией.

Построение модели существенно упрощается, если в качестве ее составляющих используются полиномы, которые следует включать в уравнение регрессии. Модели полиномиального вида имеют преимущество в связи с тем, что с их помощью аналитическая функция (4.14) может быть описана достаточно точно.

(4.14)

Но прежде чем приступить к проведению эксперимента, необходимо выделить наиболее существенные входные величины (факторы) из всей совокупности входных величин, оценить степень корреляции между ними и исключить из числа подлежащих регистрации те из них, которые сильно коррелированны с другими. Выделение наиболее существенных входных переменных производят, например, методом априорного ранжирования [7, 16].

Как известно, любую функцию, если она не имеет бесконечных разрывов, можно разложить в степенной ряд Тейлора. Поэтому в теории эксперимента чаще всего математическое описание представляется в виде полинома путем разложения в ряд Тейлора:

, (4.15)

где b₀, b_j, b_ij, b_jj – постоянные коэффициенты уравнения, оценки которых необходимо определить в результате постановки и проведения эксперимента; п – число наиболее существенных входных величин, полученных в результате отсеивающего эксперимента [16, 17].

Параметр b_о функции (4.15) называется свободным членом уравнения; b_j – линейными эффектами; b_ij – эффектами парного взаимодействия; b_jj – квадратичными эффектами и т.п. Чем больше параметров модели (4.15), тем больше опытов придется провести.

Сначала целесообразно рассматривать простейшую и линейную модель

(4.16)

Если объект исследования (конструкция, технологический процесс) допускает целенаправленное изменение всех наиболее существенных входных переменных (факторов) по заранее определенным образом составленной программе в требуемых диапазонах варьирования, то применяется однофакторный или многофакторный активный эксперимент для построения математической модели объекта [16, 17].

Факторами называют наиболее существенные входные величины, принимающие в некоторый момент времени определенное значение. Область определения фактора, т.е. совокупность всех значений, которые принимает данный фактор, может быть непрерывной и дискретной. В задачах планирования активного эксперимента всегда используются дискретные области определения, а для факторов с непрерывной областью определения (температура, сила, время и т.п.) выбираются дискретные множества уровней. Кроме того фактор должен быть управляемым (поддерживаемым постоянным в течение опыта или меняющимся по заданной программе), однозначным (не являющимся функцией других факторов), измеряемым с достаточно высокой точностью. В совокупности факторы должны быть совместимы (их комбинации осуществимы и безопасны), между ними не должно быть линейной корреляции [16].

Факторы, как правило, имеют различную физическую природу и размерность, а опыты нередко проводятся только на двух уровнях факторов x_Hj и x_Bj. Для упрощения обработки результатов эксперимента уровни факторов нормализуются, т.е. центрируются и нормализуются. За нулевой (начальный, основной) принимается уровень x_0j, соответствующий середине интервала [x_Hj, x_Bj]:

(4.17)

Точка факторного пространства с координатами х₀₁, х₀₂, …, х_0k называется центром плана. На рис. 4.6 показано расположение центра плана (х₀₁, х₀₂) при двух факторах.

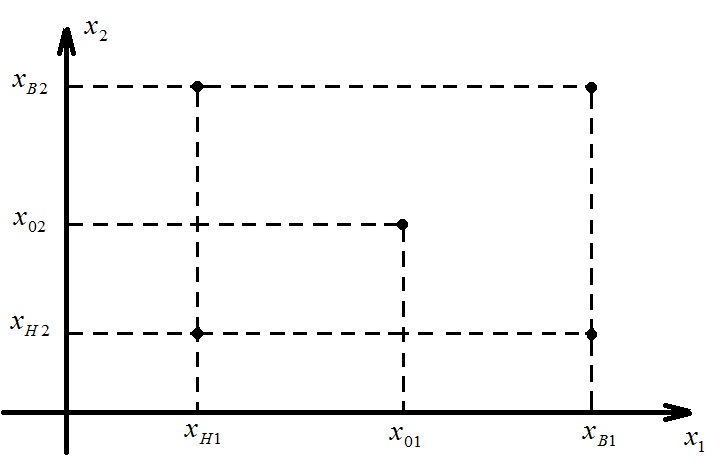
Рис. 4.6 Расположение центра плана при двух факторах

Если для каждого фактора выбрать интервал варьирования

(4.18)

то прибавление Δx_j к нулевому уровню дает верхний уровень x_Bj, а вычитание – нижний уровень x_Hj фактора. Линейное преобразование

(4.19)

переменных х₁, х₂, …, х_k дает возможность перейти к новой системе координат , в которой функция (4.15) принимает вид:

(4.20)

При значениях фактора уровни исходных факторов становятся равными x_Bj и x_Hj соответственно. Следовательно, для всех безразмерных и нормированных факторов в новой системе координат верхний уровень равен +1, нижний равен -1, а координаты центра плана равны нулю и совпадают с началом координат (рис. 4.7).

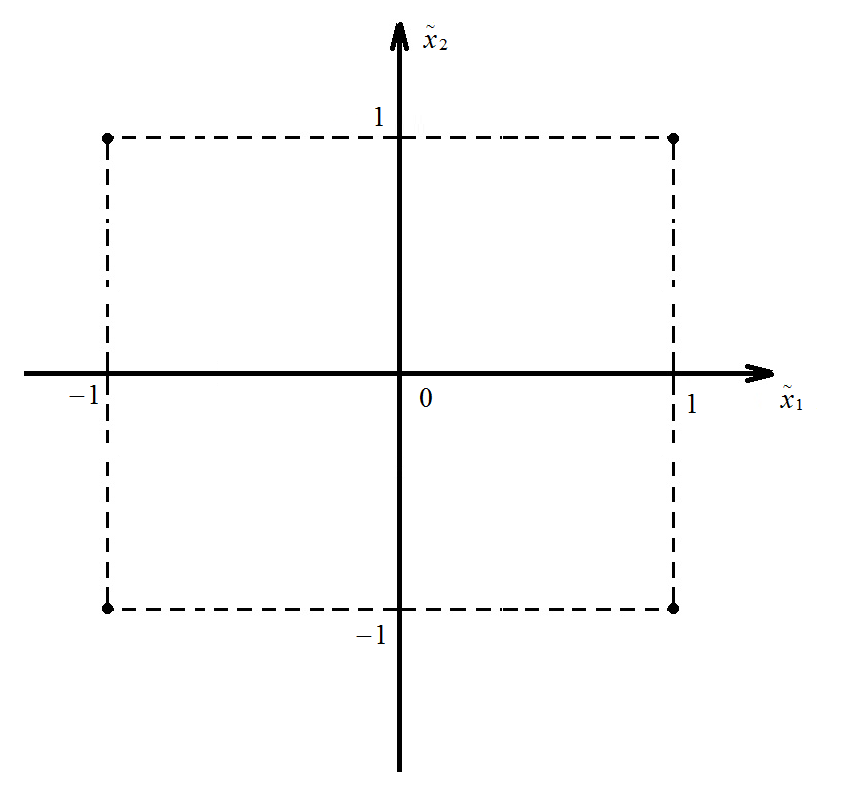
Рис. 4.7 Новая система координат

Геометрически нормализация факторов равноценна линейному преобразованию пространства факторов, при котором производится перенос начала координат в точку, отвечающую основным уровням, и сжатие-растяжение пространства в направлении координатных осей. Нормализация переменных существенно упрощает построение математической модели объекта. После построения модели с нормированными факторами и её оценки можно вернуться к многочлену (4.15) с натуральными факторами, используя нормирующие соотношения

(4.21)

В плане полного факторного эксперимента (ПФЭ) реализуются все возможные сочетания уровней факторов [18]. Если при k факторах опыты проводятся только на двух уровнях, то необходимое количество опытов N = 2^k. Такой план используется только при небольшом количестве факторов (k ≤ 5) и называется ПФЭ 2^k. Исходные данные для всех факторов записываются в таблицу (табл. 4.3).

Таблица 4.3

Уровень	Фактор
	x1	x2	…	xk
xHj
xBj

План эксперимента можно описать с помощью специальной таблицы (матрицы), в которой каждая строка соответствует условиям одного опыта. В табл. 4.4 приведен план эксперимента при двух факторах.

Таблица 4.4

Номер опыта	Фактор, отклик
				у
1	+	+	+	у1
2	+	−	+	у2
3	+	+	−	у3
4	+	−	−	у4

Результаты опытов записываются в последнем столбце табл. 4.4. Для вычисления свободного параметра а₀ в таблицу добавлен столбец фиктивной переменной , всегда равный +1. В таблице пишутся только знаки уровней . В первом опыте оба фактора находятся на верхнем уровне, т.е. и . Во втором опыте значения и и т.д.

При трех факторах в плане ПФЭ 2³ необходимо провести восемь опытов. В таблице опытов этого эксперимента (табл. 4.5) дважды повторяется план ПФЭ 2², сначала при значении , а затем при .

Аналогично при любом количестве факторов k необходимо дважды повторить план для случая k − 1 (сначала при значении k-го фактора на верхнем уровне, а затем на нижнем). В таблице 4.5 показано последовательное достраивание таблицы плана ПФЭ при увеличении k от 2 до 4.

Нормированное значение j-го фактора в опыте с номером i обозначается через .

Вычисление неизвестных параметров функции (4.28) осуществляется методом наименьших квадратов. Согласно этому методу параметры должны быть выбраны так, чтобы достигалось наименьшее значение функции

Таблица 4.5

План			Номер опыта						у
		22	1	+	+	+	+	+	у1
			2	+	−	+	+	+	у2
			3	+	+	−	+	+	у3
			4	+	−	−	+	+	у4
	23		5	+	+	+	−	+	у5
			6	+	−	+	−	+	у6
			7	+	+	−	−	+	у7
			8	+	+	−	−	+	у8
24			9	+	+	+	+	−	у9
			10	+	−	+	+	−	у10
			11	+	+	−	+	−	у11
			12	+	−	−	+	−	у12
			13	+	+	+	−	−	у13
			14	+	−	+	−	−	у14
			15	+	+	−	−	−	у15
			16	+	−	−	−	−	у16

, (4.22)

где - значения отклика и факторов (приведенные в табл. 4.5) в опыте с номером i.

Рассмотрим сначала линейную модель

(4.23)

В методе наименьших квадратов параметры a_j вычисляются [16, 17] по единой формуле

(4.24)

В тех случаях, когда эффект фактора х_j зависит от уровня, на котором находится другой фактор х_i , имеет место взаимодействие двух факторов х_ji , для оценки которого вводят в матрицу планирования столбец произведений этих факторов.

Поскольку изменение выходной переменной носит случайный характер, то эксперимент проводится с m параллельными опытами и определяется среднее значение выходной переменной по каждой строке матрицы планирования y_g (g = ).

Чтобы исключить влияние систематических ошибок, вызванных наличием помех, используется случайная последовательность при постановке опытов, запланированных матрицей, т.е. опыты рандомизируются во времени. Выбранную по таблице случайных чисел последовательность [16] не рекомендуется нарушать.

Число опытов в ПФЭ значительно превосходит число определяемых коэффициентов модели, что приводит к большой избыточности опытов. Кроме того, с помощью ПФЭ можно получить только либо линейную, либо неполноквадратическую математическую модель, так как из полного факторного эксперимента нельзя извлечь информацию о квадратичных членах полинома (4.15).

В первом случае избыточность опытов используют для формирования планов дробного факторного эксперимента (ДФЭ), а во втором – при необходимости переходят к планам более высокого порядка, например композиционным планам второго порядка, в которых используются принципы ортагональности и ротатабельности планирования.

На основе полученных в процессе эксперимента закономерностей [19, 20] нередко решаются задачи синтеза конструкций и технологических процессов, носящих оптимизационный характер [21, 22]. Они направлены на выбор варианта, обеспечивающего наилучшие технико-экономические показатели.

Наиболее распространенными являются следующие задачи оптимизации [15]:

• без ограничений: , где х = (х₁, …, х_j , …, х_n) – вектор оптимизируемых параметров; - целевая функция, формализующая связь между технико-экономическими показателями и оптимизируемыми параметрами. Для ее решения используются классические методы поиска экстремума или интерактивные поисковые алгоритмы;

• математического программирования , где - множество допустимых решений. Если целевая функция и функции, описывающие ограничения, линейные, то для решения используются методы линейного программирования, при нелинейном характере целевой функции и ограничений – методы нелинейного программирования. Этот вид задач наиболее часто встречается при конструировании и разработке технологии;

• экстремальные задачи в условиях неопределенности характеризуются неопределенностями в описании случайных воздействий на конструкцию и технологические процессы, множества ограничений в выборе целевой функции. Для их решения используются стохастические методы оптимизации.