4.3. Методы оценки результатов измерений

Погрешности результата измерения физической величины дают представление о том, какие цифры в его числовом значении являются сомнительными. Поэтому нет смысла выражать погрешность результата измерения большим числом цифр. Достаточно ограничиться одной значащей цифрой или двумя, если вторая является пятеркой. Две значащие цифры удерживаются в числовых значениях погрешности только при ответственных и точных измерениях.

Округлять числовое значение результата измерения следует [10] в соответствии с числовым разрядом значащей цифры погрешности, т.е. числовое значение результата измерения должно оканчиваться цифрой того же разряда, что и значение погрешности.

График, как средство анализа ряда результатов наблюдений

Результаты ряда наблюдений одной и той же величины представляют собой набор отличающихся друг от друга чисел. Разница между результатами наблюдений, остающаяся после исключения систематических погрешностей, объясняется наличием случайных погрешностей. В первоначальном виде такой ряд можно оценить только очень приближенно, т.е. установить, велик ли разброс погрешностей. Уловить же какой-либо закономерности этого ряда на глаз по числам очень трудно. Дальнейшая математическая обработка с использованием приемов, описанных далее, позволяет характеризовать случайные погрешности.

Однако при математической обработке исчезает один признак ряда результатов измерений – их последовательность. Теория случайных погрешностей построена на предположении, что каждое единичное измерение самостоятельно и не зависит от других, а следовательно, не зависит от их последовательности [10].

В действительности, отказываясь от фактора последовательности, уравнивая правомерность каждого единичного измерения, мы лишается возможности оценивать некоторые характерные особенности всего ряда, в частности, степени наблюдения, указания об одинаковой тщательности наблюдений, неизменности условий измерений и т.п. Выявлению этих особенностей может помочь графическое изображение ряда результатов наблюдений в их реальной последовательности.

Графики целесообразно строить до начала математической обработки результатов измерений. Они дают основание для решения вопроса о пригодности полученного ряда для математической обработки.

В процессе измерения появляются грубые погрешности – это погрешности, не характерные для процесса или технологии, приводящие к явным искажениям результатов измерения. При оценке грубых промахов приходится прибегать к обычным методам проверки статистических гипотез.

Проверяемая гипотеза состоит из утверждений, что результат измерений не содержит грубой погрешности, а является одним из значений случайной величины. Обычно проверяют наибольшее и наименьшее значения результатов измерений. Для проверки гипотез используются следующие критерии [12, 13]:

Если число измерений , то может быть использован критерий Шовине. В этом случае грубой ошибкой (промахом) считается результат , если разность превышает значения , определяемые в зависимости от числа измерений:

,

где – СКО, полученное по формуле (4.12).

2. Критерий Романовского, используемый при числе измерений . При этом вычисляют отношение

и полученное значение сравнивают с теоретическим при выбираемом уровне значимости (см. табл. 4.2). Уровень значимости – это вероятность отвергнуть верную гипотезу при статистической проверке гипотезы. Обычно при обработке результатов измерений её значение принимают в пределах 0,05…0,1.

Таблица 4.2

Уровень значимости q	Число измерений n
	4	6	8	10	12	15	20
0,01	1,73	2,16	2,43	2,62	2,75	2,90	3,08
0,02	1,72	2,13	2,37	2,54	2,66	2,80	2,96
0,05	1,71	2,10	2,27	2,41	2,52	2,64	2,78
0,10	1,69	2,00	2,17	2,29	2,39	2,49	2,62

Если β≥β_т, то результат х_i считается промахом и отбрасывается.

3. Критерий трёх сигм (3σ) – наиболее распространенный (σ≈S). Он используется, когда количество измерений n≥20…50. В этом случае считается, что результат, полученный с вероятностью Р = 0,003, маловероятен и его можно квалифицировать как промах. Т.е. сомнительный результат x_i должен быть исключен из измерений, если

.

Методы проверки нормального закона распределения случайных величин. При статистической обработке результатов измерений особую роль играет проверка соответствия распределения случайных величин нормальному закону, которому чаще всего подчиняются результаты большинства случайных измерений, что необходимо для обоснованного выбора доверительных границ результатов измерений и оценки точности измерений [14]. В наибольшей степени этой цели соответствует критерий (критерий Пирсона) – хи квадрат.

Для этой цели необходимо количество измерений 40 и более.

Обычно принимается следующий порядок решения задачи [14].

Диапазон полученных результатов измерений делят на r интервалов шириной Δx_i (i = 1, 2, …, r).

Для каждого интервала подсчитывают частоты m_{i ,} равные количеству результатов, лежащие в каждом i-м интервале.

Определяют частоту появления величины в каждом интервале:

,

где n – количество измерений, индекс «*» означает статистическую оценку.

Находят оценку средней плотности распределения случайной величины x_i в каждом интервале Δx_i :

.

Строят гистограмму распределения величины x_i , откладывая по оси абсцисс результаты наблюдений в виде интервалов Δx_i в порядке возрастания индекса i, а по оси ординат – оценку средней плотности распределения , получая прямоугольник с высотой .

Естественно, что площадь всех построенных прямоугольников равна единице, поскольку в нее входят все 100% наблюдений:

.

При построении гистограммы число интервалов r выбирают в зависимости от числа измерений n, исходя из соотношений: при n = 40…100 r = 7…9, а при n = 100…500, r = 8…12, а масштабы по осям гистограммы рекомендуется принимать такими, чтобы отношение ее высоты к основанию составляло 5 : 8 (рис. 4.5).

Соединяя середины отрезков, получают полигон распределения. Характер ломаной линии позволяет сделать предположение о виде распределения, что дает возможность с большей долей вероятности подобрать соответствующую кривую распределения.

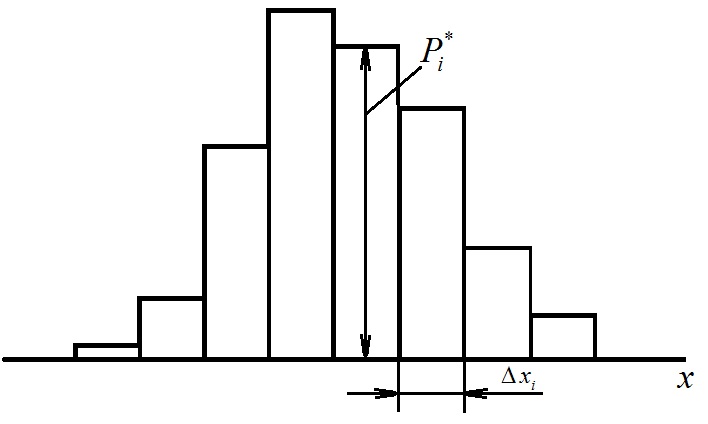
Рис. 4.5 Полигон и гистограмма распределения

Если СКО и математическое ожидание полигона распределения близки к значению СКО и математическому ожиданию кривой нормального распределения, то этот вид распределения можно положить в основу гипотезы о правомерности такого предположения.

Поскольку предположение основано на результатах опытных данных случайных величин, оно должно быть подтверждено обычными методами математической статистики по критериям согласия. При числе наблюдений более 40 рекомендуется принимать критерий согласия χ² - Пирсона.