Ряд распределения

				…
				…

Еще одной, более удобной, универсальной и часто применяемой на практике формой описания закона распределения случайной величины является функция распределения , которая определяет вероятность того, что случайная величина будет принимать значения, меньшие некоторого ограничения

(4.5)

Функция распределения – это неубывающая функция, при при График функции распределения непрерывной случайной величины представлен на рис. 4.1, а дискретной – на рис. 4.2.

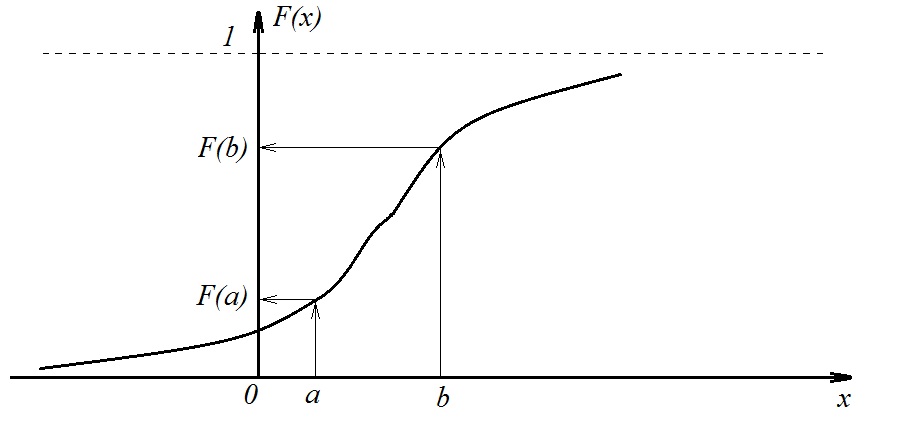
Рис. 4.1. График функции распределения непрерывной случайной величины

Функция распределения дискретной случайной имеет вид:

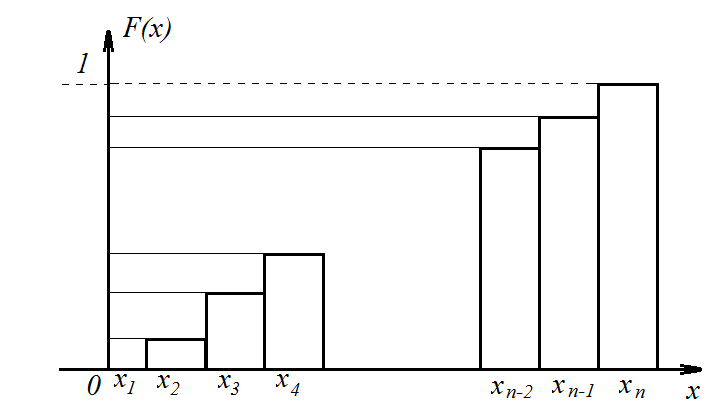
Рис. 4.2. График функции распределения дискретной случайной величины

Так как функция распределения непрерывной случайной величины (см. рис. 4.1) является непрерывно дифференцируемой, то для ее описания часто пользуются первой производной* , или плотностью распределения. Плотность распределения представляет собой одну из форм описания закона распределения, применяемых для непрерывных случайных величин. Плотность распределения обозначается, как правило, или . График плотности распределения представлен на рис. 4.3.

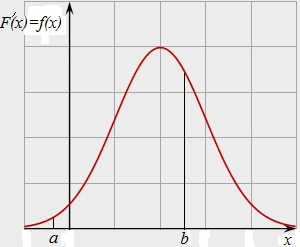
Рис. 4.3. График плотности распределения непрерывной случайной величины

Взаимосвязь между функцией распределения и плотностью распределения случайной непрерывной величины имеет вид:

(4.6)

Поскольку функция распределения – функция неубывающая (см. рис. 4.1), то плотность распределения есть функция неотрицательная, т.е. кривая распределения лежит выше оси абсцисс (см. рис. 4.3). Граничные значения функции распределения: .

Поэтому справедливо равенство:

(4.7)

Из зависимости (4.7) следует, что площадь, ограниченная кривой плотности распределения и осью абсцисс в интервале значения , равна единице. Вероятность того, что значение случайной величины принадлежит интервалу значений , равна разности значений функции распределения на границах этого интервала (см. рис. 4.1):

(4.8)

или площади под кривой плотности распределения, опирающейся на этот интервал (см. рис. 4.3).

Величина площади рассчитывается по зависимости:

(4.9)

Законы распределения позволяют решать любые практические задачи, связанные со случайными величинами, и в этом их безусловное достоинство. Наибольшее удобство для практического использования предоставляют числовые характеристики случайной величины – математическое ожидание и дисперсия случайной величины, которые характеризуют значение случайной величины и ее разброс соответственно.

Математическое ожидание случайной величины характеризует положение некоторого среднего значения случайной величины возле которого группируются возможные её значения.

Значение случайной величины x может быть определено величиной среднего арифметического значения, полученного по результатам многократных наблюдений этой величины.

(4.10)

Легко представить случай, когда для двух рядов измерений средние арифметические значения равны. Значит, одного этого значения недостаточно, чтобы охарактеризовать случайную величину. Необходима характеристика разброса. В качестве ее можно принять разность значений , полученных при измерениях результатов. Эта характеристика получила название размаха значений случайной величины.

Однако при равенстве и средних арифметических значений, и размахов два ряда измерений будут отличаться степенью группирования (концентрации) полученных результатов, например, относительно среднего арифметического значения. Подходящей характеристикой, позволяющей индивидуализировать разброс результатов многократных измерений, является суммирование величины их отклонений от среднего арифметического значения. Эта характеристика получила название дисперсии случайной величины . По определению дисперсия случайной величины – это математическое ожидание квадрата соответствующего отклонения случайной величины от ее математического ожидания :

Дисперсия случайной величины имеет размерность квадрата размерности собственной величины, что затрудняет использование дисперсии в практике метрологических работ. Поэтому в метрологии чаще используется понятие «среднее квадратическое отклонение» S(х), которое принимается равным положительному корню квадратному из значения дисперсии (При приближенных вычислениях среднее квадратическое отклонение обозначают через вместо (сигма)):

(4.11)

Вычисление на практике производится при ряде допущений. Во-первых, принимается, что . Правильнее было бы , и это приближение тем грубее, чем меньше значений получено при измерениях. Во-вторых, принимается, что . Правильнее было бы . Подобные допущения приводят к тому, что расчетные значения численных характеристик смещены относительно своих действительных значений. Поэтому в практике метрологических работ, как правило, для определения среднего квадратического отклонения применяется формула вида:

, при (4.12)

Корректировка знаменателя в зависимости (4.12) позволяет компенсировать приведенные выше допущения за счет увеличения значения . При большом числе измерений ( ) корректировка знаменателя не сказывается на величине ; при малом – имеет большое значение, причем тем больше, чем меньше .

Форма кривой плотности распределения (см. рис 4.3) отражает вид функции . Во многих характерных случаях эти функции исследованы и результатами этих исследований пользуются на практике. Среди наиболее часто употребляемых распределений прежде всего необходимо выделить так называемое нормальное распределение, или распределение Гаусса. Это обусловлено тем, что если случайная величина представляет собой сумму трех и более составляющих, то ее распределение, независимо от формы распределения слагаемых, описывается уравнением:

(4.13)

Максимум функции достигается в точке (математическое ожидание случайной величины) и равен . С возрастанием нормальная кривая становится более пологой, т.е. прижимается к оси и растягивается вдоль неё. При уменьшении нормальная кривая стягивается к прямой . Точка называется центром распределения вероятностей, или центром распределения.

График функции нормального распределения представлен на рис. 4.4.

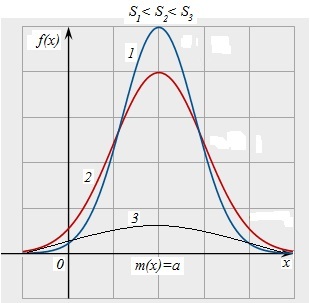
Рис. 4.4. График функции распределения нормального закона

В связи с тем, что большинство процессов измерений характеризуются большим числом составляющих погрешности измерения и это предоставляет право без проведения каких бы то ни было исследований принять для случайной погрешности нормальное распределение, нормальный закон стандартизован и является одной из двух установленных в нормативной документации форм законов распределения, применяемых при обработке результатов многократных измерений.