11

Министерство образования и науки, молодёжи и спорта Украины

ОДЕССКАЯ НАЦИОНАЛЬНАЯ МОРСКАЯ АКАДЕМИЯ

Кафедра физики и химии

Лабораторная работа № 1.8

ИССЛЕДОВАНИЕ ЗАВИСИМОСТИ ЛОБОВОГО СОПРОТИВЛЕНИЯ ОТ ФОРМЫ ТЕЛА

(Указания к лабораторной работе)

Составил проф. Михайленко В.И.

Утверждено на заседании кафедры, протокол № 2 от 29 сентября 2011 г.

Одесса - 2011

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1.1. ОСНОВНЫЕ ПОНЯТИЯ ГИДРОДИНАМИКИ. УРАВНЕНИЕ НЕРАЗРЫВНОСТИ

Гидродинамика – раздел механики, в котором изучается движение жидких и газообразных сред.

Движение жидкостей и газов называется течением.

Рассмотрим основные закономерности течения идеальной жидкости.

Идеальной называется несжимаемая жидкость, в которой отсутствуют силы вязкости (силы внутреннего трения).

Стационарным называется такое течение, скорость которого в любой точке пространства, занятого средой, остается постоянной во времени.

Различают два вида течений жидкости – ламинарное и турбулентное. Ламинарным называется течение, в котором поток жидкости представляет собой систему слоев, скользящих друг относительно друга без перемешивания. При турбулентном течении в жидкости образуются круговые потоки (вихри), которые приводят к перемешиванию отдельных слоев. Ламинарный режим течения наблюдается при малых скоростях; при повышении скорости течение становится турбулентным.

Линиями тока называются линии, касательные к которым совпадают с направлением скорости течения среды в точке касания (рис. 1). При стационарном течении линии тока совпадают с траекторией движения частиц среды и остаются неизменными во времени. Часть жидкости, ограниченной линиями тока, называют трубкой тока.

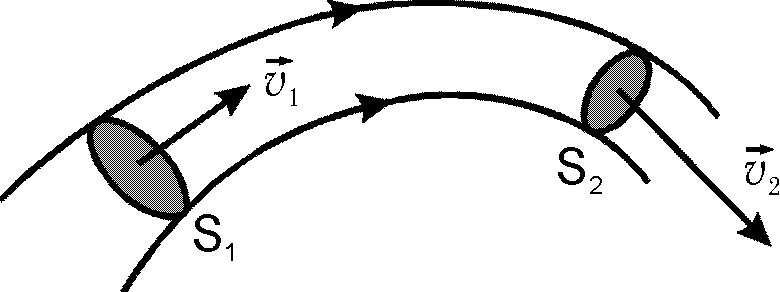
Выберем два каких-либо сечения и в трубке тока (рис. 2). За время через сечение пройдет объем жидкости . За это же время через сечение пройдет объем .Если жидкость несжимаема, то объемы и равны, поэтому

Рис. 1 Рис. 2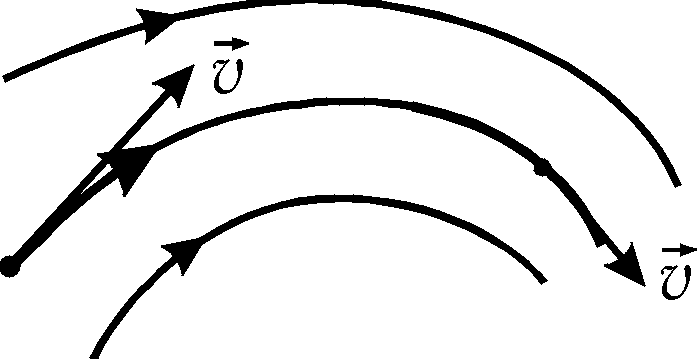

.

(1.1)

Выражение (1.1) называется уравнением неразрывности потока: произведение скорости течения на сечение трубки тока есть величина постоянная для данной трубки тока.

1.2. Уравнение бернулли

Рис. 3.

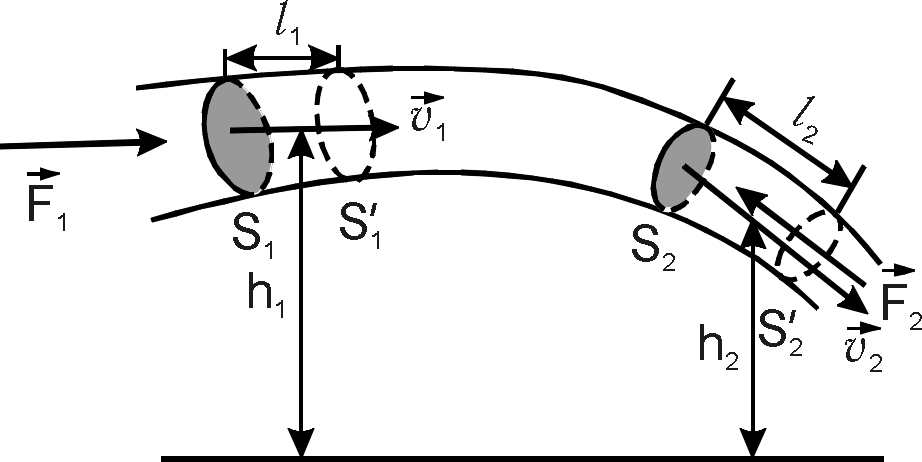
Выделим в стационарно текущей идеальной жидкости трубку тока, ограниченную сечениями и (рис. 3). Обозначим – внешнее давление, – высота, на которой расположено сечение . Аналогично в месте расположения сечения соответствующие величины имеют значения .

Спустя некоторый промежуток времени участок трубки тока займет новое положение .

Полная энергия жидкости изменится на величину . При этом масса, заключенная в объеме не меняет своего положения в пространстве, поэтому в разности нужно учесть лишь массу жидкости, заключенную в объеме или .

По закону сохранения энергии изменение энергии обусловлено работой внешних сил по перемещению жидкости массой :

.

(1.2)

При перемещении массы на расстояние выполняется работа , а на расстояние l₂ (рис. 3) , поэтому суммарная работа

Выразим силы давления и через соответствующие внешние давления и и сечения и : ; .

В итоге

,

(1.3)

где , – объемы жидкости, ограниченные сечениями и соответственно. Знак "минус" в формуле (1.3) указывает, что сила направлена навстречу силе .

Полная энергия массы жидкости равна сумме кинетической и потенциальной энергий

	(1.4)
	(1.5)

Подставив (1.3-1.5) в (1.2), получим:

.

(1.6)

В силу условия неразрывности струи , поэтому, разделив на объем и заметив, что – плотность жидкости, из (1.6) получим

или

.

(1.7)

Здесь – соответственно статическое, гидростатическое и гидродинамическое давление.

Уравнение (1.7) называется уравнением Бернулли (1738 г.): СУММА СТАТИЧЕСКОГО, ГИДРОСТАТИЧЕСКОГО И ГИДРОДИНАМИЧЕСКО­ГО ДАВЛЕНИЙ В УСТАНОВИВШЕМСЯ ПОТОКЕ ИДЕАЛЬНОЙ ЖИДКОСТИ ЕСТЬ ВЕЛИЧИНА ПОСТОЯННАЯ.

Для горизонтального потока уравнение Бернулли упрощается

(1.8)

Из уравнения (1.8) вытекает важное следствие: при увеличении гидродинамического давления статическое давление уменьшается, и наоборот. Это следствие лежит в основе одного из правил судовождения, запрещающего близко расположенным судам двигаться параллельным курсом, поскольку при этом может произойти их столкновение.

1.3. Трубка пито

Уравнение Бернулли (1.8) лежит в основе действия трубки Пито – устройства для измерения скоростей течения водных и воздушных потоков, а также относительных скоростей движения судов и самолетов.

Рис. 4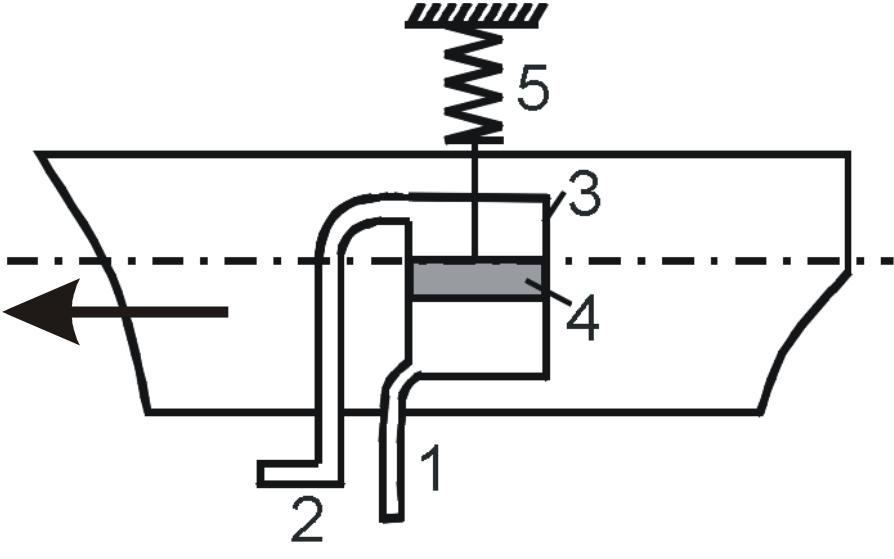

Рассмотрим конструкцию судового лага, основной частью которого является трубка Пито, представляющая собой систему из двух параллельных трубок 1 и 2, выведенных за борт судна (рис. 4). Отверстие трубки 1 направлено перпендикулярно потоку жидкости, а трубки 2 - параллельно потоку. Давление, создаваемое в трубке 2, равно сумме статического и гидродинамического давлений , а в трубке 1 действует только статическое давление .

Трубки 1 и 2 подведены к цилиндру 3, разделенному поршнем 4 на две полости. Разность давлений, действующих на поршень 4, уравновешивается пружиной 5. С помощью следящей системы перемещение штока поршня передается на ходовой мостик и другие помещения судна. Уравнение равновесия сил, действующих на поршень, имеет вид:

,

(1.9)

где – площадь поршня, – жесткость пружины, – перемещение поршня.

Из уравнения (1.9) легко найти формулу для вычисления скорости судна

.

(1.10)