3. Метод наискорейшего спуска

Метод наискорейшего спуска предложен американскими специалистами Дж. Боксом и К. Уилсоном как синтез лучших свойств градиентного метода и метода релаксации.

Недостатком градиентного метода заключается в том, что на каждом шаге надо вычислять все производные функции и определять направление градиента, что при большом числе переменных эта трудоемкая операция. Метод релаксации в том смысле обладает определенным достоинством, так как при движении вдоль выбранного осевого направления не требует вычислений производных после каждого шага. Однако в данном случае движение происходит не в оптимальном направлении, поскольку градиент в общем случае не совпадает с осевым направлением.

Метод наискорейшего спуска (крутого восхождения) сочетает основные идеи методов релаксации и градиента и заключается в следующем. Так же как в градиентном методе, в начальной точке определяет направление градиента и перемещается в этом (при поиске максимума) или в противоположном (при поиске минимума) направлении. Однако перемещаются не на один шаг, а несколько шагов (как в методе релаксации). После каждого шага оценивается только величина критерия , производные не вычисляются (рис. 3.8)

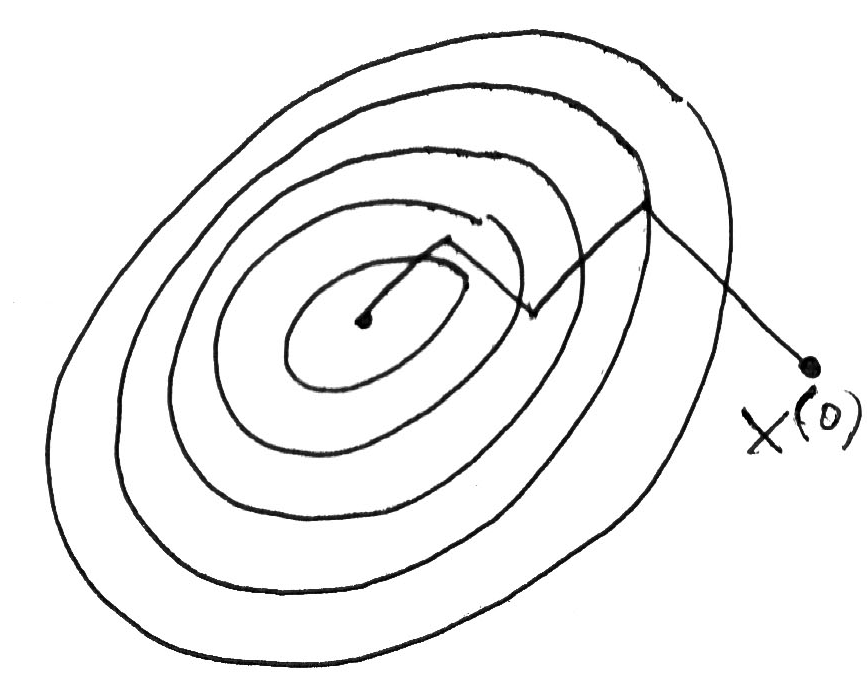
Рисунок 3.9 – Траектория движения к оптимуму в методе наискорейшего спуска

, , (3.18)

где – вектор точки, в которой последний раз вычислялся градиент .

В алгоритме (3.18) знак “+” – принимается при поиске максимума, а знак “-” – при поиске минимума. В направлении градиента выполняют шаги пока выполняется условие (при поиске минимума)

(3.19)

При нарушении условия (3.19) в последней точке определяют новое направление градиента и процедуру поиска повторяют.

Критерием окончания поиска может служить одно из условий (6,14) – (6,17) градиентного спуска.

Рассмотрим возможность улучшения алгоритма поиска Итерационный поиск (6.18) в векторной форме в точке имеет вид

(3.20)

С учетом этого можно определить значение в точке :

(3.21)

Поскольку и определены, то значение целевой функции в следующей точке

оказывается функцией только одного параметра – шага спуска (рис. 6.9). Применяя какой-нибудь метод однометрической оптимизации определяем величину оптимального шага

и координаты новой точки

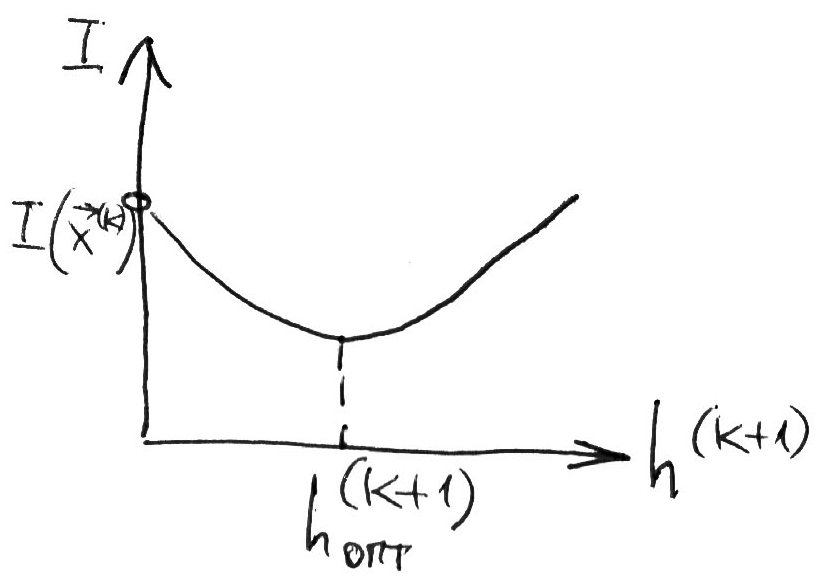
Рисунок 3.10 – Характер зависимости целевой функции от величины шага поиска

Аналогично находим:

Вычислив в новой точке градиент , имеем

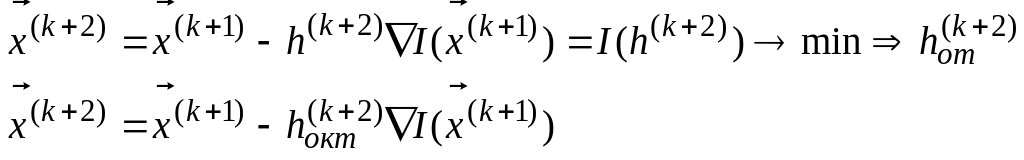
Эта процедура повторяется до выполнения одного из условий (3.14) – (3.17)

Заметим, что центральным звеном рассматриваемого алгоритма является поиск минимума функции одной переменной, что существенно увеличивает быстродействие алгоритма поиска оптимума методом наискорейшего спуска.

Этот метод, также как и другие методы градиентного спуска, определяет локальный минимум функции . Это связано с зависимостью всего пути спуска . Для определения других локальных минимумов необходимо производить поиск из других начальных точек.